基于线网滤波组合逼近法的公交通行效率提升研究——以成都市二环高架BRT为例

崔红卫， 曾 鹦， 陈 蛇

(1．西南财经大学 经济数学学院，四川 成都 611130;2．成都市社会科学院，四川 成都 610023)

基于线网滤波组合逼近法的公交通行效率提升研究
——以成都市二环高架BRT为例

崔红卫1， 曾 鹦2， 陈 蛇2

(1．西南财经大学 经济数学学院，四川 成都 611130;2．成都市社会科学院，四川 成都 610023)

针对高峰值多峰公交线路因配车多且发车频率高所引发的线路运转效率相对低下等问题，本文提出滤波组合逼近法，旨在优化公交线网以提升城市公交通行效率。借助IC卡、RFID技术、图像识别等现代信息技术，以及OD客流调查，获取高峰值多峰公交线路的站点客运量值，采用Matlab多项式曲线拟合真实客流数据获取客流量函数。通过滤波消除多峰高峰值站点，综合运用数据挖掘技术对高峰值多峰公交线路站点客运量与原线路实现魏尔斯特拉斯逼近。最后以成都市二环高架BRT为例，验证和测度滤波组合逼近法对BRT线网提档升级的可操作性和高效性，据此提出既能保证原线路客流的全覆盖，还能减少换乘次数、降低发车频次等切实可行的线网优化举措。

通行能力;滤波组合逼近法;交通诱导;RFID技术

1 引言

作为城市经济发展的“动脉”，城市公交是联系社会生产、流通和人民生活的纽带，更是城市功能正常运转的基础支撑和提升城市综合竞争力的关键承载。优先发展城市公交是缓解城市交通拥堵、治理城市雾霾和促进城市可持续发展的有效途径［1～4］。那么，如何提高公共交通的客运能力与服务质量，以保持现有的公交用户与吸引其他更多的出行者选择公交出行是提升公交出行分担率最根本和最有效的措施［5］。优化线网作为城市公交规划中最重要的一环，因其投资少、见效快且相对易于实施，近年来已引起众多学者的关注和重视［6～12］。公交线网优化的核心在于结合现有道路网布局及公交OD需求矩阵，运用交通规划理论及计算机模拟仿真等方法确定线网的合理布局，优化组合公交运力以充分发挥公交系统的最佳效益［13，14］。为实现运营者与乘客期望的社会成本最小化和社会效益最大化，学者们基于“逐步设计，优化成网”理念从空间、时间和价值等不同维度，以线网日均满载率最大［15，16］、公交乘客的总出行时间最小化［17］、用户费用和运营者费用最小［18］和直达客流密度最大［19］等目标所建立的公交线网优化模型，均用特定函数抽象表示线网优化的目标及约束条件，将复杂系统、复杂对象的决策思维过程系统化、模型化和数量化是这类方法的优势所在，这为本文研究提供了许多宝贵经验，但因理论性过强且在实践优化过程中操作性较差而导致难以对所得理论结果给出明确的解释，甚至可能存在严重的资源浪费现象。更重要的是，在模型的求解上仍有需要深入研究之处:一是关于优化模型的求解大多采用启发式算法，往往是针对单一目标进行优化，很难兼顾其他优化目标，尤其是很难满足线路重复系数和网络覆盖率等要求，尽管也有运用加权方法对多目标进行处理，但权重的确定有待进一步研究;二是因求解变量过多，为达全局最优，需反复测算各参数，求解计算量大。

综上，本文针对公交线路因早晚高峰时段客流的高峰值多峰现象造成的配车多且发车频率高而引发的线路运转效率低下等问题，提出公交线网滤波组合逼近法，旨在优化公交线网以提升城市公交通行效率:理论上证明通过多项式平滑滤波来消除多峰高峰值站点可行，实践中对客流极大值站点进行OD抽样调查，决定是否通过有效措施剔除该站点为高峰值站点;并以成都市二环高架BRT为例，测度和验证该方法对BRT线网提档升级的可操作性和高效性:采用Matlab多项式曲线拟合真实客流分布，通过滤波消除多峰高峰值站点，综合运用数据挖掘技术对高峰值多峰公交线路站点的客运需求量与原线路实现魏尔斯特拉斯逼近，据此提出既能保证原线路客流的全覆盖，还能减少换乘次数、降低发车频次等切实可行的线网优化举措。

2 线网滤波组合逼近法

公交线路的配车数和发车频率是评价线网优化与否的两个关键指标，也是公交营运生产服务的关键管理点。

2．1 高峰值多峰函数的相关概念

定义1 公交线路站点客运量。公交线路站点客运量是指在特定的营运日，特定公交线路各站点的载客量yi(i=1，2，…，n)，有(1)和(2)式成立。

其中yi为第i站点的载客量，Δyi为第i站点的净上客量，ui为第i站点的上客量，di为第i站点的下客量。ui、di(i=1，2，…，n)取值可通过人工计数或现代传感器技术等方式获得，通过(1)式和(2)式即可测出yi。随着IC卡、RFID技术、图像识别技术在现代公交的推广应用，yi值也可直接获取［20］。

定义2 公交线路站点客运量函数。公交线路站点客运量函数是指对于特定公交线路l∈L，其站点x∈X的客运量变化规律，用函数y=fl(x)表示。

其中l∈L，且L={l1，l2，…，lm}为m条公交线路集合;X={xi|i=1，2，…，n}为特定公交线路l的n个站点集合;y={yi|i=1，2，…，n}为第i站点的载客量集合。

以线路站点为自变量x，其取值为1，2，…，n，站点客运量为因变量y，运用Matlab多项式曲线拟合可获取y=fl(x)的函数关系式。

考虑到城市公交客流的动态诱导对提升城市公交优质文明服务有着积极的意义，此时y的取值为客运需求量)y更能反应真实的客流情况，)yi通过(3)式计算。

其中wi表示因车辆安全容量限制而导致第 i个(i=1，2，…，n)站点的未上客量，此处假定乘客若不能搭乘第一辆到达的车辆，则一定能够搭乘上第二辆到达的车辆，即不考虑二次等待。

定义3 高峰值多峰线路。若fl(x)在其定义域中存在多个极值，则称公交线路l为多峰线路。

通常情况下，城市公交线路多为多峰线路。对于线路过长、站点过多的多峰公交线路，其峰值往往存在以下情况:(1)存在2个以上不直接相连的站点xi，xj(i≠j，且|i－j|≠1)，点(xi，yi)和(xj，yj)为极值点;(2)当特定公交线路的满载量为y*时，若至少有线路站点xi，xj(i≠j，且|i－j|≠1)，使得客流量满足min{yi，yj}＞115y*时，这类城市公交线路为高峰值多峰线路。

2．2 函数fl(x)的多项式平滑滤波

(1)公交线网优化与线路配车

公交资源配置的关键在于满足乘客高峰期出行可接受的时间约束，并以此决定公交发车频率p*，一般地，p*=3分钟。对于给定的线路长度s公里，平均运行速度v公里/小时，所需配车量Q可通过(4)式计算。

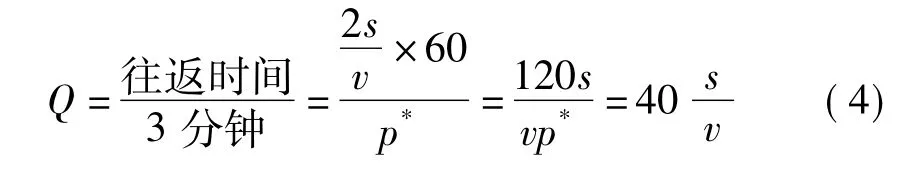
由(4)式可知，不考虑乘客等待情况，公交线路的配车数不仅与线路长度有关，还与线路运行速度有关。在公交线网优化实践中，分拆线路往往可减少配车。如sAC=18公里，vAC=12公里/小时，sCB=12公里，vCB=15公里/小时，受AC间运行速度的影响，车辆沿着ACB行驶比BCA更节约运行时间，这是因为BCA是一种“前拥后堵”的交通现象，瓶颈路段速度决定了整条线路的速度，公交配车却应按照BCA运行情形加以考虑。根据配车公式计算所得配车量为100辆。

若通过优化分拆公交线网，将线路ACB分拆为AC和CB两条线路，通过公交线路无缝换乘加以解决CB线路的公交出行问题。根据(4)式可计算AC和CB配车量分别为60辆和32辆。可见，通过优化分拆公交线网可节约公交配车8辆。

(2)消除多峰高峰值站点的滤波方法

公交运行速度会影响线路配车，是公交营运成本管控的重要方面。然而，公交乘客的上下车速度会直接影响公交线路的运行速度，该情况在客流高峰值站点更为突出。消除公交线路高峰值站点是提高公交运营效率的有效举措。

第1步 统计高峰值多峰公交线路各站点的上下客量，计算出途经各站点的载客量。

第2步 绘制高峰值多峰函数的系列图像。以站点为横坐标，分别绘制以载客量、上客量、下客量为纵坐标的函数图像。

第3步 重点研究以上客量或下客量为纵坐标的函数图像的极大值站点的客流规律，对极大值站点客流进行OD抽样调查，研究其客流的流向一致性，决定是否通过有效措施剔除该站点为高峰值站点，如新开或优化线路，使经该站点原上下客的乘客能够直接前往出行目的地，以减少大客流在该站点的换乘，以此达到降频、去峰值之目的。

第4步 线网优化效果检验。一是对拟开行或优化线路的生产条件进行评估;二是模拟检验新开或优化后线路与原线路相比，是否实现了降频或降峰值的目的;三是评估优化后的线网组合是否对原线路客流进行全覆盖;四是对客流和配车的增减进行评估，实现资源的高效利用，详见图1。

图1 线网优化效果检验

2．3 滤波组合函数的魏尔斯特拉斯有效逼近

(1)魏尔斯特拉斯逼近定理

设f(x)是［a，b］上的连续函数，对于任意 ε＞0，总存在多项式函数p(x)，使得

一般来说，不必要将f(x)展开成一个幂级数，但总可以找到一个多项式p(x)，使得对一切x∈［a，b］，f(x)与p(x)之差比预先给定的任意正数都小，即存在多项式p(x)按要求逼近f(x)。

(2)公交线路的调整

假设原公交线路l的客运量函数为fl(x)，通过降频、降峰值的优化调整，形成公交线路网络{l1，l2，…，ln}，使公交线路网络{l1，l2，…，ln}全覆盖原公交线路 l的客流。其客运函数分别为gli(x)，i=1，2，…，n，若对于任意ε＞0，对 x∈X，总有则称函数魏尔斯特拉斯逼近fl(x)。

(3)公交线路调整的优化分析

确定运用滤波组合函数的魏尔斯特拉斯有效逼近的公交线路调整优化的判断标准，详见表1。

表1 公交线路优化判断的“三降”标准

3 算例分析

本文选取成都市二环高架BRT-K2线路早高峰时段(2016年8月23日早7∶30到2016年8月23日早9∶00)的运行来检验和测度线网滤波组合逼近法对BRT线网优化的可行性和有效性。

3．1 成都市二环高架BRT简介

成都市二环高架BRT以快速路为依托，通过设置公交专用道形成快速公交系统，于2013年5月31日正式建成通车，包含K1/K2两条主线和K1A/K2A两条循环线(线路编号K1为二环高架内侧环状线路，沿顺时针方向运营;K2为二环高架外侧环状线路，沿逆时针方向运营)。

3．2 K2线的客运规律

(1)K2线站点客运量

借助二环高架BRT-K2线的进出站闸机数据统计，根据实地客流调查并结合数据分析结果可知，尽管BRT具有运量大、速度快等优势，但仍存在明显的高峰值多峰现象:红牌楼东站为换乘最大值站点，换乘客流集中前往高新南区;成仁公交站和营门口北也为换乘极值站点，换乘客流集中前往火车东站和火车北站。需要指出的是，分别以年、月、天及早高峰时段(7∶30-9∶00)为单位对K2线客流量进行的统计分析结果均支持以上结论。

(2)K2线站点客运量函数

由于早高峰各站点的客流峰值是影响公交配车数最为关键的因素，鉴于客流需求量更能反应真实的客流情况，故此处选取 K2线早高峰时段(7∶30～9∶00)的某时点客流需求量进行分析，运用Matlab多项式曲线拟合方法对基础数据进行拟合，同时获取f(K2)(x)的函数关系式，见(5)式。

其中p1=0．0000011355，p2=－0．00011197，p3= 0．0043791，p4=－0．087513，p5=0．97171，p6=－6．121，p7=23．52，p8=22．015。

f(K2)(x)为典型的高峰值多峰函数，K2线有进一步优化调整的空间，解决配车多且发车频率高而引发线路运转效率低下等问题。

3．3 K2线的优化调整

(1)重构二环路逆时针公交线网体系

成都市规划实施“三环十六射”快速路网改造，通过科华南路、杉板桥快速射线，二环路BRT乘客不经换乘通往高新南区的新世纪会展中心和火车东站，以此消除红牌楼东、高笋塘、营门口北、成仁和万年场等站点的高峰值问题。具体而言，根据快速路网条件和客流OD规律，新开行6条BRT线路，保留原K1、K2环线，形成以二环路为依托，三条快速射线为补充的快速公交路网体系，详见表2。

表2 以二环路为依托的8条BRT线路

图2 二环BRT-K2线优化前后客运函数对比

(2)二环路逆时针公交线网体系的站点客运量函数组合

优化后二环路逆时针快速公交路网体系为{K2'，K4'，K6'，K8'}，对K2线载客量的站点进行数据挖掘，根据K2线路OD调查规律进行数据模拟分配，形成BRT-K2线优化前后的客运函数对比图，如图2所示。优化后的路网体系{K2'，K4'，K6'，K8'}较K2线而言，实现了公交线网的滤波和降峰值的目的。

(3)二环路逆时针公交线网体系的魏尔斯特拉斯逼近

对优化后的路网体系{K2'，K4'，K6'，K8'}运用Matlab进行多项式曲线拟合获取客运量需求函数，见(6)式至(9)式。

其中p41=－0．0012838，p42=0．047345，p43=－0．69342，p44=5．1544，p45=－20．796，p46=45．719，p47=－49．407，p48=30。

其中p81=0．079966，p82=－5．8048，p83=140．86，p84=－1049．2。由图2可知，应根据站点x所属不同站点区段进行分段测算和验证，详见(10)式。

从严格意义上来讲，原线路K2和优化线路K2'，K4'，K6'，K8'的客运量函数 f(K2)(x)与若能精确表达，对于 ε ＞0，满足但该状态为理想状态下的收敛，(5)式至(10)式均通过Matlab多项式曲线拟合获取，尽管拟合精度较高，仍存在一定误差，故可给定一个可接受的容忍水平ψ(ψ 0，其值视具体情况而定)，对于 x∈［1，

3．4 二环BRT吸引圈线网优化后的效果测度

(1)吸引快速公交沿线乘客选乘BRT线路

在确保K2线站点和走向不变的前提下，新开行如表2所示的BRT线路，即形成以二环快速公交专用道为依托的快速公交路网。优化之后的线网，由于行车公里数和发车班次的增加、BRT吸引圈的扩大，再加上BRT本身具备的速度快、大容量优势及其客流的规模效益，可确保在不损失原有客流的同时还能吸引沿线的其他市民选乘BRT，这样一来，二环路BRT上的总客流经模拟测算约为45万人次，远超当前25万人次的日均客流量。

(2)降低K2发车密度，提高运行效率

通过对成都公交集团的调研可知，K2线路在高峰时段的发车频率为20秒，全线长度sK2=28．3km，发车830班次。根据测算，新开线路在二环高架快速公交道上的投影长度分别为sK4'=10．4km，sK6'= 11．6km，sK8'=6．3km，此时s=28．3×830=23489公里。基于滤波组合逼近法，经模拟测算K2'、K4'、K6'和K8'的发车班次分别为204、187、222和165，此时s'=11332．7公里，Q'=778，即s＞＞s'，Q Q'。可见，基于滤波组合逼近的线网优化方法有效剔除高峰值站点，据此新开或优化线路，在确保全覆盖原有线路客流的同时，还能有效节约行车公里数，降低配车成本，提高公交运行效率。

(3)减少乘客的换乘次数，提高公交吸引力

维持K2(K2')正常运行，新增通过关键节点(红牌楼东站、高笋塘站、营门口北站、成仁站和万年场站)的K4'、K6'和K8'，使途径这些站点需换乘的乘客以无缝换乘方式解决线路优化前需换乘才能到达目的地的出行，这样既能提升乘车舒适度，又能减少上下车排队人数，这就使得二环BRT上乘客的换乘系数由当前1．5下降到优化线路之后的1．25。换乘系数的适当降低势必提升乘车的舒适性、安全性和便捷性，有利于进一步提升公交服务水平和吸引力，进而提高城市公交出行分担率。

4 结论与启示

本文从优化实际公交线路出发，用滤波组合抽象和解释现实问题，突破了基于概率意义下的次优选择的优化方法，能有效改善公交服务现状，使线路与客流走向更趋一致，对提高公交线网的运营效率具有积极意义。在具体的推理、模拟及优化过程中，认为在城市公交的管理实践中，应重视以下几点:

(1)公交线路长度与城市规模、市民平均乘距有关，一般而言，20公里为宜。线路过长，导致道路堵点增加，势必影响行车速度，增加系统运行费用，故需重视和加强公交专用道建设;线路过短又不利于运行调度，还会增加乘客的换乘次数，故不能忽视中小型换乘站的建设，以确保每个规划线网内，任意OD出行方案，仅需换乘一次可达。

(2)BRT享有独立路网，其大运量、便捷性和准点性等优势，常规公交无法比拟，但BRT代价大。就成都BRT而言，单就一条线，道路资源尚未得到充分利用，资源承载力还存有较大挖掘空间，通过线网优化使其真正形成具有柔性的快速公交路网以满足乘客的刚性出行需求，是城市快速公交健康快速发展的必经之路。

(3)通过线网优化，减少乘客换乘次数，并不断完善与常规公交和轨道交通的接驳换乘，实现同台同站无缝换乘，有利于进一步提升公交服务水平和吸引力，提高城市公交出行分担率，优化城市交通的分担结构，实现传统公交向现代公交转型升级。

事实上，本文所提出的基于线网滤波组合逼近的公交线网优化方法，在经验数据基础之上尝试突破既有资源禀赋约束，构造性地创新供给方式以适应潜在市场需要，同样适用于高峰值多峰现象在交通管理、旅游管理、酒店管理等复杂环境的生产运营和组织管理优化问题。通过优化与灵活调整，将复杂系统通过魏尔斯特拉斯定理转化为简单逼近，将多目标问题通过组织划分转换为单目标问题，综合运用数学优化手段减少瓶颈点并辅以管理策略，就能减少不必要的浪费，提高运营效率。

［1］仇保兴．缓解北京交通拥堵:难点与对策［J］．建设科技，2010，(17):14-17．

［2］Zheng S，Kahn M E．Does government investment in local public goods spur gentrification?Evidence from Beijing［J］．Real Estate Economics，2013，41(1):1-28．

［3］李京文，杨正东．中国新型城市化与低碳绿色交通转型之路——在亚欧能源政策网2013年国际会议上的主旨报告［J］．工业技术经济，2014，33(1):3-10．

［4］Madanat S，Horvath A，Mao C．Potential greenhouse gas emission reductions from optimizing urban transit networks［R］．California:Institute of Transportation Studies，University of California，Berkeley，2016．

［5］曾鹦，李军，朱晖．面向换乘行为的城市公交客流分配及应用［J］．系统管理学报，2015，24(1):22-31．

［6］Agostino N，Umberto C，Luca R．A schedule-based assignment model with explicit capacity constraints for congested transit networks［J］．Transportation Research Part C:Emerging Technologies，2012，20(1):16-33．

［7］Yu B，Yang Z Z，Jin P H．Transit route network designmaximizing direct and transfer demand density［J］．Transportation Research Part C:Emerging Technologies，2012，22(5):58-75．

［8］张凯，秦斌斌，刘用渗，等．城市轨道交通线网评价研究［J］．铁道工程学报，2014，(3):97-101．

［9］孙杨，孙小年，孔庆峰，等．轨道交通新线投入运营下常规公交网络优化调整方法研究［J］．铁道学报，2014，(3):1-8．

［10］谢仲磊．基于IC卡数据的公交线网评价［J］．交通标准化，2013，(21):124-126．

［11］房晋源．基于基尼系数的公交线网评价均衡性研究［J］．交通运输系统工程与信息，2012，12(4):178-183．

［12］Cipriani E，Gori S，Petrelli M．Transit network design: a procedure and an application to a large urban area［J］．Transportation Research Part C:Emerging Technologies，2012，20(1):3-14．

［13］胡启洲，张卫华．基于信息熵的公交线网优化方案余弦排序［J］．系统工程理论与实践，2008，(12):121-127．

［14］李彬，杨东援，孙四平．竞争性公共交通客运需求预测模型［J］．预测，2001，20(4):72-74．

［15］胡启洲，邓卫．基于线性分派法对公交线网优化方案排序［J］．系统管理学报，2007，(4):442-446．

［16］李子木，陈学武，纪尚志．基于BRT吸引圈层的公交线网优化重构方法——以常州市为例［J］．武汉理工大学学报(交通科学与工程版)，2013，37(3):491-495．

［17］Cancela H，Mauttone A，Urquhart M E．Mathematical programming formulations for transit network design［J］．Transportation Research Part B:Methodological，2015，77:17-37．

［18］Ngamchai S，Lovell D J．Optimal time transfer in bus transit route network design using a genetic algorithm［J］．Journal of Transportation Engineering，2003，129 (5):510-521．

［19］于滨，杨永志，杨忠振，等．基于直达客流密度最大的公交线网优化［J］．哈尔滨工业大学学报，2009，41 (2):205-207．

［20］陈蛇，张颖，邱法军．传统城市公交向现代服务业转型升级的途径［J］．经济体制改革，2014，(2):126-129．

Research on Efficiency of Public Transport Using Filtering Combination Approximation——Evidence from the Elevated BRT of the Second Ring in Chengdu

CUI Hong-wei1，ZENG Ying2，CHEN She2
(1．College of Economics Mathematics，Southwest University of Finance and Economics，Chengdu 611130，China; 2．Chengdu Academy of Social Sciences，Chengdu 610023，China)

In order to meet the public transportation needs of the rush hour，more buses are being configured，resulting in inefficient operation．Thus，the filtering combination approximation is put forward to improve the efficiency of urban transit by optimizing bus lines．Passenger quantity of each site is obtained through modern information technology，such as IC card，RFID technology，image recognition technology，as well as the transit OD passenger flow survey．The polynomial curve fitting is adopted to fit the real traffic data for traffic function．Multi-peak site is eliminated using filtering．Data mining technology is applied to realize Weierstrass approximation，which is between the site traffic of bus lines of multi-peak with peak value and the original bus lines．Finally，the operability and efficiency are validated using filtering combination approximation to optimize the bus rapid transit network．Meanwhile，the feasible measures of network optimization are put forward．These measures are not only guaranteeing the full coverage of the original line，but also reduce the number of transfer times and the frequency of the buses．

traffic capacity;filtering combination approximation;traffic induction;RFID technology

U491．1

A

1003-5192(2017)04-0069-06

10．11847/fj．36．4．69

2016-10-25

国家社会科学基金资助项目(15XJY008，15XZZ011)