基于渗流井理论的放水试验数值模拟及水文地质参数不确定性分析

孙启明, 柯贤敏, 田国林, 王 玮

(1.长安大学 环境科学与工程学院， 陕西 西安 710054； 2.陕西地矿九〇八水文地质工程地质大队， 陕西 西安 710600)

基于渗流井理论的放水试验数值模拟及水文地质参数不确定性分析

孙启明1, 柯贤敏1, 田国林2, 王 玮1

(1.长安大学 环境科学与工程学院， 陕西 西安 710054； 2.陕西地矿九〇八水文地质工程地质大队， 陕西 西安 710600)

[目的] 建立可靠的地下水数值模型，为煤矿矿坑涌水的预测提供参考。[方法] 采用Modflow-2005中的Conduit Flow Process(CFP)方法对某煤矿放水试验进行模拟，并用局部灵敏度分析方法进行水文地质参数不确定性分析。[结果] 建立了“渗流—管流耦合模型”，经过反复调参，分析拟合结果，求得最佳拟合的水文地质参数。通过灵敏度分析，获得最大的灵敏度参数。[结论] 研究区内含水层渗透性差异比较大，在疏放水过程中要做好预防措施；灵敏度分析结果表明，井管C值对放水试验影响最大，纵向上侏罗系下统延安组渗透系数的影响大于其他含水岩组。

渗流井理论； 渗流—管流耦合模型； Modflow-2005； CFP； 水文地质参数； 局部灵敏度分析

文献参数： 孙启明, 柯贤敏, 田国林, 等.基于渗流井理论的放水试验数值模拟及水文地质参数不确定性分析[J].水土保持通报，2017,37(3)：290-294.DOI:10.13961/j.cnki.stbctb.2017.03.050； Sun Qiming, Ke Xianmin, Tian Guolin, et al. Numerical simulation and analysis of hydrogeological parameter uncertainty based on seepage well theory[J]. Bulletin of Soil and Water Conservation, 2017,37(3)：290-294.DOI:10.13961/j.cnki.stbctb.2017.03.050

放水试验的目的，是以地下水井流理论为基础，通过放水试验过程中水位、水量的变化来反求水文地质参数，评价水文地质条件，进而为预测矿井涌水量和评价地下水资源量等提供依据[1]。数值法目前是求解复杂条件下地下水流和溶质运移问题的主要手段[2]。因此可以采用数值法对放水试验进行模拟研究，但是大多数放水孔并不是常见的竖井，是有一定角度的辐射井，所以对于我们难以用平常的方法来刻画这些“辐射井”。本文以渗流井理论为基础，采用Modflow-2005中的conduit flow process(CFP)方法，对放水试验进行了模拟。CFP是美国地质调查局开发的双重孔隙介质模型，它能够很好地将传统线性层流流态的地下水流运动与离散的管道网络耦合在一起[3-5]。CFP可以模拟层流、紊流状态下的岩溶管道。模型建立后通过有限差分方法来计算不同含水层参数和边界条件下的地下水水位和流量[6]。

目前“渗流—管流耦合模型”已有诸多应用，例如，在北海市混合抽水试验场，通过“渗流—管流耦合模型”，对混合抽水井作用下，不管是混合观测孔的水位还是非混合孔的水位都能很好地拟合[7-9]。郑州市黄河滩地 3 个含水层混合抽水试验求取分层水文地质参数中，利用“渗流—管流耦合模型”建立了此区的模拟模型，求得5层的水文地质参数[10]。渗流井是近年来新兴的一种结构比较复杂的地下水取水建筑物，主要由输水平巷、硐室、渗流孔、集水竖井4个部分组成。渗流井工作时，在“井—含水层”中存在多种流态，含水层中一般为层流，而在“井管”中，通常情况为紊流[11]。渗流井刚开始工作时，出水量主要来自渗流井和其所在含水层，随着工作时间的加长，渗流井及其所在含水层出水量逐渐减少，最终达到稳定。由于放水试验的放水孔的布设结构与渗流井的结构相似，两者不同之处在于放水孔是由煤层向上覆地层打的，由煤层中的巷道排水，无集水竖井，单个硐室，没有平巷连接，也没有河流的渗漏补给，仅依靠含水层的弹性释水补给。因此只需设置合适的边界条件便可利用渗流井的形式模拟放水试验。

本文拟以纳林河2号矿井煤仓的疏放水为研究对象，建立煤仓放水试验的数学模型以及利用MODFLOW建立数值模拟模型。对煤仓疏放水进行模拟，对观测孔的实测降深和放水孔的实测出水量进行拟合，以求得含水层的水文地质参数。

1 实例研究

1.1 工程概况

纳林河2号矿井是基建中的特大型矿井。井田内共含可采煤层5层，其中3—1煤层为主要可采煤层。根据井田勘探资料及前期巷道掘进资料，3—1煤层顶板砂岩裂隙含水层及2煤组顶板砂岩含水层均属于延安组碎屑岩类孔隙裂隙承压水含水层组。目前巷道掘进期间直接充水水源为3—1煤层顶板砂岩裂隙含水层。HB3钻孔位于煤仓附近，根据HB3钻孔揭露地层，纳林河矿井煤仓附近巷道底板位于+580 m水平，距离2—1煤层底板+638 m约为57 m，煤仓设计高度为50 m，仓顶巷道设计高度4.17 m，在煤仓施工的过程中考虑到煤仓施工安全，对煤仓探放水及疏放水工程予以设计。该工程共分为钻探施工、疏放水试验2个阶段。井下疏放水试验分为2个阶段：(1) 单孔放水试验于2012年12月4日至12月11日开展，疏放水量6 188.7 m3； (2) 多孔叠加放水试验于2013年1月4日至1月15日开展，疏放水量13 825 m3。

煤仓探查共设计8个探查钻孔，钻孔设计参数见表1。HB3钻孔揭露地层从上到下分别为：第四系(Q3+4)、白垩系下统洛河组(K1l)、侏罗系中统安定组(J2a)、侏罗系中统直罗组(J2z)、侏罗系下统延安组(J2y)。

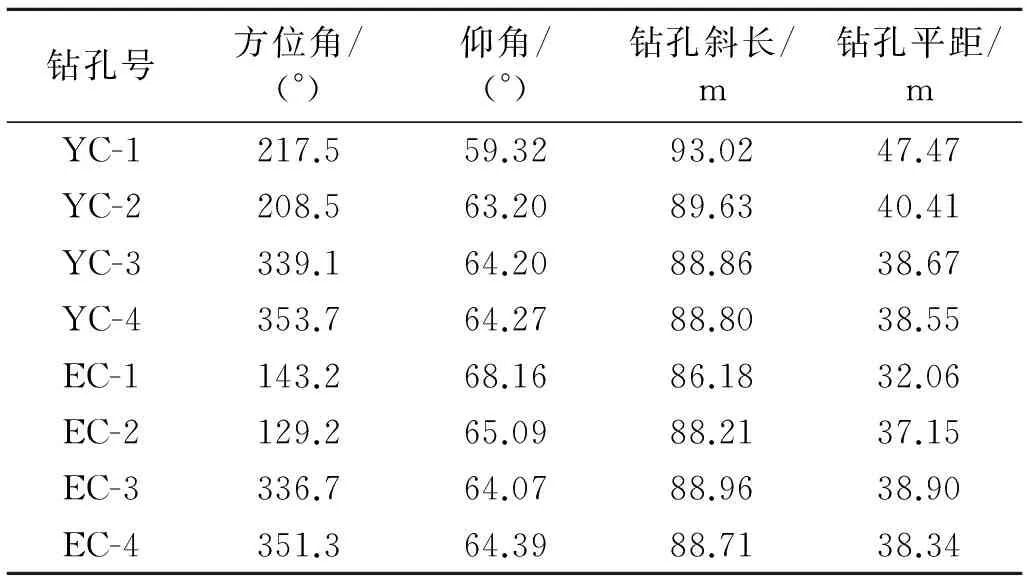
表1 钻孔设计参数一览表

注：钻孔终距80m，终孔层位于2-1煤层上。

1.2 试验过程

本次模拟只选单孔放水试验进行模拟，2012年12月5日11:00开始放水，放水孔为YC-4，压力观测孔为YC-1，YC-2，YC-3，EC-2，EC-3，EC-4，总放水量为1941 m3，中心孔最大降深为163 m。2012年12月7日10:00结束放水，之后进行水位恢复，恢复截止12月8日10:00。YC-4钻孔开始放水至放水结束，放水孔流量变化如图1所示。

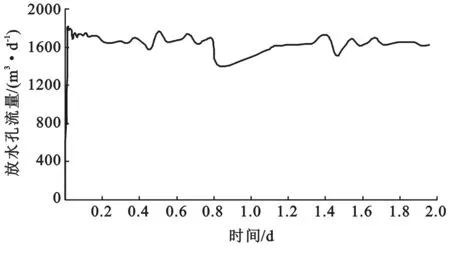
图1 YC-4放水孔流量变化

1.3 水文地质概况

区内含水层主要为第四系萨拉乌苏组孔隙潜水含水层、白垩系下统志丹群(洛河组)孔隙裂隙承压水含水层、安定-直罗碎屑岩类孔隙裂隙承压水含水层及延安组碎屑岩类孔隙裂隙承压水含水层。各含水层均为非均质轴对称各向异性。模拟期间无源汇项。巷道掘进期间对矿井产生威胁的主要含水层是延安组碎屑岩类孔隙裂隙承压水含水层。

2 模型的建立

2.1 水文地质概念模型

模拟区范围：大地坐标X=36 580 446～36 590 446 m，Y=4 209 538～4 219 538 m。

模拟区以布井范围为中心，四周向外延5 km，考虑到放水试验对四周边界影响较小可以忽略，概化为定水头边界。受开采影响的延安组地层碎屑岩类孔隙裂隙承压水含水层埋深较大，与第四系含水层的补给量、排泄量微见明显的水力联系，故将模拟区的顶面设为定水头边界。模拟区底面为侏罗系延安组完整基岩，基岩结构致密，裂隙不发育，构成区域隔水底板。排水口位于煤层所在层，故将这层硐室所在的单元格设为定水头边界，硐室四周不透水，可设为井边界。

2.2 数学模型

采用渗流井方式计算时，井周围地下水三维流特征显著，可将地下水流概化为三维流，水流服从达西定律。为准确刻画井结构，首先采用长方体单元对局部计算域进行加密剖分。

在剖分网的基础上，结合渗流井的结构，以“井管”各段与含水层间的水量交换为纽带，采用“渗流—管流耦合模型”建立数值模型。根据前述水文地质概念模型，模拟区地下水三维非稳定流数学模型为：

式中：Kxx，Kyy，Kzz——x，y，z轴方向的渗透系数(m/d)；H——地下水位标高(m)；Hs——取水建筑物内抽水动水位(m)； ΔH——水头损失(m)；l——2个水头差之间的距离(m)；x,y,z——坐标变量(m)；C——井管过滤器透水性能；Qe——井管与含水层之间的水量交换(m3/d)；Qp——井管内出水量(m3/d)；υ——水动力粘滞系数(m2/s)；g——水重力加速度(m/s2)；d——“井管”的直径(m)；ν——渗流速度(m/s)； Г1——一类边界； Г2——二类边界；N——二类边界外法线方向；D——研究区范围；e——井管管壁的粗糙厚度(m)。

2.3 模型空间和时间离散

利用三维规则网格进行空间上的剖分，本次模拟平面上剖分采用分别平行于x，y轴的100 m×100 m的等间距网格进行剖分，在放水试验范围附近采用5 m×5 m的等间距网格进行加密剖分，在这样的剖分形式下，将整个研究区沿东西向剖分为138列，沿南北向剖分为138行。纵向上根据勘探期间施工的地面钻孔所揭露的地层结构及其分布特征，划分为23层，自上而下包括Q3+41层，白垩系含水岩组分为2层，侏罗系安定组分成2层，侏罗系直罗组分成4层，2—1煤层上侏罗系延安组分成6层，2—1煤1层，2—1煤层下至3—1煤层上侏罗系延安组分为4层，3—1煤层1层，3—1煤层下侏罗系延安组分成2层，每层厚度需要根据实际含水层厚度及井结构进行合理分配。

计算域的剖分不仅包括空间上的剖分，也包括时间上的剖分，本次模拟期选定为2012年12月5日11:00至12月8日10:00，总计1.96 d，根据抽水过程以天为单位对模拟期进行剖分，共划分为58个应力期。

2.4 辐射管刻画

应用CFP的方法刻画辐射管，在CFP输入文件中统计辐射井各节点及管段所处模型中的位置，再赋上相应的节点水头、管段(Conductance)等。

2.5 模型识别

通过分析研究区的水文地质条件，根据不同地段的含水层埋深和补给条件的差异、天然条件下等水位线的形态等水文地质条件差异，以及根据历次水文地质勘查报告、钻孔资料以及抽水试验成果所得结果，同时根据地层的岩性特征和工程经验给定各层参数初始值，经过模型的计算和调试，最终得到各层的水文地质参数。

本次研究把2012年12月5日至2012年12月8日作为模拟期的模型的识别期。首先根据2012年12月5日至2012年12月8日的实测地下水位观测数据进行水文地质参数识别，由钻孔抽水实验求得导水系数、贮水系数等作为数值模拟求参的初始值，通过反复调试、优选水文地质参数，带入模型模拟出计算地下水水位来拟合对应时间段及对应位置的观测孔地下水水位实测资料，部分观测孔的实测降深与计算降深拟合曲线及放水孔计算出水量与实测出水量拟合曲线如图2—5所示。

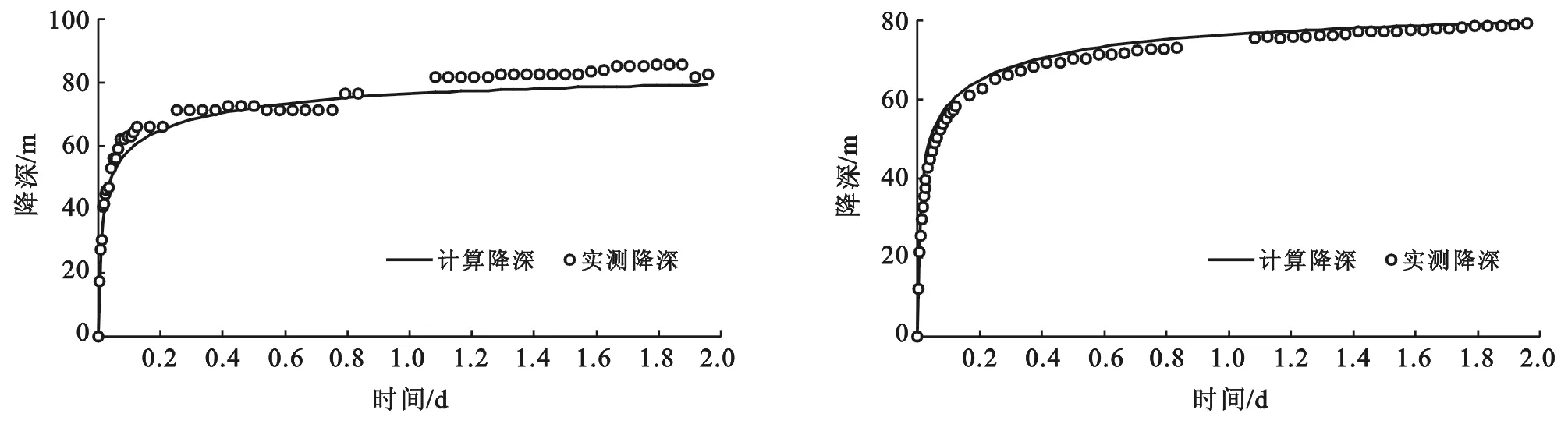
图2 观测孔YC-1计算降深与实测降深拟合 图3 观测孔YC-2计算降深与实测降深拟合

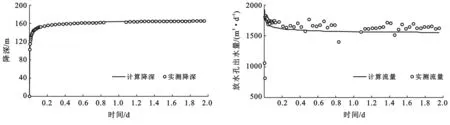
图4 观测孔YC-3计算降深与实测降深拟合 图5 放水孔出水量拟合

通过上述模型地下水水位水量验证分析，水位水量在模拟期的变化趋势基本一致，表明所建模型合理，建立的三维地下水流模型可以用于放水试验模拟计算。

模型识别验证后最终确定出各模型层的参数，各层参数值见表2。将模型识别所得参数与实际抽水实验所得参数对比，所得参数与实际抽水试验所得参数相差不大，表明模型计算结果合理。

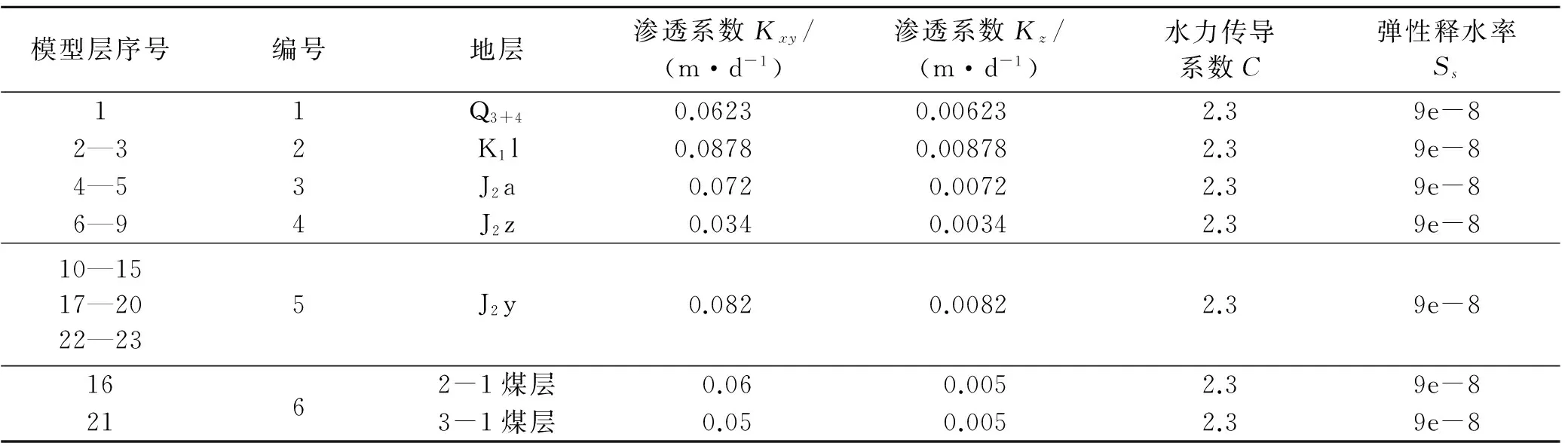
表2 模型各层水文地质参数

2.6 水文地质参数不确定性分析

由于水文地质参数的不确定性导致计算结果的不确定性，影响所建模型的可靠性，因此应用灵敏度分析法对模拟识别后的水文地质参数进行水文地质参数不确定性分析。灵敏度分析方法主要用于定性或定量地评价系统参数的变化对系统结果带来的影响。它包括局部灵敏度分析和全局灵敏度分析[12]。为得到单一水文地质参数对计算结果的影响，本文采用局部灵敏度分析，即改变模型的某一参数而保持其他参数不变，分析模型计算结果对该参数变化的响应。局部灵敏度优点是可操作性强，只针对一个参数，对其他参数取其中心值，即可得到该参数每次发生变化时模型结果的变化量。

以识别验证期末的水位作为基准，以改变参数后的水位变化作为衡量相关参数灵敏度的指标。通过灵敏度分析法可以将不同空间分布、不同种类参数对地下水数值模拟模型的影响程度进行排序，得到对模拟结果影响较大的参数类型及其分布区域[13]。

选取放水孔上端附近的25个代表单元格在识别期末的水位作为基准，分析研究区各区水位对水文地质参数变化的响应情况。灵敏度系数计算公式[13]：

式中：βk——水头H对第k个参数的灵敏度系数； n——研究区内选取的代表单元格； Hi,k′——识别期末各代表单元格的计算水位(m)； Hi,k——灵敏度分析时改变识别参数模拟期末各代表单元计算水位(m)。

分别选取6个分区的水平渗透系数(Kxy)、垂向渗透系数(Kz)、弹性释水系数(Ss)、辐射管过滤器材料的井管水力传导系数C作为不确定性分析的目标参数。计算结果如图6所示。

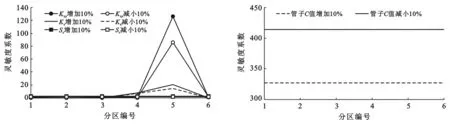
图6 水文地质参数灵敏度计算结果

由图6可以看出： ① 辐射管过滤器材料的井管水力传导系数C对模拟结果影响最大，其次是含水层水平渗透系数Kxy，垂直渗透系数Kz和弹性释水系数Ss对模拟结果的影响相比之下比较微弱。 ② 对于整个含水层各层渗透系数变化对模拟结果的影响来说，侏罗系下统延安组(J2y)裂隙岩类承压含水层组的渗透系数变化对模型影响最大，侏罗系中统直罗组(J2z)裂隙岩类承压含水层组和煤层的渗透系数影响次之，第四系(Q3+4)松散岩类孔隙潜水含水层组、白垩系下统洛河组(K1l)孔隙裂隙岩类潜水含水层组、侏罗系中统安定组(J2a)裂隙岩类承压含水层组的渗透系数对模拟结果的影响微弱。

3 结 论

本文采用渗流井理论对纳林河2号矿井的煤仓放水试验进行模拟，模拟识别期后的实际观测降深和计算降深、实际出水量和计算出水量拟合较好，可以用来指导放水试验。

数值模拟结果表明，区内含水层水平渗透系数和垂直渗透差异较大。其中第四系(Q3+4)松散岩类孔隙潜水含水层组、白垩系下统洛河组(K1l)孔隙裂隙岩类潜水含水层组、侏罗系中统安定组(J2a)裂隙岩类承压含水层组和侏罗系下统延安组(J2y)裂隙岩类承压含水层组的透水性较好，侏罗系中统直罗组(J2z)裂隙岩类承压含水层组一般，煤层透水性较好。根据计算结果，在疏水降压开始初期涌水量较大，应做好预疏放措施，同时还要注意矿井的排水能力应满足要求。

灵敏度分析结果表明，井管的水力传导系数C的灵敏度系数最大，含水层水平渗透系数的灵敏度系数大于垂向渗透系数的灵敏度系数；纵向上，延安组渗透系数的灵敏度系数相比其他含水岩组要大，直罗组和煤层的相对较小。因此，在今后的水文地质勘察工作中，对灵敏度系数大的水文地质参数勘察尽可能提高参数的精度，降低水文地质参数的不稳定性对后续矿坑涌水等工作的预测及评价结果的不利影响。

[1] 房佩贤.专门水文地质学[M].北京:地质出版社,1987.

[2] 薛禹群,吴吉春.地下水数值模拟在我国:回顾与展望[J].水文地质工程地质,1997(4):21-24.

[3] Kuniansky E L, Halford K J, Shoemaker W B. Permeameter data verify new turbulence process for MODFLOW[J]. Ground water, 2008,46(5):768-771.

[4] Shoemaker W B, Birk S, Bauer S, et al. Documentation of a conduit flow process(CFP)for MODFLOW-2005[M]∥Techniques & Methods, 2008.

[5] Reimann T, Hill M E. MODFLOW-CFP: A new conduit flow process for MODFLOW-2005[J]. Ground Water, 2009,47(3):321-325.

[6] 张蓉蓉,束龙仓,闵星,等.管道流对非均质岩溶含水系统水动力过程影响的模拟[J].吉林大学学报:地球科学版,2012(S2):386-392.

[7] 水兵.《地下水不稳定混合抽水的渗流—管流耦合模型及其应用》研究成果简介[J].水文地质工程地质,1994,21(1):49-49.

[8] 陈崇希,林敏,叶善士,等.地下水混合井流的理论及应用[M].武汉:中国地质大学出版社,1998.

[9] Chen Chongxi, Jiao Jiujimmy. Numerical simulation of pumping tests in multilayer wells with non-darcian flow in the well bore[J]. Ground Water, 1999,37(3):465-474.

[10] 陈崇希,胡立堂.渗流—管流耦合模型及其应用综述[J].水文地质工程地质,2008,35(3):70-75.

[11] 王玮.渗流井取水计算模型及其应用[M].西安:陕西科学技术出版社,2010.

[12] 杜京浓,宋汉周,霍吉祥,等.大坝基础渗流数值模拟参数灵敏度探讨[J].低温建筑技术,2014,36(11):90-92.

[13] 吴雯倩,靳孟贵.淮北市地下水流数值模拟及水文地质参数不确定性分析[J].水文地质工程地质,2014,41(3):21-28.

Numerical Simulation and Analysis of Hydrogeological Parameter Uncertainty Based on Seepage Well Theory

SUN Qiming1, KE Xianmin1, TIAN Guolin2, WANG Wei1

(1.CollegeofEnvironmentalScienceandEngineering,Chang’anUniversity,Xi’an,Shaanxi710054,China; 2.Shaanxi908HydrogeologyandEngineeringGeologyTeam,Xi’an,Shaanxi710600,China)

[Objective] To establish a reliable groundwater numerical model, and to provide reference for the prediction of coal mine pit water inflow. [Methods] The flow process conduit(CFP) of Modflow-2005 was used to simulate the dewatering test of a coal mine, and the uncertainty analysis of hydrogeological parameters was carried out using local sensitivity analysis method. [Results] A coupling model of seepage and pipe flow was established. After repeated adjustment and analysis of fitting results, the best fitting of the hydrogeological parameters was obtained. Through sensitivity analysis, the maximum sensitivity parameter was obtained. [Conclusion] There are big differences in the permeability of the aquifers in the study area, precautions should be taken in the process of drainage. The sensitivity analysis results showed that the conductance of the pipe has the greatest influence. Vertically, of Lower Jurassic Yan’an group(J2Y)the permeability was higher than that of other aquifer groups.

theory of horizontal seepage wells; A coupling model of seepage and pipe flow; Modflow-2005; CFP; Hydrogeological parameter; local sensitivity analysis

2016-08-31

2016-10-04

中煤科工集团西安研究院有限公司项目“煤矿斜井涌水量”(220029140533)

孙启明(1992—)，男(汉族)，陕西省安康市人，硕士，研究生，研究方向为水文地质。E-mail：714485096@qq.com。

B

1000-288X(2017)03-0290-05

P641