黄藏寺水库运行方案多方法综合评价浅议
2017-08-01徐士杰黄强
徐士杰,黄强
(西安理工大学水利水电学院,陕西西安710048)
黄藏寺水库运行方案多方法综合评价浅议
徐士杰,黄强
(西安理工大学水利水电学院,陕西西安710048)
多方法评价较单一方法更科学、可靠,可以丰富水资源评价的理论,利用熵值法、模糊物元法、非负矩阵对黄藏寺水库运行方案进行综合评价,三种方法结果的一致性为0.57,评价结果基本一致,利用序号总和理论,得到黄藏寺水库运行最优方案是方案12。多方法评价可以克服单一方法的局限性,较单一方法更可靠。
水资源;综合评价;非负矩阵;黄藏寺
随着水库的建设,运行方式的多样选择已经成为决定水库的效益的直接因素,如何在多种运行方案中确定最有效的方案,已经成为水库运营的一项重要内容。水资源评价的常用方法有主成分分析、层析分析、判别分析、因子分析法、聚类分析法、模糊评价法和灰色评价等[1]。我国学者邓聚龙[2]教授提出了灰色系统概念,并建立灰色系统理论,灰色关联分析法便是该理论应用的主要方面之一。单一方法评价中,方法的选择是个难题,现在也没有确切的理论表示到底哪种方法更优,多方法克服了这一缺点,消弱了人主观选择及一些不确定因素的影响,对最优方案的确定有重要意义。
1 研究区域概况
黑河是我国第二大内陆河,发源地在祁连山中段,河流东起山丹县境内的大黄山,与石羊河流域接壤,西以嘉峪关境内的黑山为界,与疏勒河流域毗邻,北至中蒙边界。大小河流35条,其中集水面积大于100 km2的河流有18条,以黑河为干流。黄藏寺水利枢纽工程位于黑河流域东部子水系。东部子水系包括黑河干流、梨园河及20多条沿山支流,除梨园河在正义峡以上汇入黑河干流外,其它支流出山后即被引灌或渗失于山前冲积扇,无地表水注入黑河干流,黑河干流全长928 km。
2 数据资料
根据黄藏寺水库建设要求,黄藏寺既要解决中游的灌溉的需求,还要满足下游的生态需求,缓解中下游间用水矛盾,提高中下游的保证率。黄藏寺水库对中游灌区的供水范围为以黑河干流为水源的灌区,涉及甘肃省张液市的甘州区、临泽县和高台县等三县(区)的12个灌区。设计年(2020年),黄藏寺水库供水范围内黑河中游灌区需水总需水量10.89亿m3。设计年(2020年))生态总需水量为7.46亿m3。本研究从中下游分水方案的不同:九七分水方案和优化方案,中游灌溉面积的变化情况:耕地维持现状,耕地恢复到2000年的水平,节水水平:低强度节水,中等强度节水,高强度节水这几种情况,把黄藏寺的水库运行方案分为十二种。根据实际情况和黄藏寺水库运行的要求,本文建立四个指标分别是:中游缺水量,下游缺水量,中游灌溉保证率,下游灌溉保证率。其中中游灌溉缺水量与下游生态缺水量是越小越好优型指标,其余指标为越大越好性指标,为消除各评价指标量纲的不同,越小越有优型指标按式(1)对指标进行归一化处理,越大越优型指标按式(2)进行归一化处理。
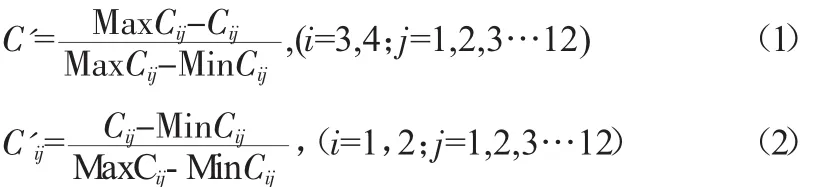
式中:Cij表示第j个方案第i个指标的原始数据,C'ij表示Cij的归一化数据,MaxCij,MinCij表示各方案第i指标的最大值和最小值的原始值。对各个指标的归一化结果见表1。

表1 黄藏寺水库运行各方案的评价指标及归一化处理结果
3 评价方法
3.1 熵值法
熵值法法是一种客观赋权的方法,通过计算指标的的信息熵,根据指标的相对变化程度对系统整体的影响来决定指标的权重,以减少主观因素的影响。熵值法计算过程如下:
3.1.1 归一化的基础上计算指标比重
计算第j项指标下第i年份指标的比重,如式(3)所示,并由此建立数据的比重矩阵Y,如式(4)所示。

式中:m表示方案个数,n表示指标的个数。
3.1.2 信息熵值
计算第j指标下第i年份指标的信息熵值lj,如式(5)所示。其中,K、fij的计算如式(6)和式(7)符号意义如上。

3.1.3 信息效用值
信息效用值为指标的信息熵值lj与1之间的差值,信息效用值结果直接影响权重的大小。信息效用值越大,对评价的重要性越大,权重相应越大,对评价结果的贡献就越大,如式(8)。

3.1.4 权重
利用指标的信息效用值计算指标权重,第j项指标的权重如式(9)。

3.1.5 样本评价
采用加权求和计算综合评价结果,如式(10),其中U为综合评价值,值越大样本效果越好,最后比较所有的U值,排序对各个方案进行评价,确定最优方案。

3.2 模糊物元法
模糊物元分析就是把模糊数学和物元分析有机地结合在一起,对事物特征相应的量值所具有的模糊性和事物众多因素间的不相容性加以分析,综合,从而获得解决模糊不相容问题的一种新方法。其评价步骤如下:
3.2.1 模糊复合物元
模糊物元一有序三元组“事物”、“特征”、“模糊量值”作为描述事物的基本元,如式(11)。

式中:R为模糊物元,M为事物,C为事物所具有的特征,μ μX μ为与C相对应的模糊量值,即特质C对应量值x的隶属度。对于流域水资源配置评价而言,事物M就是指不同的评价方案,特征C指各项评价指标,量值x就是各项评价指标的量化值。用同上的归一化处理得到得到μji形式如式(12)的模糊物元矩阵。

3.2.2 标准模糊物元与差平方复合模糊物元

以Δji表示标准模糊物元与复合模糊物元各项 差的平方,则组成差平法复合模糊物元记为式(14)。

3.2.3 欧式贴近度
水资源优化配置的指标的相对独立性较高,本文采用欧式贴近度来表征各评价方案与标准方案间的贴近程度。如式(15)表示。

式中:ρHj为第j个方案相对于标准事物的欧式贴近度,ωi为个各指标的权重,在本文中采用熵值法确定。其值越大,表示两者越接近;反之,则相差越大。显然,ρHj最大值对应的方案即为评价方法的到的最优方案。
3.3 非负矩阵
非负矩阵的分解原理(NMF)是由Lee和Seung1999年在《Nature》上提出来的。他是通过将多维数据转换为低维数据来辨析数据潜在的结构特征,可以为获得水资源多方案评价中的特征信息提供依据。
3.3.1 建立方案指标矩阵
设水资源配置中有n个可行方案和m个评价指标,Zij为第j个方案的第i个指标,建立的如下的方案矩阵(16)
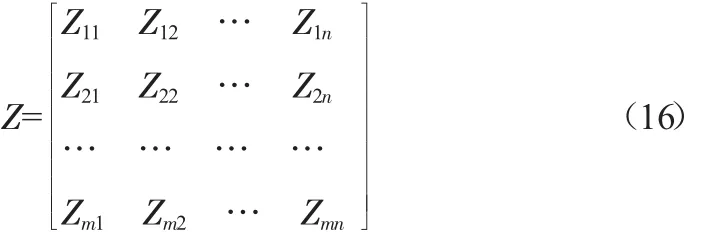
根据非负矩阵的分解原理,将矩阵Z近似分解为列向量V和行向量H。
3.3.2 近似分解矩阵
近似分解偏差平方和的定义如下式(17):

为最大近似的分解矩阵Z,偏差平方和f达到最小化。因此对和求偏导并令个偏导数为0得式(18)(19):

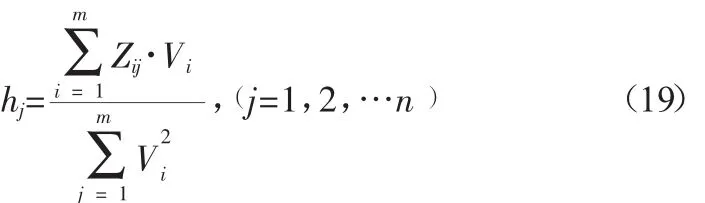
3.3.3 加‘1’限制唯一化
当f最小化时,由于V与H呈现倍数关系,V和H有无数种组合,为使Z得分解的唯一性,增加独立条件如式(20):

在约束条件下,可以得到相应的偏度如式(21):
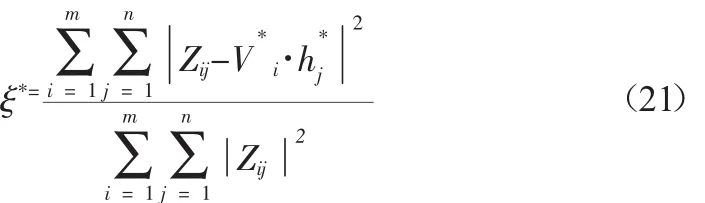
列向量V*和H*行向量在方案优选中分别被称为基向量和权向量,其意义在于:以基向量V*为公度向量,通过权向量H*中值来衡量Z中列向量的大小。权向量中某元素的值越大,对应的方案越优,据此就可以对所有方案进行优劣排序。最后用改进的布谷鸟算法对方程求解。
3.4 多方法的结果分析
运用MTLAB计算。对多方案进行评价时,运用不同原理的的评价方法,可能存在评价结果的一致。因此,运用多方法评价后,还要对评价结果的一致性进行分析。
3.4.1 结果的一致性分析。
利用N种评价方法对M个方案进行排序,先判断任意两种方法结果的一致性,计算公式(22)(23)如下:

式中:CD(k,l)为第k种与第i种方法评价结果的一致程度,其中1≤k,l≤N;uf(m)为两种方法对第m(1≤m≤M)个方案排序的一致性判断指标;i、j分别是第k种和第l种评价方法对第m个方案的排序位置。当,k=l时,CD(k,l)1.0。
多方法评价结果的整体一致性指标OC的计算公式(24)为:

当OC=0时评价结果完全矛盾;当0<OC≤0.5时,评价结果矛盾显著;当0.5<OC<1时,评价结果基本一致;当OC=1时,评价结果完全一致。
3.4.2 序号总和理论通常情况,多方法评价结果的整体一致性指标大于0.5。这里重点介绍当结果基本一致时如何进行最后的优选评定,序号总和理论就是解决这一问题的有效方法。其基本思路就是各评价方案在多方法中的排序结果进行总和,按序号总和的大小对各方案进行最终排序。
4 结果分析
4.1 熵值法结果
熵值法确定的各指标的权重如表2和熵值法各方案的排序结果如表3。

表2 指标权重

表3 熵值法的各方案的的排序
4.2 模糊物元法结果
利用模糊物元法确定的排序结果如表4。

表4 模糊物元法各方案的排序
4.3 非负矩阵评价结果
利用非负矩阵排序的结果如表5。
4.4 一致性分析与序号总和理论优选
通过式(24)计算,熵值法,模糊物元,非负矩阵综合评价的一致性为0.57,评价结果基本一致,符合一致性原则。通过序号总和理论得到各方案的序号和表6。

表5 非负矩阵的各方案的排序

表6 序号总和结果
通过序号总和理论得到方案12最优,即实行优化方案,耕地面积减少到2000年的水平,同时进行高节水方案。方案1效果最差。
5 结论
黄藏寺水库运行方案(近期水平年2020)多样,存在选择困难。本研究运用多种方法进行综合评价,并运用序号总和理论进行方案优选得道如下结论:
(1)通过熵值法,模糊物元,非负矩阵法评价,得到在黄藏寺水库运行方案中第12种方案最好,方案1的评价结果最差。
(2)不同评价方法由于基本原理有所差异,即便在同一指标体系下采用相同的指标权重,也可能会出现不一致的评价结果。因此,当多种方法评价的结果基本一致时,采用序号总和理论可以解决单一评价方法的局限性,评价结果更为可靠。
[1]付强.水资源系统分析[M].北京:中国水利水电出版社,2012: 178-181.
[2]邓聚龙.灰色控制系统[J].华中工学院学报,1982,10(3):9-18.
Preliminary Discussion on Multi-method Comprehensive Evaluation of Huangzangsi Reservoir Operation
Xu Shijie,Huang Qiang
(Institute ofWater Conservancyand Hydroelectric Power,Xi’an science and technologyuniversity,Xi’an 710048,Shaanxi)
Multi-method evaluation is more scientific and reliable than the single method,and the theory of water resources evaluation can be enriched.Entropy method,fuzzy matter-element method and non-negative matrix are used to evaluate Huangzang reservoir operation plan,and the consistency of the three methods is 0.57,the evaluation results are basically the same,using the serial number theory,the optimal scheme for the reservoir operation of Huangzang Si is program 12.Multi-method evaluation can overcome the limitations ofa single method,it is more reliable.
Water resources;comprehensive evaluate;non-negative matrixand HuangzangSi
TV697.13
B
1673-9000(2017)03-0022-03
2017-02-16
国家自然科学基金项目(91325201)。
徐士杰(1991-),男,江西高安人,在读硕士研究生,主攻方向:水资源系统工程。
黄强(1958-),男,陕西西安人,教授,博士生导师,主要从事水资源系统工程研究。
