富水填土区基坑开挖引起的地表沉降研究

靳晓光，侯晓鹤，孙志岗，张浩凌

(1.重庆大学 土木工程学院，重庆 400030；2.山地城镇建设与新技术教育部重点实验室，重庆 400030)



富水填土区基坑开挖引起的地表沉降研究

靳晓光1,2，侯晓鹤1,2，孙志岗1,2，张浩凌1,2

(1.重庆大学 土木工程学院，重庆 400030；2.山地城镇建设与新技术教育部重点实验室，重庆 400030)

探讨了地下水渗流作用下填土区基坑开挖引起的周围地表沉降估算方法，推导了基坑开挖引起的地表沉降计算公式；结合富水填土区轨道交通区间深基坑开挖工程实例，对基坑周围地表沉降进行了理论分析和数值模拟研究。结果表明：地下水渗流是引起基坑周围地表沉降的重要原因之一。该方法实用性及可靠性较好，是类似地质环境条件下一种较好的地面沉降估算方法。

铁道工程；富水填土区；基坑开挖；渗流；数值模拟；地表沉降

0 引 言

随着城市的建设与发展，城市中的深基坑工程越来越多，深基坑的工程事故也时有发生。事故常由地下水渗流作用所引起，因此深基坑工程中的地下水问题越来越受到工程师们的重视。目前，在深基坑工程设计中若遇到地下水问题，一般都是采用静水压力计算，很少考虑地下水渗流对深基坑工程的影响，计算结果与实际工程并不相符。如何较好地处理地下水渗流问题是基坑工程中一个重要的研究课题。

关于基坑周围地表沉降计算，R.B.PECK[1]通过工程实测统计得出了一套与土性及开挖深度有关的地表沉降估算方法；简艳春[2]采用有限元法分析了一系列软土基坑工程典型实例，根据计算结果和实测值提出了软土基坑墙后地表沉降的概率分布曲线，按照地层损失法思路，推导了由支护墙侧向变形值求解墙后地表沉降的适用公式；英国学者J.N.SHIRLAW[3]针对不同含水量地层采用不同开挖方法所引起的地表沉降问题，通过大量实测资料，提出了地层损失和沉降的预测公式，并提出了由于土的流变性而造成的沉降长期性的问题；LEE In-Mo等[4]通过对韩国过江隧道的理论分析和数值计算研究，得出隧道在承受水压力时的受力状态、盾构开挖面承受渗流压力的规律、以及隧道周围渗流场的分布变化情况；T.I.ADDENBROOKE等[5]、C.K.SHEN等[6]研究了盾构隧道施工后地层中地下水运动的长期特性；平扬等[7]将比奥固结理论扩展应用于弹塑性分析领域，将渗流场水力作用与应力场耦合，通过有限单元法模拟，得到了深基坑开挖及降水过程中，开挖范围及邻近区域地面沉降等环境效应的基本规律，为深基坑开挖设计与信息化施工提供了借鉴。L.ZEEVAERT[8]认为基坑周围地表沉降的主要影响因素有2项，即由于地下水位变化引起的地表沉降和支护结构的侧移引起的地表沉降。

笔者以重庆轨道交通环线工程华龙站—重庆西站区间为依托，运用大型有限元软件Midas/GTS，采用理论分析与数值模拟相结合的方式，研究了深基坑开挖对周边地表沉降影响规律，推导出基坑开挖引起的地表沉降计算公式，为富水区明挖区间深基坑等类似工程提供优化设计方法。

1 工程概况

1.1 工程简介

重庆轨道交通环线工程华龙站—重庆西站区间处于现有道路位置，原始地形为一沟谷，不断汇集地下水，周边建构筑物多。地勘资料显示，在区间YDK 50 + 200.000～YDK 50 + 390.922段主要为砂质泥岩和砂岩互层，上覆回填土层较厚，土层厚度8.10～16.50 m，基坑开挖深为20～23 m，地下水位高(图1)，基坑开挖时出水量大。

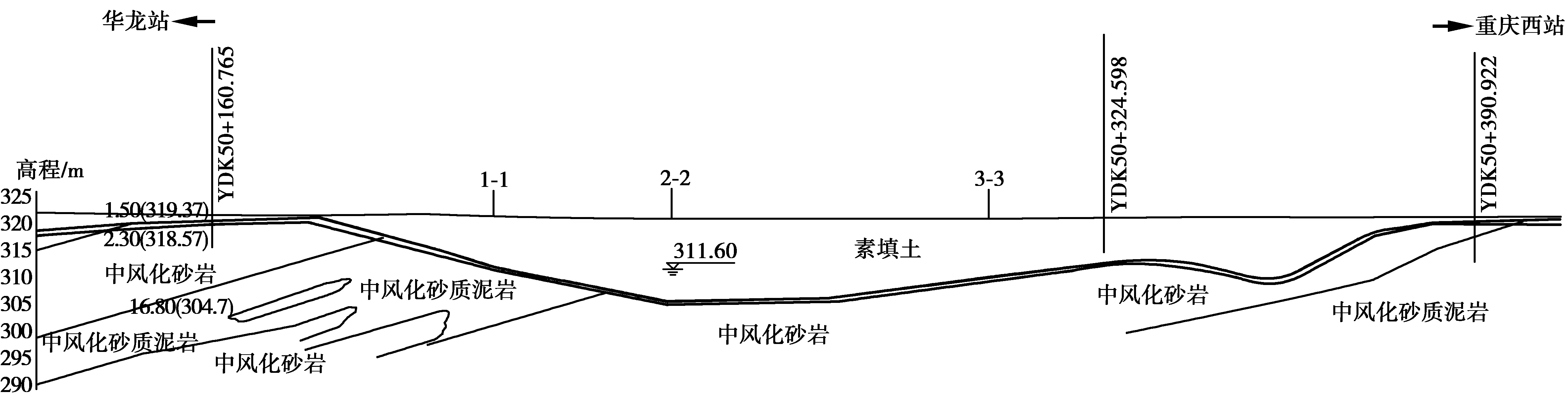
图1 轨道区间明挖段纵断面Fig. 1 Profile diagram of open excavation section at rail transit interval

1.2 基坑土层物理力学参数

重庆轨道交通环线工程华龙站—重庆西站区间地勘资料岩土体物理力学参数，如表1。

表1 基坑土层物理力学参数

2 地表沉降理论分析

2.1 墙后地表沉降形态

根据工程实践经验，地表沉降的2种典型曲线为三角形沉降曲线和凹槽形沉降曲线。三角形沉降曲线主要发生在地层较软弱且墙体入土深度又不大时，墙底处有较大的水平位移，墙体旁边则出现较大地表沉降；凹槽形沉降曲线主要发生在有较大的入土深度或墙底入土在刚性较大的地层内，墙体的变位类同于梁的变位，此时地表沉降的最大值不是在墙边，而是位于距墙一定距离的位置处。笔者主要研究凹槽形沉降曲线。

凹槽形沉降曲线地表沉降范围为[9]

(1)

凹槽形地表沉降曲线为

(2)

式中：δmax为最大沉降值，mm；xm为最大地表沉降值所处的位置(距墙顶的距离)，mm，如图2；r为沉降盆地计算影响半径，mm，可近似为地表沉降影响范围与最大地表沉降值距墙顶的距离的差值，即r≈x0-xm。

图2 基坑开挖引起支护结构侧移和地表沉降Fig. 2 Sideway of supporting structure and ground surface settlement incurred by foundation pit excavation

标准正态分布曲线与凹槽形地表沉降曲线相似。因此可将凹槽形地表沉降曲线看作修正后的正态分布曲线。

2.2 计算方法

2.2.1 支护结构变位曲线包络面积计算方法

支护结构变位数值可以通过实测得到，用顶点式方程可以拟合出支护结构的侧向位移曲线。当桩有较大的入土深度或桩底入土在刚性较大的地层内，桩身的变位类同于梁的变位，即桩身变形为抛物线形。设抛物线顶点式为

f(z)=a(z-zm)2+ym

(3)

式中：zm、ym为支护结构极值点坐标。

将极值点坐标代入式(3)即可求得系数a值。

排桩插入中风化岩石中，插入点处侧向变形可近似为0，若知支护结构极值点(zm，ym)，可算得

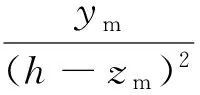
(4)

支护结构侧向位移曲线围成的面积为

(5)

2.2.2 地表沉降曲线包络面积计算方法

(6)

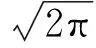
(7)

将式(7)代入式(6)，得

(8)

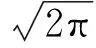
(9)

查表可知：

Φ(2.51)≈0.993 8≈1

(10)

将式(7)～ 式(10)代入式(5)得

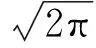
(11)

2.2.3 地表沉降计算方法

利用支护结构的侧向位移面积与地表沉降面积相等的原则，则

Sw=Sa

(12)

将式(5)、式(11)代入式(12)，得

(13)

2.3 基坑开挖引起的地表沉降计算

笔者选取基坑的3个断面进行计算，断面编号分别为1-1断面、2-2断面、3-3断面，里程分别为YDK50+211.8、YDK50+244.2、YDK50+302.1，钻孔编号分别为HHX7、BK1、HHX13。

该深基坑围护结构主要采用排桩 + 钢支撑支护，排桩为钻孔灌注桩，插入中风化岩深度3m，墙后地表沉降形态符合凹槽形沉降曲线。结合现场监测数据，运用沉降曲线计算公式(11)，得出基坑开挖引起的地表沉降值。

表2 基坑桩顶变形位移和支护结构变形最大位移Table 2 Transformation displacement of pile block in foundation pit and the maximum transformation displacement of supporting structure

将表2中数据代入式(4)、式(5)、式(13)得到的结果如表3。

从表2、表3可以看出：①抛物线系数a为负值，支护结构侧移能取得最大值；②桩顶水平位移较小，桩的最大水平位移发生在离地表一定距离位置处；③地表最大沉降不是在支护结构旁，而是位于离支护结构一定距离的位置处。

表3 基坑开挖引起的地表沉降值

将表2、表3的数据代入式(2)，即可得到各断面的地表沉降曲线：

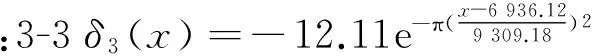
由地表沉降曲线可以得出这3个断面任意一点地表沉降值。

3 数值模拟分析

3.1 地下水渗流引起的地表沉降

基坑上部地层为厚薄不一的回填土层，回填土最大厚度为16.50 m，左侧部分地层为中风化砂质泥岩，下部地层为中风化砂岩。基坑两侧土层分布并不相同。现以基坑左侧土体为研究对象，将基坑左侧土体在地下水渗流作用下的地表沉降与上述理论计算的地表沉降进行对比分析，得出地下水渗流作用引起的地表沉降在总的地表沉降中所占的比重。

3.1.1 数值计算模型

笔者使用Midas/GTS有限元计算软件建立三维计算模型，对地下水渗流过程中地表沉降变形进行数值模拟。模拟中假定工程条件及仿真方法如下：

1)地铁区间场地地势平坦，土体为理想各向同性弹塑性材料，采用Mohr-Coulomb本构模型。

2)不考虑土体固结引起的长期沉降。

3)假定各层土中的物理力学参数保持不变。

有限元计算模型如图3，沿轨道环线纵向长126 m，里程从YDK 50+199.5到YDK 50+325.5。横向延伸长度为50 m，高度为29 m，模型总共14 980个单元，16 956个节点。将土体单元类型设置为3D实体单元。

图3 计算模型和网格划分Fig. 3 Calculation model and mapped meshing

3.1.2 边界条件

模型的边界条件：表面自由，两个长面施加x向约束，两个短面施加y方向的约束，底面施加x和z方向的约束。

3.1.3 数值模拟结果与分析

通过MIDAS/GTS数值模拟软件计算地下水渗流引起的基坑周围地表沉降，然后与所计算的基坑开挖引起基坑周围地表沉降相对比，得出地下水渗流作用引起的地表沉降在基坑开挖引起的地表沉降中所占的比重。计算结果如图4。

图4 地下水渗流引起的地表沉降云图Fig. 4 Cloud picture of ground surface settlement incurred by underground water seepage

根据所计算的基坑开挖引起的最大地表沉降距离基坑边缘的距离，以及1-1断面、2-2断面、3-3断面的里程，可以确定基坑开挖引起的最大地表沉降的位置(坐标)，从数值模拟结果中提取出此位置的渗流引起的地表沉降值，如表4。

由表4可以看出：理论计算的地表沉降的大致范围为12.11～15.32 mm，而地下水渗流作用所引起的地表沉降大致范围为3.88～4.61 mm。地下水渗流作用占总的地表沉降量的1/3左右，这一部分的地表沉降十分可观，在估算基坑开挖引起地表沉降时，地下水渗流作用不能被忽略，否则可能会造成极大的工程事故。

表4 基坑地表沉降值

3.2 基坑开挖引起的地表沉降

3.2.1 数值计算模型

采用MIDAS/GTS数值模拟软件计算基坑引起的基坑周围地表沉降，有限元计算模型和网格划分与上节相同，如图3。将土体单元类型设置为3D实体单元。

围护结构主要采用排桩 + 钢支撑支护，排桩为直径1 m，间距1.8～2.1 m的钻孔灌注桩，钢支撑为直径609 mm，壁厚16 mm的钢管支撑。为模拟支护结构的工作性状，将钻孔灌注桩、钢支撑、钢围檩设置为梁单元，计算模型采用弹性本构模型。

在模拟过程中，考虑了地下水渗流作用的影响。在流固耦合分析时，土体变形及受力情况受到了地下水渗流影响，故在 Midas/GTS 中地下水对基坑的压力需手动加载。

整个基坑开挖过程分8步进行：第1步，初始渗流稳态分析，得到初始孔压分布；第2步，初始位移分析，得到初始地应力场，并将自重作用下的位移清零；第3步，桩的施工，建立土体与桩之间的接触关系；第4～8步，基坑开挖、支撑架设与地下水位降低的过程。

基坑土层物理力学参数见表1，支护结构参数见表5。

表5 支护结构参数

3.2.2 边界条件

模型的边界条件：表面自由，两个长面施加x向约束，两个短面施加y方向的约束，底面施加x和z方向的约束。

3.2.3 数值模拟结果与分析

图5为有限元模拟结果，图6为基坑开挖完成后各断面数值模拟结果、理论计算结果与监测结果地表沉降曲线对比。

图5 基坑开挖完成后竖直方向位移云图Fig. 5 Cloud picture of displacement on the vertical direction after completion of foundation pit

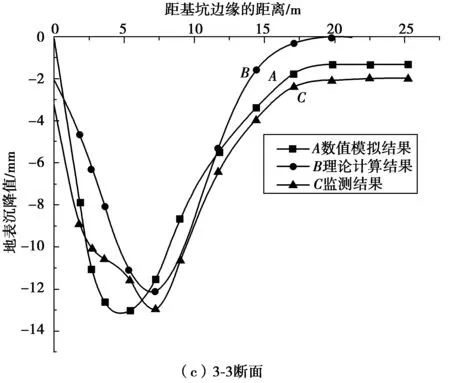
图6 3个断面地表沉降Fig. 6 Ground surface settlement of three cross-sections

由图5、图6可以看出，地表沉降最大沉降值为14.28 mm，发生在离基坑一定距离位置，而在基坑边缘处因为有钢支撑存在，使得地表沉降值较小，符合凹槽性沉降曲线的规律。

由图6可以看出，这3个断面的数值模拟地表沉降曲线均与理论计算所采用的修正后标准正态分布曲线近似。相同之处是它们的变化趋势相同，地表沉降曲线随着距基坑边缘距离的增加先增大后减小，最后趋近于一常数；不同之处在于，理论计算的地表沉降曲线随着距离基坑边缘距离的增加，其值逐渐趋近于0。而数值模拟在整个模型中都考虑了地下水渗流作用，所以其沉降曲线随着距离基坑边缘距离的增加，其值并没有趋近于零，而是逐渐趋近于某一数值。由于距离基坑边缘较远，地下水渗流作用影响并不大，只有1 mm左右。监测结果曲线与理论计算曲线和数值模拟曲线在靠近基坑位置处略微有些差别，这是因为在基坑边缘附近有行车道，会给地面施加一定的活荷载。但变形趋势与最大地表沉降值以及其发生的位置结果和理论计算结果、数值模拟结果差别不大，可以进行对比分析。

1-1断面、2-2断面、3-3断面数值模拟地表沉降最大值分别为14.06、15.14、13.01 mm，地表沉降最大值发生的位置都在理论计算地表沉降最大值附近。这是由于数值模拟考虑了地下水的作用，使得地表沉降最大值存在一定偏差，再者是因为网格具有一定的长度，使得数值模拟结果并不能精确到任何一点，但理论计算地表沉降最大值位置处的数值模拟值与其最大值相差不大，可以进行对比分析。

由图6可以看出，数值模拟与监测的地表沉降的范围比理论计算大，这表明了理论计算得出的地表沉降影响半径结果较小。原因有2个：①因为地下水渗流作用的影响；②由于地层变化的不均匀性，在理论计算中，并没有考虑到地层变化的不均匀性。现将理论计算沉降值与同一位置处数值模拟和监测地表沉降值进行对比，见表6。

表6 数值模拟沉降值和理论计算沉降值对比Table 6 Contrast chart of ground settlement values calculated from numerical simulation and theoretical calculation

由表6可知，理论计算地表沉降结果与数值模拟和监测的地表沉降结果虽然有所差别，但相差不大，最大的误差率也只有9.7%，能够满足工程实际的要求。因此，在遇到类似地质环境条件工程问题时，用文中推荐的地表沉降计算公式进行地表沉降计算，可以快速便捷的计算出地表沉降值，且可靠性较高。

4 结 论

1)地表沉降曲线可用修正后的标准正态分布曲线来表示，数值模拟结果和监测结果也验证了地表沉降符合修正后的标准正态分布曲线这一规律。

2)在估算基坑开挖引起的地表沉降时，地下水渗流作用引起的地表沉降占总地表沉降的1/3左右。这部分地表沉降所占比例较大，在进行基坑设计和施工时不能被忽略。

3)从理论计算地表沉降曲线与数值模拟和监测的地表沉降曲线的对比分析看，无论是地表沉降影响范围还是最大地表沉降值都相差不大，能够满足工程实际的要求。该方法实用性及可靠性较好，是一种较实用的地面沉降估算方法。

[1] PECK R B. Deep excavations and tunneling in soft ground [C]// Mexico City:Proceedingsof7thInternationalConferenceonSoilMechanicsandFoundationEngineering, 1969: 225-290. http://wenku.baidu.com/ link?url=MQzSHt3AJN_qHK2ZjeEdTuP06 kKW54KyTQDBffGCJLhHcZG6Nc_DiPn-1a93em94Z9fkyZhtC8nHb awKV05_zbUQdDrdD1RYtJeEExVVqV_.

[2] 简艳春.软土基坑变形估算及其影响因素研究[D].南京:河海大学, 2001:16-27. JIAN Yanchun.Computation&StudyontheDeflectionoftheBracedStructureandItsAffectionFactorsinExcavationofSoftSoil[D]. Nanjing: HoHai University, 2001:16-27.

[3] SHIRLAW J N. Subsidence owing to tunneling .II. Evaluation of a prediction technique: Discussion [J/OL].CanadianGeotechnicalJournal,1994,31(3):463-466.http://www.nrcresearchpress.com/doi/abs/10.1139/t94-054.

[4] LEE In-Mo, NAM Seok-Woo. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels [J/OL].TunnelingandUndergroundSpaceTechnology, 2001, 16(1): 31-40.http://wenku.baidu. com/link?url=UJj7DBPDmj0n5TU gpn6Fd6t4gxLAJNOI5lzZQybV94_urzDEuwRhfYwahPy3AmfG8jm2 tpgcl5asYCqOHZ2QQ0mrqSqgb2U4mQpu96uIn8O.

[5] ADDENBROOKE T I, POTTE D M, SHIN J H. A numerical study the effect of groundwater movement on long-term tunnel behavior [J/OL].Géotechnique,2002,52(6):391-404. https://www.researchgate.net/ publication/239410932_A_numerical_study_of_the_effect_groundwater_movement_on_ling-term_tunnel_behaviour.

[6] SHEN C K, BANG S, HERRMANN L R. Ground movement analysis of earth support systems[J/OL].JournaloftheGeotechnicalEngineeringDivision, ASCE, 1981, 107(12): 1609-1623.https://www.researchgate.net/publication/279888128_Ground_movement_analysis_of_earth_support_systems.

[7] 平扬,白世伟,徐燕萍.深基坑工程渗流-应力耦合分析数值模拟研究[J].岩土力学,2001,22(1):37-41. PING Yang, BAI Shiwei, XU Yanping. Numerical simulation of seepage and stress coupling analysis in deep foundation pit [J].RockandSoilMechanics, 2001, 22(1): 37-41.

[8] ZEEVAERT L.难处理地基的基础工程[M].陆焕生译.北京:中国水利水电出版社,1982:85-87. ZEEVAERT L.FoundationEngineeringforDifficultSubsoilConditions[M]. LU Huansheng, translation. Beijing: China Water & Power Press, 1982:85-87.

[9] 刘建航,侯学渊.基坑工程手册[M]. 北京:中国建筑工业出版社,1997:213-216. LIU Jianhang, HOU Xueyuan.FoundationPitEngineeringHandbook[M]. Beijing: China Architecture & Building Press, 1997: 213-216.

(责任编辑：田文玉)

Ground Surface Settlement Incurred by Excavation of Foundation Pit in Watery Filling Area

JIN Xiaoguang1, 2, HOU Xiaohe1, 2, SUN Zhigang1, 2, ZHANG Haoling1, 2

(1. School of Civil Engineering, Chongqing University, Chongqing 400030, P. R. China; 2. Key Laboratory of New Technology for Construction of Cities in Mountain Area of the Ministry of Education, Chongqing 400030, P. R. China)

The estimation methods of the ground surface settlement incurred by the foundation pit excavation of filling area influenced by underground water seepage were discussed. The computation formula of the ground surface settlement caused by the foundation pit excavation was also deduced. Combining with the excavation project case of deep foundation pit at rail transit interval in watery backfilling area, both theoretical analysis and simulation study of the ground surface settlement around the foundation pit were carried out. The results show that underground water seepage is one of the important reasons for the ground surface settlement around the foundation pit. With good practicability and reliability, the proposed method is useful in estimating the ground surface settlement in similar geological environment.

railway engineering; watery filling area; foundation pit excavation; seepage; numerical simulation; ground settlement

10.3969/j.issn.1674-0696.2017.07.09

2016-11-04；

2017-03-14

重庆市国土资源和房屋管理局科技计划项目(KJ-2015028)

靳晓光(1967—)，男，山东宁津人，教授，博士后，主要从事岩土工程、隧道与地下空间工程、道路工程、地质工程等方面的研究。E-mail：Jxgcqu@163.com。

侯晓鹤(1992—)，男，河南许昌人，硕士研究生，主要从事岩土工程方面的研究。E-mail：457656743@qq.com。

U216.4；TU46.3

A

1674-0696(2017)07-051-07