基于变均布霍尔系数的磁控热防护系统霍尔效应影响∗

李开 柳军 刘伟强

(国防科学技术大学航天科学与工程学院,长沙 410073)

基于变均布霍尔系数的磁控热防护系统霍尔效应影响∗

李开 柳军†刘伟强

(国防科学技术大学航天科学与工程学院,长沙 410073)

(2016年9月18日收到;2016年12月6日收到修改稿)

为研究霍尔效应对磁控热防护系统的影响机理,建立并验证了热化学非平衡流场、外加磁场、感应电场的多场耦合数值求解方法.基于均布霍尔系数模型分析了霍尔效应在两种不同磁场强度B0、不同壁面导电条件下对磁控效果的影响.研究表明,不同壁面导电性下霍尔效应的影响规律不同.绝缘壁面条件下,考虑霍尔效应后壁面热流的变化是附面层内洛伦兹力的变化与激波层厚度的减小二者共同作用的结果.B0=0.2 T时洛伦兹力增加附加的流体减速作用占主导,磁控热防护效果优于忽略霍尔效应的情况,并且在霍尔系数为5.0达到最优;而当B0=0.5 T时,激波层变薄对附面层外缘温度的增加占主导,磁控热防护效果变差,并且随霍尔系数的增加壁面热流越来越大.导电壁面条件下,随着霍尔系数的增加,磁控激波以及热防护效果变差,且当β>5.0时,磁控热防护系统几乎完全失效.

磁流体控制,热防护,霍尔效应,耦合计算

1 引 言

随着飞行器种类逐渐增多、飞行弹道日趋多样,高超声速飞行器在临近空间飞行时的气动热环境越来越恶劣,使得常规热防护手段已不能解决日益严峻的热防护问题[1].得益于超导技术的进步以及相关电磁流动控制机理的研究进展[2,3],磁控热防护技术近年来得到了各国科研机构的广泛关注[4].俄罗斯高温研究所的Bityurin小组[5]、美国空军Bisek小组[6]、日本Yoshino小组[7]以及欧洲航天局的Gulhan小组[8],Cristofolini小组等[9]均对其进行了大量研究,在一定程度上证明了磁控热防护技术的可行性.然而,该技术的实际应用仍然存在许多亟待研究的问题,特别是霍尔效应现象需要深入研究.实际飞行条件下,外加磁场后感应产生的霍尔电场会使得电流出现三维效应,出现流向及法向电流分量,进而改变洛伦兹力,影响磁控热防护系统的效率[10].

目前关于霍尔效应的影响的研究结果并不一致.一部分学者认为,霍尔效应在再入飞行条件下较为显著,不管壁面导电性如何都无法实现有效的激波控制效果[11].另一部分则认为,霍尔效应对磁控效果的影响和壁面导电性密切相关:绝缘壁面条件下,外加磁场仍可以增厚激波层并降低表面热流;导电壁面条件下,外加磁场和等离子流的相互作用几乎完全消失,不再可能降低表面热流.这部分学者以Otsu[12],Fujino[13]和Konigorski[10]为代表.Matsuda等[14]采用试验方法对上述两种结果进行了试验研究,结果表明外加磁场增厚激波层的效果和模型表面的导电性密切相关,采用绝缘壁面比采用导电壁面的激波层增厚效果明显.

尽管Fujino和Otsu的研究结果占主流,但该研究结果基于特定的非平衡霍尔系数模型且只研究了在一个特定大小驻点磁感应强度(B0=0.5 T)下的霍尔效应,存在一定的局限性.另外,简单的由某个工况下的化学非平衡模型确定霍尔系数可能并不能很好地理解霍尔效应的作用机理.况且现有的热化学反应模型在计算电离反应速率时存在不确定性,这给霍尔系数β的计算带来较多的不确定性.为了更好地研究整个再入过程中霍尔效应的作用机理,有必要对霍尔系数β进行参数化研究.虽然Konigorski进行过部分霍尔系数参数化研究,但其采用了完全气体假设,不可避免地同样存在局限性.因此,本文在采用非平衡磁流体控制方程的前提下,不再采用非平衡模型确定霍尔系数β,而是将其简化为一个均一的常数.通过霍尔电场和热化学非平衡流场的耦合求解,研究不同均布霍尔系数、不同驻点条件下霍尔效应对磁控效果的影响,从而获得对该机理的深刻认识,以指导磁控热防护系统设计.

2 物理模型与控制方程

2.1 物理模型

图1给出了磁控热防护(MHD)系统霍尔效应分析的物理模型,磁铁位于飞行器内部的轴线上.磁控热防护系统中,考虑霍尔效应后,感应电场E对波后电子的作用,会使等离子体电导率呈现各向异性,从而使得感应电流出现三维效应.从图1中可以看出,考虑霍尔效应后,除周向电流Jθ外,还出现了法向分量Jn和流向分量Jf.除周向电流Jθ和磁场作用产生的逆流向洛伦兹力Ff外,Jf与磁场相互作用会产生周向的洛伦兹力Fθ.在该周向洛伦兹力的作用下,波后出现速度uθ的周向流动.对磁控热防护而言,逆流向洛伦兹力减速流体的作用至关重要,而考虑霍尔效应后产生的周向洛伦兹力使得流体周向旋转的作用则是无用功.分析霍尔效应对磁控效果的影响,本质上是分析考虑霍尔效应后波后流场内电流以及洛伦兹力各个分量的变化.

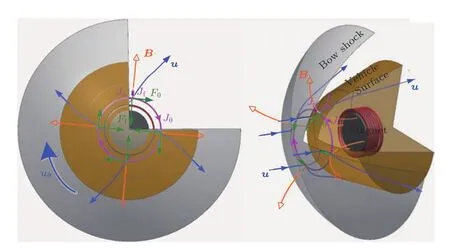
图1 (网刊彩色)磁控热防护系统霍尔效应分析物理模型Fig.1.(color online)Physical model MHD heat shield system for Hall effect analysis.

2.2 控制方程

针对高超声速飞行器前缘流动特点,电磁场和流场耦合分析采用低磁雷诺数假设下的热化学非平衡MHD控制方程[15,16],如(1)式所示.其中,热化学非平衡模型采用Park双温度模型,化学反应动力学模型采用11组元20反应的Gupta模型.

式中U为守恒变量,F,G,H分别为x,y,z方向的对流通量矢量,Fv,Gv,Hv为三方向上的黏性通量项,W为化学反应和振动能量源项矢量,具体表达式见参考文献[17].相对于热化学非平衡黏流,上述方程增加了一个电磁源项矢量SMFD[18]:

可见方程组除流场参数外额外引入了四个变量电流密度J、电场强度E、磁感应强度B以及电磁能量分配比γ.γ表征不同非平衡模式间的电磁能量分配.γ∈[0,1],这里取γ=0.5[18].磁感应强度B在给定磁场形态后即可确定,而考虑霍尔效应后,感应场强E可以通过求解电势泊松方程得到.高超声速飞行器定常绕流条件下,外加稳定磁场时,磁场和感应电场的变化通常都可以忽略不计.因此,可以对安培-麦克斯韦公式、法拉第定律进行简化,将对感应场强矢量E的求解转化为对标量电势ϕ的求解,结合广义欧姆定律可以得到关于ϕ的电势泊松方程[18]:

其中速度矢量u由流场计算得到,电导率张量可以由下式求出:

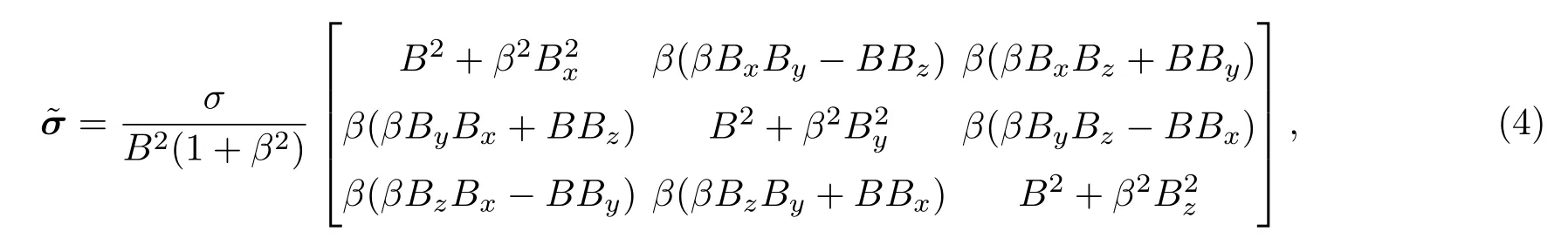
其中,B为磁感应强度矢量B的模;β为霍尔系数,采用均布霍尔系数模型,假设流场区域内霍尔系数为定值;σ为标量电导率,采用如下的非平衡流电导率模型进行计算,

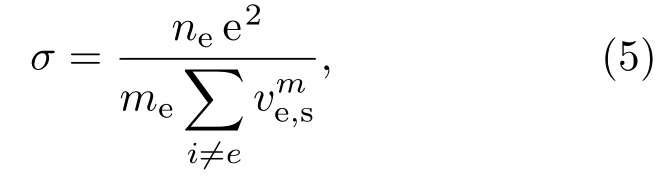
其中,e,ne,me分别为电子电量、电子数密度、电子质量;为电子和其他组元的有效动量传输碰撞频率[19].得到场强E后,电流密度J可由广义欧姆定律确定,至此方程封闭.

3 数值方法与验证

3.1 数值方法

基于上述方程,编写了热化学非平衡条件下的磁流体并行计算程序.流场求解采用有限差分法,而霍尔电场求解采用单元中心有限体积法.其中,流动方程(1)中对流项差分采用AUSMPW格式,隐式求解采用了LU-SGS格式,并且对电磁源项采用了隐式处理以削弱源项过大带来的刚性,从而提高收敛性.电势泊松方程(3)求解采用近似因子交替隐式分解法(AF-ADI),并采用了当地虚拟步进因子法提高了电势迭代的收敛性.霍尔电场的边界条件:绝缘壁面,J·n=0;导电壁面,ϕ=0;其余边界为Neumann边界,∇ϕ·n=0.为提高耦合计算效率,以外加磁场、非平衡流场的耦合收敛解作为三场(磁场、电场、流场)耦合计算的初场.耦合计算开始后,流场每迭代1000步求解一次电场.计算电场时,首先依据流场计算得到的u,ci,ne,TV以及磁场B确定电导率张量˜σ.电势场收敛后,可由电势梯度得到电场场强E,进而由欧姆定律确定感应电流密度J.之后代入流动控制方程进行非平衡磁流体流场求解,直至流场和电场均收敛,计算完成.

3.2 电场计算验证

电场验证算例取自参考文献[18],其控制方程为∆ϕ=xez.该方程拥有解析解ϕ=xez.若令则其控制方程可以化为和(3)式同样的简化形式.给定Dirichlet边界条件:ϕ=xez.计算网格采用局部加密的正方体网格,如图2所示.计算域为x=[0,1],y=[0,1],z=[0,1].从图3可以看出,数值解和解析解符合良好,验证了数值方法对不同网格的适应性.

图2 电场计算验证算例网格Fig.2.Calculation mesh of the electric field validation case.

图3 (网刊彩色)验证算例数值解和解析解对比Fig.3.(color online)Comparison of numerical and analytical results.

3.3 热流计算验证

为验证程序在外加磁场作用下非平衡气动热计算的准确性,选用日本1996年发射的轨道再入试验飞行器(oribital reentry experiment,OREX)1/4前体作为计算模型.流场计算域及边界设置如图4所示. 选取再入飞行时间在7471.5 s(Ma=17.61,H=59.6 km)的飞行工况,并采用了有限催化(PCW,γ=5.0×10−3)壁面模型进行了气动热数值模拟.外加磁场形态同参考文献[20]一样采用磁偶极子磁场.图5给出了三种外加磁场(B0=0,0.3,0.5 T)下表面热流分布曲线.通过与Fujino计算结果[20]的比较可以看出,本文程序计算得到的表面热流和参考文献在三种外加磁场条件下的结果符合良好,验证了本文外加磁场作用下的非平衡气动热数值模拟的准确性.

图4 (网刊彩色)OREX流场计算域(单位/mm)Fig.4.(color online)Calculation mesh and boundary conditions of OREX(in mm).

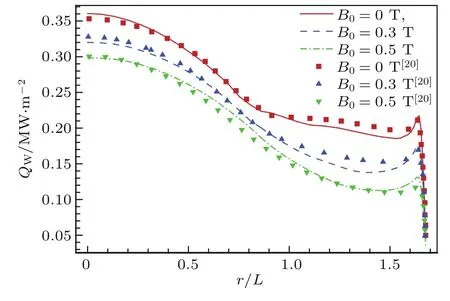
图5 (网刊彩色)三种外加磁场情况下的表面热流分布曲线Fig.5. (color online)Heat fluxes along the wall under three different stagnation magnetic induction strengths(B0=0,0.3,0.5 T).

4 结果与分析

选取OREX再入飞行时间在7461.5 s的飞行工况(Ma=20.04,H=63.60 km),该工况下气动热问题最为严重.两组驻点磁感应强度B0=0.2,0.5 T.壁面条件采用等温全催化壁,并分别采用导电和绝缘壁面以分析不同壁面导电性下霍尔效应的影响.霍尔系数采用1.0—10.0之间的均布霍尔系数模型.

4.1 B0=0.2 T

4.1.1 绝缘壁面

图6(a)给出了绝缘壁面条件不同均布霍尔系数下的表面热流分布.可以看出,绝缘壁面条件下,考虑霍尔效应后,磁控热防护效果优于忽略霍尔效应的情况(除肩部区域外);随着霍尔系数的增加,驻点区表面热流先降低(β<5.0)后增加(β>5.0),磁控效果在β=5时存在最优值.从图6(b)的压力等值线对比可以看出,绝缘壁面条件下考虑霍尔效应的激波脱体距离接近无霍尔效应的情况.图7给出了绝缘壁面条件下洛伦兹力矢量对比.可以看出,随着霍尔系数的增加,激波内侧洛伦兹力降低.β<5.0时在近壁面逆流向洛伦兹力增加与激波脱体距离增加的双重作用下,驻点区表面热流降低明显;当β>5.0时近壁面逆流向洛伦兹力继续增加,但激波脱体距离减小对近壁面温度梯度的增加作用占主导,热流略微增加.

图8给出了绝缘壁面不同均布霍尔系数下的电流密度和电流流线分布.可以看出,随着霍尔系数的增加,感应电流密度峰值下降,周向平面内电流流线大涡逐渐减小,流线方向趋向于垂直壁面.图9给出了XY平面内洛伦兹力分布.可以看出,绝缘壁面条件下,考虑霍尔效应后,激波层内洛伦兹力峰值减小,并出现周向分量,但洛伦兹力的主要方向仍然指向激波外侧,并且当β>5.0时,峰值洛伦兹力不再出现在激波内侧.

图6 (网刊彩色)不同均布霍尔系数下的壁面热流和压力等值线对比(B0=0.2 T,绝缘壁) (a)壁面热流;(b)压力等值线Fig.6.(color online)Heat fluxes and pressure cont ours under different Hall parameters(B0=0.2 T,insulating wall):(a)Heat fluxes;(b)pressure contours.

图7 (网刊彩色)不同均布霍尔系数下的洛伦兹力矢量对比(B0=0.2 T,绝缘表面)Fig.7.(color online)Lorentz forces under different Hall parameters(B0=0.2 T,insulating wall).

图8 (网刊彩色)不同均布霍尔系数下的电流密度分布(B0=0.2 T,绝缘表面) (a)β=0;(b)β=1.0;(c)β=5.0;(d)β=10.0Fig.8.(color online)Electric density contours and streamlines under different Hall parameters(B0=0.2 T,insulating wall):(a)β=0;(b)β=1.0;(c)β=5.0;(d)β=10.0.

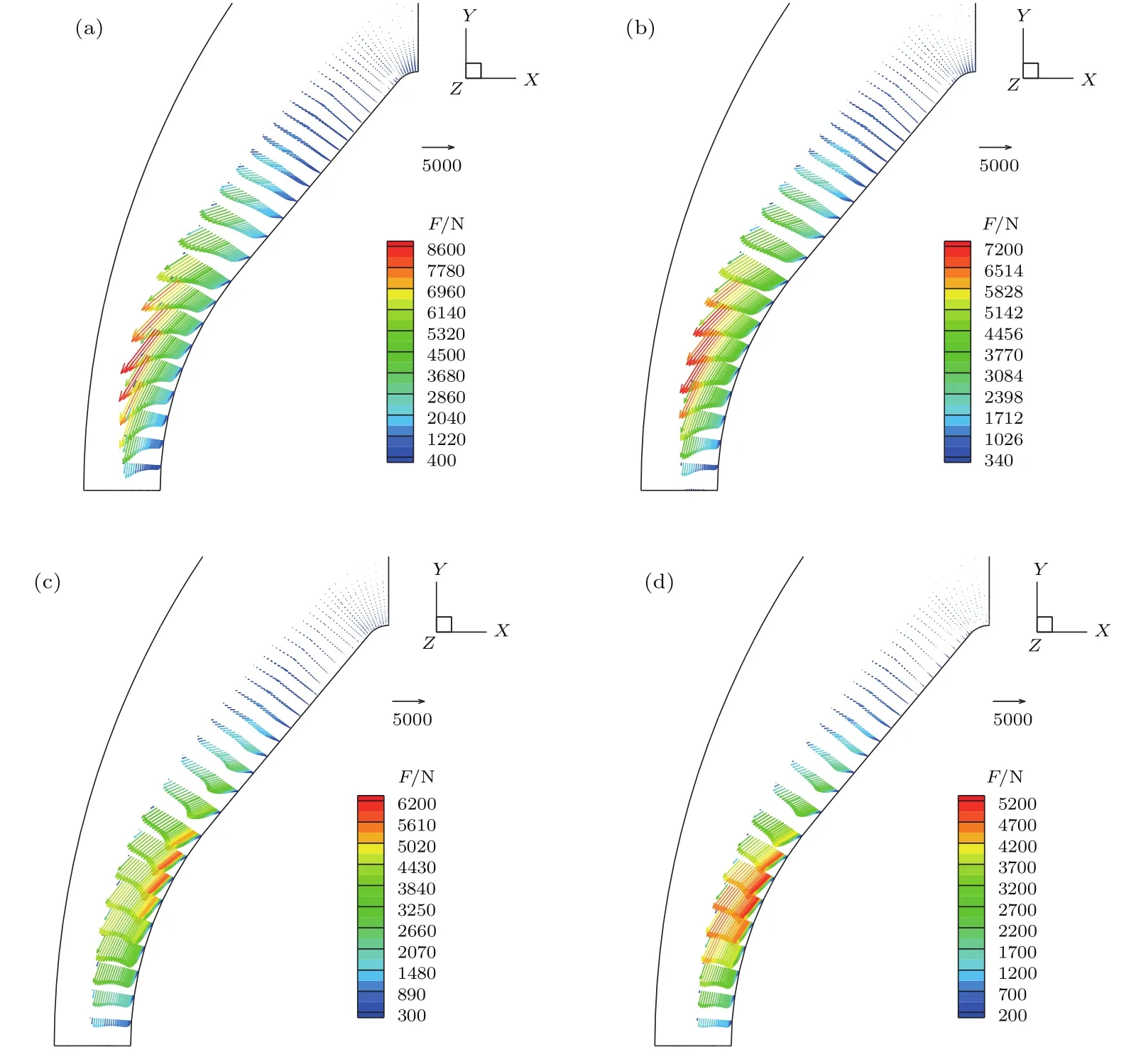
图9 (网刊彩色)不同均布霍尔系数下的XY平面内洛伦兹力矢量分布(B0=0.2 T,绝缘表面) (a)β=0;(b)β=1.0;(c)β=5.0;(d)β=10.0Fig.9.(color online)Lorentz forces on the XY plane under different Hall parameters(B0=0.2 T,insulating wall):(a)β=0;(b)β=1.0;(c)β=5.0;(d)β=10.0.

4.1.2 导电壁面

图10给出了导电壁面条件不同均布霍尔系数下的表面热流分布和压力等值线分布.可以看出,导电壁面条件下,随着霍尔系数的增加,磁控热防护效果变差,且当霍尔系数β>5.0时,激波脱体距离和表面热流趋于稳定,接近无外加磁场情况.

图10 (网刊彩色)不同均布霍尔系数下的壁面热流和压力等值线对比(B0=0.2 T,导电壁) (a)壁面热流;(b)压力等值线Fig.10.(color online)Heat fluxes and pressure contours under different Hall parameters(B0=0.2 T,conductive wall):(a)Heat fluxes;(b)pressure contours.

图11给出了导电壁面不同均布霍尔系数下的电流密度和电流流线分布.可以看出,导电壁面条件下,存在电流“短路”现象,周向平面内电流流线由驻点区壁面发出,而后在肩部流入壁面.此时,随着霍尔系数的增加,感应电流密度峰值迅速下降.从图12的洛伦兹力矢量分布还可以看出,随着霍尔系数的增加,激波层内洛伦兹力逆流向分量减小,周向分量增加,且当β=5.0,10.0时周向洛伦兹力占主导.

4.1.3 绝缘壁面

图13(a)给出了绝缘壁面不同均布霍尔系数下的表面热流分布.可以看出,考虑霍尔效应后,在绝大部分位置绝缘壁面热流高于忽略霍尔效应的情况,并且随着霍尔系数的增加驻点区以及肩部区的磁控防热效果越来越差.霍尔系数为1.0,5.0,10.0情况下,驻点热流相对于忽略霍尔效应情况下分别增加2.6%,8.7%,18.9%.从图13(b)的压力等值线对比可以看出,绝缘壁面条件下,考虑霍尔效应的激波脱体距离接近无霍尔效应的情况,并且随着霍尔系数的增加,激波内侧洛伦兹力降低,激波脱体距离减小.

图14给出了绝缘壁面条件下洛伦兹力矢量和附面层温度的对比.可以看出,随着霍尔系数的增加,激波内侧洛伦兹力降低,附面层减速流体的洛伦兹力增加;但与B0=0.2 T时不同的是,此时激波层变薄对附面层外缘温度的增加占主导,附面层温度梯度变大,磁控热防护效果劣于无霍尔效应情况.

4.1.4 导电壁面

图15给出了导电壁面条件不同均布霍尔系数下的壁面热流和压力等值线分布.可以看出,导电壁面条件下考虑霍尔效应后,随着霍尔系数的增加,磁控热防护效果变差,并且当霍尔系数β>5.0时,驻点区表面热流和激波脱体距离接近于无外加磁场情况,和B0=0.2 T时情况相同.

图11 (网刊彩色)不同均布霍尔系数下的电流流线分布(B0=0.2 T,导电表面) (a)β=1.0;(b)β=5.0;(c)β=10.0Fig.11.(color online)Electric density contours and streamlines under different Hall parameters(B0=0.2 T,conductive wall):(a)β=1.0;(b)β=5.0;(c)β=10.0.

图12 (网刊彩色)不同均布霍尔系数下洛伦兹力矢量分布(B0=0.2 T,导电表面) (a)β=1.0;(b)β=5.0;(c)β=10.0Fig.12.(color online)Lorentz forces on the XY plane under different Hall parameters(B0=0.2 T,conductive wall):(a)β=1.0;(b)β=5.0;(c)β=10.0.

图13 (网刊彩色)不同均布霍尔系数下的壁面热流和压力等值线对比(B0=0.5 T,绝缘壁) (a)壁面热流;(b)压力等值线Fig.13.(color online)Heat fluxes and pressure contours under different Hall parameters(B0=0.5 T,insulating wall):(a)Heat fluxes;(b)pressure contours.

图14 (网刊彩色)不同均布霍尔系数下的洛伦兹力矢量和附面层平动温度分布对比(B0=0.5 T,绝缘表面)(a)洛伦兹力矢量;(b)附面层平动温度分布Fig.14.(color online)Lorentz force vectors and transitional temperature profile of the boundary layer under different Hall parameters(B0=0.5 T,insulating wall):(a)Lorentz force vectors;(b)translational temperature profile.

图15 (网刊彩色)不同均布霍尔系数下的壁面热流和压力等值线对比(B0=0.5 T,导电壁) (a)壁面热流;(b)压力等值线Fig.15.(color online)Heat fluxes and pressure contours under different Hall parameters(B0=0.5 T,conductive wall):(a)Heat fluxes;(b)pressure contours.

图16给出了导电壁面条件下洛伦兹力矢量对比.可以看出,此时随着霍尔系数的增加,洛伦兹力下降,并且当霍尔系数β>5.0时,洛伦兹力下降较多,和B0=0.2 T情况一致.此外,从图17的焦耳热分布可以看出,此处壁面附近焦耳热较大(正值代表焦耳热源为流场供给热量),不利于该位置的热防护,这是图15(a)中β=5.0时在X/L=1.2位置附近表面热流出现突增现象的原因.

图16 (网刊彩色)不同均布霍尔系数下的洛伦兹力矢量对比(B0=0.5 T,导电表面)Fig.16.(color online)Lorentz force vectors under different Hall parameters(B0=0.5 T,conductive wall).

图17 (网刊彩色)XY平面内导电壁面条件下焦耳热分布(B0=0.5 T,β=5.0)Fig.17.(color online)Joule heat contours on the XY plane(B0=0.5 T,β=5.0).

5 结 论

针对高超声速磁控热防护系统的霍尔效应现象,建立了热化学非平衡流场与电磁场的多场耦合数值求解方法.在进行数值方法验证之后,基于变均布霍尔系数模型分析了霍尔效应在不同磁场强度(B0=0.2,0.5 T)、不同壁面条件下(导电、绝缘)对磁控效果的影响.得到以下结论.

1)绝缘壁面条件下,考虑霍尔效应后洛伦兹力的变化与激波层厚度的变化对壁面热流均有影响作用.在不同磁感应强度下(B0=0.2,0.5 T),霍尔效应对壁面热流的影响规律不同.B0=0.2 T时,考虑霍尔效应后附面层洛伦兹力增加,附加的流体减速作用占主导,磁控热防护效果优于忽略霍尔效应的情况,并且在β=5.0达到最优.而当B0=0.5 T时,激波层变薄对附面层外缘温度的增加占主导,磁控热防护效果变差,并且随霍尔系数的增加壁面热流越来越大.

2)导电壁面条件下,随着霍尔系数的增加,磁控热防护效果以及磁控激波变差,逐渐趋近于无外加磁场情况.当霍尔系数β>5.0时,法向洛伦兹力下降较多,周向洛伦兹力占主导,磁控激波和热防护效果大幅减弱,激波脱体距离和表面热流趋于稳定.

以上结论显示,壁面导电性对磁控热防护系统的效能影响巨大.大霍尔系数导电壁面情况下磁控系统几乎安全失效,因此实际应用中飞行器壁面应采用绝缘性能良好的材料.此外,即使采用绝缘壁面,在较强磁场(B0=0.5 T)情况下,磁控效果也明显变弱.可见,磁控系统在应用过程中除了“磁控饱和”现象以外,霍尔效应也是其外加磁场强度不能过大的一个原因.

[1]Zhu Y J,Jiang Y S,Hua H Q,Zhang C H,Xin C W 2014Acta Phys.Sin.63 244101(in Chinese)[朱艳菊,江月松,华厚强,张崇辉,辛灿伟2014物理学报63 244101]

[2]Zhao G Y,Li Y H,Liang H,Hua W Z,Han M H 2015Acta Phys.Sin.64 015101(in Chinese)[赵光银,李应红,梁华,化为卓,韩孟虎2015物理学报64 015101]

[3]Tian Z Y,Zhang K P,Pan S,Li H 2008Chin.Quar.Mechan.29 72(in Chinese)[田正雨,张康平,潘沙,李桦2008力学季刊29 72]

[4]Zhang S H,Zhao H,Du A M,Cao X 2013Sci.China:Tech.Sci.43 1242(in Chinese)[张绍华,赵华,杜爱民,曹馨2013中国科学:技术科学43 1242]

[5]Bityurin V A,Bocharov A N52nd Aerospace Sciences MeetingNational Harbor,Maryland,January 13–17,2014 AIAA 2014-1033

[6]Bisek N J,Gosse R,Poggie J 2013J.Spacecraft Rockets50 927

[7]Yoshino T,Fujino T,Ishikawa M 201041st Plasmadynamics and Lasers ConferenceChicago,Illinois,June 1–28,2010

[8]Gulhan A,Esser B,Koch U,Siebe F,Riehmer J,Giordano D 2009J.Spacecraft Rockets46 274

[9]Cristofolini A,Borghi C A,Neretti G,Battista F,Schettino A,Trifoni E,Filippis F D,Passaro A,Baccarella D 201218th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies ConferenceTours,France,September 24–28 2012,AIAA 2012-5804

[10]Otsu H,Konigorski D,Abe T 2010AIAA J.48 2177

[11]Matsushita K 2003Ph.D.Dissertation(Tokyo:University of Tokyo)

[12]Otsu H,Matsushita K,Konigorski D,Funaki I,Abe T 2004AIAA2004-2167

[13]Fujino T,Matsumoto Y,Kasahara J,Ishikawa M 2007J.Spacecraft Rockets44 625

[14]Matsuda A,Kawamura M,Takizawa Y,Otsu H,Konigorski D,Sato S,Abek T 200745th AIAA Aerospace Sciences Meeting and ExhibitReno Nevada,January 8–11 2007

[15]Lü H Y,Lee C H 2010Chin.Sci.Bull.55 1182(in Chinese)[吕浩宇,李椿萱 2010科学通报 55 1182]

[16]Li K,Liu W Q 2016Acta Phys.Sin.65 064701(in Chinese)[李开,刘伟强 2016物理学报 65 064701]

[17]Liu J 2004Ph.D.Dissertation(Changsha:National University of Defense Technology)(in Chinese)[柳军2004博士论文(长沙:国防科技大学)]

[18]Bisek N J 2010Ph.D.Dissertation(Michigan:University of Michigan)

[19]Gnoffo P A,Gupta R N,Shinn J L 1989 NASA TP-2867

[20]Fujino T,Ishikawa M 2006IEEE Trans.Plasma Sci.34 409

PACS:47.40.Ki,47.85.L–,52.30.Cv,41.20.Gz DOI:10.7498/aps.66.054701

Investigation of Hall effect on the performance of magnetohydrodynamic heat shield system based on variable uniform Hall parameter model∗

Li KaiLiu Jun†Liu Wei-Qiang

(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)

18 September 2016;revised manuscript

6 December 2016)

There has been a resurgence in the field of magnetohydrodynamic(MHD)flow control in the past 20 years.An increasing demand for sustained hypersonic flight and rapid access to space,along with numerous mechanical and material advances in flight-weight MHD technologies,has aroused renewed interest in this subject area.As a novel application of MHD flow control in the thermal protection field,MHD heat shield system has been proved to be of great intrinsic value by lots of researchers in recent years.Although its theoretical feasibility has been validated,there are many problems that remain to be further investigated.Among those problems,the Hall effect is a remarkable one that may affect the effectiveness of MHD flow control.Considering the fact that it is not sufficient to evaluate the Hall effect by merely using the chemical reaction model implemented in the nonequilibrium flow simulation to calculate the Hall parameter,a parametric study is conducted under the assumption of simplified uniform Hall parameter.First,coupling numerical methods are constructed and validated to solve the thermochemical nonequilibrium flow field and the electro-magneticfield.Second,a series of numerical simulations of the MHD head shield system is conducted with different magnitudes of Hall parameter under two magnetic induction intensities(B0=0.2 T,0.5 T).Finally,the influence of Hall effect on the performance of MHD heat shield system is analyzed.Results indicate that Hall effect is closely related to the wall conductivity.If the vehicle surface is regarded as an insulating wall,the heat flux variation is co-determined by varying the Lorentz forces within the boundary layer and the shock-control effect.Compared with the one neglecting the Hall effect,the heat flux with Hall effect is slightly mitigated as the increase of Lorentz forces in the boundary layer dominates when the stagnation magnetic induction intensityB0equals 0.2 T.However,the heat flux is increased whenB0equals 0.5 T,because the decrease of shock stand-o ffdistance dominates which increases the gas temperature outside the boundary layer.Moreover,in this case the larger the Hall parameter,the higher the heat flux will be.As for the conductive wall,the performance of MHD heat shield system becomes worse with the increase of Hall parameter,and while it is equal to or higher than 5.0,this system loses its effectiveness.

magnetohydrodynamic flow control,thermal protection,Hall effect,coupling analysis

PACS:47.40.Ki,47.85.L–,52.30.Cv,41.20.Gz

10.7498/aps.66.054701

∗湖南省自然科学基金(批准号:13JJ2002)和国家自然科学基金(批准号:90916018)资助的课题.

†通信作者.E-mail:liujun@nudt.edu.cn

*Project supported by the Natural Science Foundation of Hunan Province,China(Grant No.13JJ2002)and the National Natural Science Foundation of China(Grant No.90916018).

†Corresponding author.E-mail:liujun@nudt.edu.cn