一类食饵捕食者模型的分支分析

刘 永,赵维锐

(武汉理工大学 理学院，湖北 武汉 430070)

一类食饵捕食者模型的分支分析

刘 永,赵维锐

(武汉理工大学 理学院，湖北 武汉 430070)

针对食饵捕食者问题，研究了具有广义Holling IV型功能反应食饵捕食者模型。在适当的条件下，该模型可能具有一个退化的正平衡点和一个非退化的正平衡点。以描述捕食者变化的两个变量作为分支参数，进行分支分析。当参数发生变化时，在退化平衡点的附近该食饵捕食者系统产生了一个Bogdanov-Takens分支。利用标准型理论和隐函数定理，得到了Bogdanov-Takens分支中鞍结点分支曲线、Hopf 分支曲线和同宿轨道分支曲线的近似表达式。

Bogdanov-Takens分支；退化平衡点；Holling IV型功能反应；食饵捕食者模型

0 引言

食饵捕食者之间的动态关系一直是生物学和生物数学领域的一个重要课题，吸引了国内外很多学者的关注。文献[1-4]详细研究了如下形式的食饵捕食者系统：

(1)其中：x(t)和y(t)分别为食饵和捕食者在时刻t的种群密度；p(x)为功能反应函数；r为食饵的固有增长率；K为环境容量；s为捕食者的增长率；h为反应捕食者种内竞争的正常数。考虑到环境中随机因素的影响，文献[5]提出了具有时滞和随机项的食饵捕食者模型，并得到了系统全局稳定的条件。利用Euler-Maruyama方法可以得到随机种群模型的数值解，并且数值解均方收敛于解析解[6]。

本文研究了具有广义Holling IV型功能反应[7]的食饵捕食者模型，即：

(2)

其中：r,K,a,s,h为正常数；b为任意常数。在详细讨论之前，进行尺度放缩：

(3)

1 Bogdanov-Takens分支的存在性

(4)

其中：x∈(0,1)。注意到方程(4)是1个一元三次方程，在区间(0,1)可能有1个、2个或者3个正解与之对应，系统(3)可能有1个、2个或者3个正平衡点。系统(3)在E(x,y)处的雅可比矩阵为：

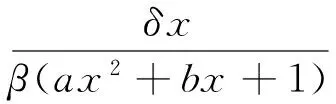
显然，若det(J(E))≠0，E(x,y)是一个非退化平衡点；若det(J(E))<0，则E(x,y)是一个鞍点;若det(J(E))=0，则E(x,y)是一个退化平衡点。对于平衡点的数目和类型，类似于文献[8]，有以下的引理1。

引理1 设

则以下结论成立：

(Ⅰ)若Δ>0，则系统(3)有1个唯一的正平衡点E*=(x*,y*)。

(Ⅱ)若Δ=0并且

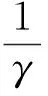
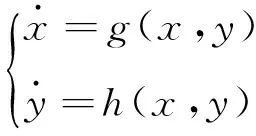
证明 因为(x0,y0)是平衡点，故x0是以下方程的解：

f(x)=g(x,y(x))=0，

其中：y(x)是由h(x,y)=0在x=x0处确定的隐函数，对h(x,y)=0关于x求导，可得：

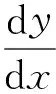
f(μ)=0,f′(μ)=0。

由此可得：

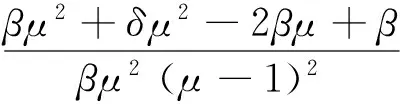
(5)

并且，系统(5)具有两个正平衡点：

2 Bogdanov-Takens分支

选取δ,β作为分支参数，当δ,β发生变化时，研究系统(3)的分支情况，即考虑如下的系统：

(6)

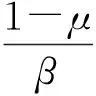
(7)

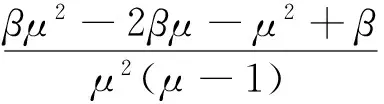
首先，作一个仿射变换：

y1=x1，y2=α10x1+α01x2，

则系统(7)可以写成如下形式：

(8)

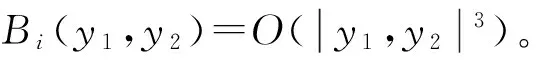
结合系统(8)，可得：

(9)

现在，在原点(0,0)的小邻域内作一个光滑的坐标变换：

X1=z1,X2=z2+C1(z1,z2)，

则系统(9)转化成如下形式 ：

(10)

(11)

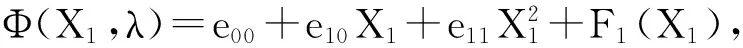
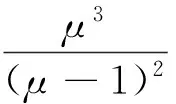
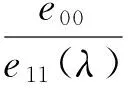
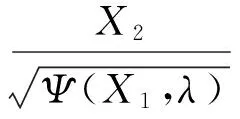
则系统(11)可以写成如下形式：

(12)

(13)

其中：

R(x,y,λ)是关于x,y的幂级数，并且任意一项xiyj满足i+j≥3,j≥2。可以验证:

因此，以上的参数变换是非奇异的，并将对应的eij代入，则系统(13)变成如下形式:

(14)

(15)

选择μ1和μ2作为分支参数，可得:当(λ1,λ2)在原点附近变化时，系统(14)产生了一个Bogdanov-Takens分支。结合隐函数定理，在原点分支曲线的局部表示如下(为了方便起见，记f1=2β(μ-1)2-μ3-μ2,f2=β(μ-1)2-μ3)。

(Ⅰ)鞍结点分支曲线：

曲线SN包含SN+和SN-两部分，其中，SN+={(λ1,λ2):μ1(λ1,λ2)=0,μ2(λ1,λ2)>0}，SN-={(λ1,λ2):μ1(λ1,λ2)=0,μ2(λ1,λ2)<0}。

(Ⅱ)Hopf分支曲线：

(Ⅲ)同宿轨道分支曲线：

综上所述，有以下的定理：

3 结束语

[1] HUANG J,RUAN S,SONG J.Bifurcations in a predator-prey system of Leslie type with generalized Holling type III functional response[J].Journal of differential equations,2014,257(6):1721-1752.

[2] CAI L,CHEN G,XIAO D.Multiparametric bifurcations of an epidemiological model with strong Allee effect[J].Journal of mathematical biology,2013,67(2):185-215.

[3] LI Y,XIAO D.Bifurcations of a predator-prey system of Holling and Leslie types[J].Chaos,solitons & fractals,2007,34(2):606-620.

[4] BRAZA P A.The bifurcation structure of the Holling-Tanner model for predator-prey interactions using two-timing[J].SIAM journal on applied mathematics,2003,63(3):889-904.

[5] 聂文静,王辉,胡志兴,等.一类具有时滞和随机项的捕食-被捕食模型[J].河南科技大学学报(自然科学版),2015,36(6):75-81.

[6] 郭书东,张启敏.跳扩散种群系统的数值解[J].河南科技大学学报(自然科学版),2009,30(5):89-92.

[7] ANDREWS J F.A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates[J].Biotechnology and bioengineering,1968,10(6):707-723.

[8] XIAO D,RUAN S.Global analysis in a predator-prey system with nonmonotonic functional response[J].SIAM journal on applied mathematics,2001,61(4):1445-1472.

[9] CHOW S N,HALE J K.Methods of bifurcation theory[M].Heidelberg:Springer Science & Business Media,2012.

[10] PERKO L.Differential equations and dynamical systems[M].Heidelberg:Springer Science & Business Media,2013.

国家自然科学基金项目(11601402);湖北省自然科学基金项目(2013CFB347)

刘永(1990-),男,安徽蒙城人,硕士生;赵维锐(1967-),男,湖北恩施人,教授,博士,硕士生导师,主要研究方向为动力系统.

2016-05-30

1672-6871(2017)02-0089-06

10.15926/j.cnki.issn1672-6871.2017.02.017

O193

A