具有时变时延的不确定非线性系统的跟踪控制

孟 宇,李庆奎

(山西大学 数学科学学院,山西 太原 030006)

具有时变时延的不确定非线性系统的跟踪控制

孟 宇,李庆奎

(山西大学 数学科学学院,山西 太原 030006)

针对一类具有时变时延的不确定非线性系统的跟踪控制问题，利用扩张状态观测器估计系统中具有时变时延的未知项。对于在反推技术中出现虚拟控制的导数，采用非线性跟踪微分器对其进行跟踪，设计实际控制器以使闭环系统中的状态及部分跟踪信号收敛于原点邻域。仿真结果验证了该方法的可行性。

扩张状态观测器；微分跟踪器；反推技术；跟踪控制

0 引言

近年来,非线性系统的镇定和跟踪问题得到了广泛关注[1-3]。非线性系统的镇定强调系统的状态收敛于系统原点的邻域内，而跟踪问题主要有状态跟踪和输出跟踪。目前，虽然对非线性系统输出跟踪控制问题的研究已有很多[4-6]，但是时延作为实际系统中普遍存在的现象，很大程度上会影响系统的稳定性。因此，对具有时变时延的非线性系统的跟踪控制问题的研究更有意义。

自适应反推设计是解决非线性系统的一种方法[7]。此外,对于系统中的不确定项，有些学者选用径向基函数神经网络或模糊逻辑系统来逼近未知非线性函数[8-9]。但是，随着系统阶和时变时滞的增加，这类系统的控制设计问题变得更加复杂，自抗扰控制技术可有效解决该类问题[10-11]。文献[10]针对一类具有外部扰动的不确定非仿射纯反馈非线性系统,通过将系统中的未建模动态和未知项看作一个未知综合扰动，对这个未知综合扰动进行实时估计和补偿。但是上述文献只考虑了不确定的存在，并没有考虑实际系统中不可避免的时变时延。

本文研究了具有时变时延的非线性系统跟踪控制问题。首先，将具有时变时延的未知非线性项看作不确定项。然后，结合自抗扰控制技术和反推方法，针对每个子系统中不确定项，通过建立扩张状态观测器对其进行估计。而对于在每一步反推设计中出现的虚拟控制的导数,为了使问题简单化，本文采用跟踪微分器对其进行跟踪。最后，通过仿真实例验证了本文方法的有效性。

1 问题的描述和准备

考虑一类具有时变时延的不确定非线性系统，可表示为：

(1)其中：∑i为第i个子系统；x=[x1,x2,…,xn]∈Rn为系统的状态；gi为正常数；hi(xi(t))为已知函数；fi(xi(t-di(t)))为具有时变时延di(t)的未知光滑非线性函数,i=1,2,…,n；u(t)∈R,y(t)∈R分别为控制输入和系统输出。

本文的控制目标：对于具有时变时延的非线性系统，利用反推技术设计控制器，使得系统的输出y(t)跟踪参考信号yr，且最终闭环系统的状态及部分跟踪信号 (对不确定项的跟踪以及对虚拟控制导数的跟踪) 保持有界。需要作如下假设：

假设1 当xi(t)≠0,i=1,2,…,n，fi(xi(t-di(t)))连续可微，其微分有界且不为0。

假设2 系统的所有状态是可测的。

为了实现对信号导数的估计,选择非线性跟踪微分器为：

(2)

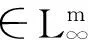
2 主要结果

在利用反推技术设计控制器之前，先介绍自抗扰的概念。考虑如下不确定非线性系统：

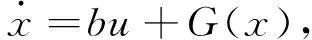
(3)

其中：G(x)为光滑不确定非线性函数。不失一般性，假设状态可测，将G(x)看作是扰动项，可将系统(3)扩展为：

其中：H(x)是未知的，且为G(x)的导数。

然后，为系统(3)构建扩展状态观测器，如下式：

其中：Z2→G(x)。则可设计如下控制器使得系统镇定：

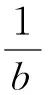
其中：k>0为待设计的常数。

引理1 通过为系统(3)构建二阶扩展状态观测器，可设计控制器使系统(3)渐近稳定。

证明 将控制器代入系统(3)，可得：

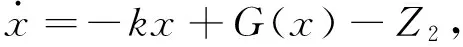
利用基于扩张状态观测器和跟踪微分器的反推方法，设计系统(1)的控制器。

步骤1 考虑子系统∑1，定义变量z1=y-yr，对z1求导可得：

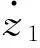
(4)

由于f1(x1(t-d1(t)))是未知函数，使用扩张状态观测器对未知量进行估计。在假设1和假设2成立的条件下，构建扩张状态观测器，如下式：

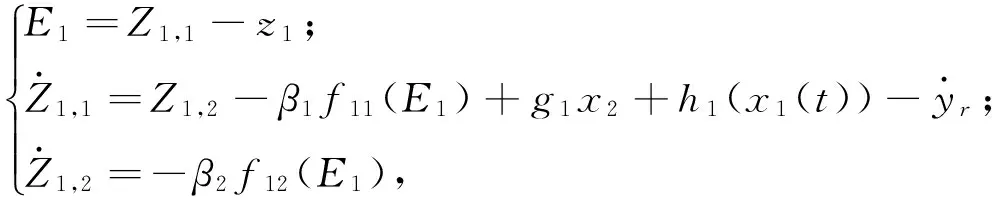
(5)

其中：Z1,1、Z1,2为扩张状态观测器的状态；β1、β2为适当参数；f1j(E1),j=1,2为满足条件E1f1j(E1)≥0的适当非线性函数。

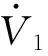
(6)

定义变量z2=x2-x2d，将其代入扩张状态观测器(5)可得：

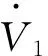
(7)

(8)

假设z2=0，f1(x1(t-d1(t)))-Z1,2可被看作是干扰，则式(8)可变为：

(9)

由输入到状态稳定性定理可知，若z2=0时，系统(4)是输入到状态稳定的。也就是说只要f1(x1(t-d1(t)))-Z1,2有界，那么z1就有界。

步骤2 对变量z2求导，可得：

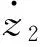
(10)

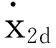
(11)

(12)

其中：Z2,1、Z2,2为扩张状态观测器的状态；β1、β2为适当参数；f2j(E2),j=1,2为满足条件E2f2j(E2)≥0的适当非线性函数。

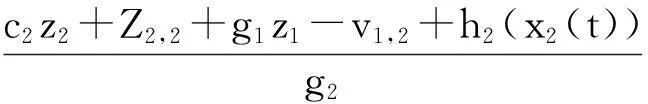
可选Lyapunov函数为V2=V1+V21，对其进行求导并整理可得：

(14)

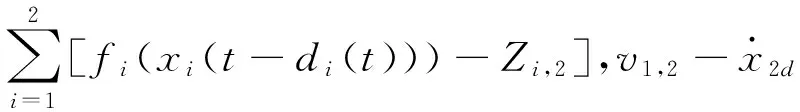
(15)

步骤i对zi=xi-xid进行微分得：

(16)

(17)

(18)

其中：Zi,1、Zi,2为扩张状态观测器的状态；β1、β2为适当参数；fij(Ei),j=1,2是满足条件Eifij(Ei)≥0的适当的非线性函数。

定义变量zi+1=xi+1-xi+1,d，同时可设计如下虚拟控制器：

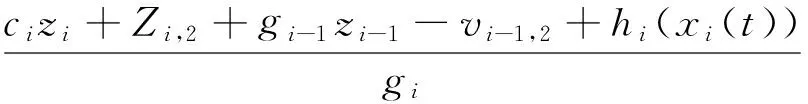
(19)

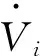
(20)

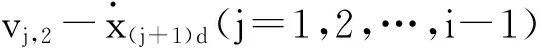
步骤n对zn=xn-xnd进行微分得：

(21)

(22)

建立扩张状态观测器：

(23)

其中：Zn,1、Zn,2为扩张状态观测器的状态；β1、β2为适当参数；fnj(En),j=1,2为满足条件Enfnj(En)≥0的适当非线性函数。

根据以上步骤可设计实际控制器为：

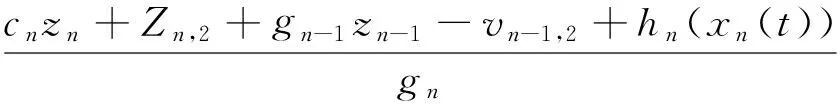
(24)

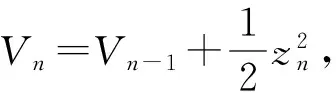
(25)

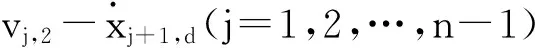
注1 本文的扩张状态观测器选自文献[10]。只要选取适当参数β1、β2和非线性函数fi,1(Ei)、fi,2(Ei)(i=1,2,…,n)，扩张状态观测器对多数系统都能估计出其状态变量。

定理1 系统(1)在满足假设1和假设2的情况下，可以通过设计虚拟控制器和实际控制器，使得闭环系统的状态渐近收敛到原点的邻域内且输出信号跟踪参考信号。

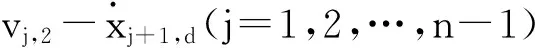
(26)

那么式(25)可以变为：

(27)

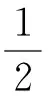
3 仿真例子

为了证明本文方法的有效性，选取系统如下：

其中：g1=3.0;g2=10.9;时变时延d1(t)=1-0.5cost;时变时延d2(t)=1-0.5sint。取参考信号yr=0.5sint+sin(0.5t)，设初始值为x1(0)=2,x2(0)=-2。扩张状态观测器和跟踪微分器的参数可选为：β1=255,β2=0.2,ω=3.5。仿真图见图1～图4。图1给出了系统输出x1与参考信号yr随时间变化曲线。图2为跟踪微分器的状态v1,1及虚拟控制x2d的时间响应曲线，证明其跟踪效果很好。图3为扩张状态观测器状态Z1,2及非线性项f1的时间响应曲线，图4是扩张状态观测器状态Z2,2及非线性项f2的时间响应曲线。由图3和图4可知：扩张状态观测器的状态可以很好地估计未知非线性项。分析图1～图4可知：本文的设计方法有效。

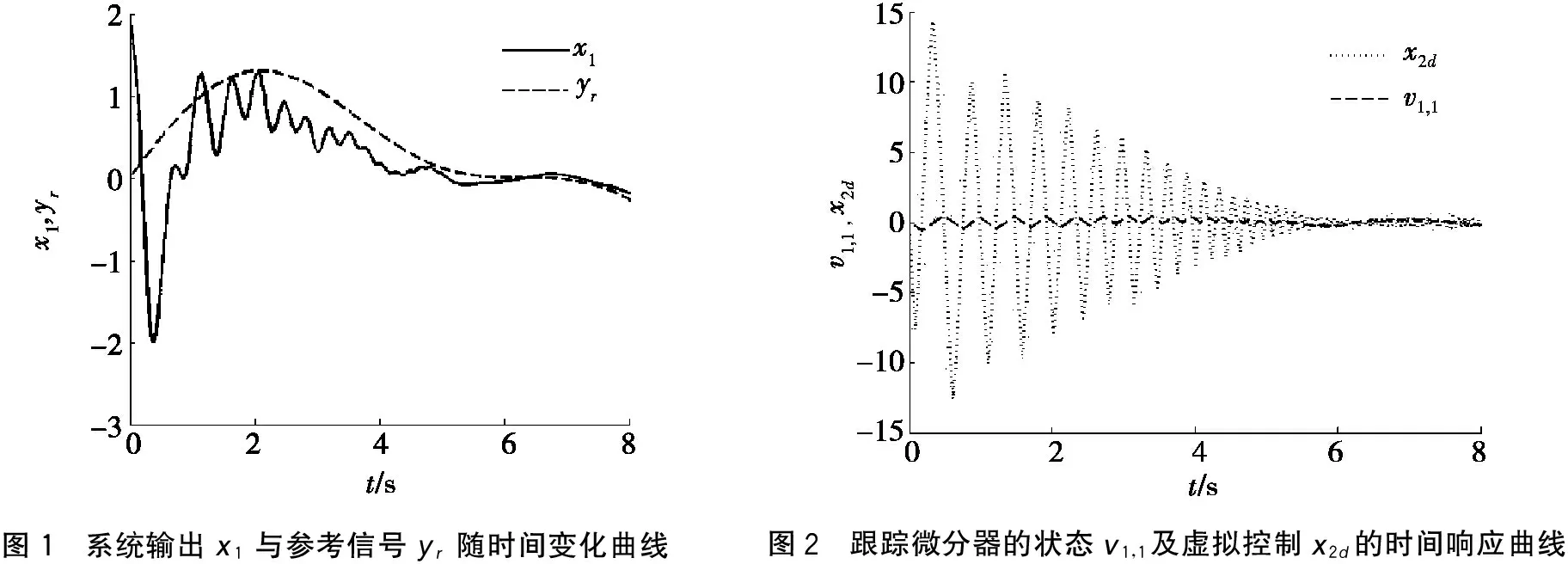
图1 系统输出x1与参考信号yr随时间变化曲线图2 跟踪微分器的状态v1,1及虚拟控制x2d的时间响应曲线

4 结论

本文针对一类具有时变时延的不确定非线性系统的跟踪控制问题，通过将具有时变时延的未知非线性项看作不确定项，利用扩张状态观测器的状态实时估计系统中的不确定项，使用反推技术逐步得到实际控制器。对于在反推技术中出现的虚拟控制的导数，利用跟踪微分器对其进行跟踪。仿真结果验证了本文设计方法的有效性。

[1]LIF,LIUY.Globalstabilizationviatime-varyingoutput-feedbackforstochasticnonlinearsystemswithunknowngrowthrate[J].Systems&controlletters,2015,77:69-79.

[2]JIANGPJ.Multiple-targetstrackingcontrolalgorithmforaclassofnonlinearsystemswithfeedforwardcompensations[J].Neurocomputing,2016,196:210-213.

[3] 张铎,马照瑞,朱训林.非均匀采样非线性系统的模糊控制器设计[J].河南科技大学学报(自然科学版),2016,37(4):50-55.

[4]LAIGY,LIUZ,PHILIPCCL,etal.Adaptiveasymptotictrackingcontrolofuncertainnonlinearsystemwithinputquantization[J].Systems&controlletters,2016,96:23-29.

[5]WULB,YANGGH.Adaptivefuzzytrackingcontrolforaclassofuncertainnonaffinenonlinearsystemswithdead-zoneinputs[J].Fuzzysets&systems,2016,290:1-21.

[6]ZHANGZQ,XUSY,ZHANGBY.Exacttrackingcontrolofnonlinearsystemswithtimedelaysanddead-zoneinput[J].Automatic,2015,52(52):272-276.

[7]LIY,TONGS,LIT.Adaptivefuzzybacksteppingcontroldesignforaclassofpure-feedbackswitchednonlinearsystems[J].Nonlinearanalysishybridsystems,2015,16:72-80.

[8]HUAC,FENGG,GUANX.Robustcontrollerdesignofaclassofnonlineartimedelaysystemsviabacksteppingmethod[J].Automatic,2008,44(2):567-573.

[9]ZHOUQ,WUCW,JINGXJ,etal.Adaptivefuzzybacksteppingdynamicsurfacecontrolfornonlinearinput-delaysystems[J].Neurocomputing,2016,199:58-65.

[10]CHENGCH,HUYA,WUJH.Autodisturbancecontrollerofnon-affinenonlinearpurefeedbacksystems[J].Actaautomaticsinica,2014,40(7):1528-1536.

[11]CHENGCH,HUYA,WUJH,etal.Outputtrackcontrolofchaoticsystemwithuncertaintyandnon-affineinputs[J].TransactionofBeijinginstituteoftechnology,2014,34(4):386-391.

国家自然科学基金项目(61573230);山西省回国留学人员科研基金项目(2015-017)

孟宇(1990-),女,山西忻州人,硕士生;李庆奎(1971-),男,通信作者,山东郯城人,副教授,博士,硕士生导师,主要研究方向为切换时滞系统、网络控制系统及供应链系统.

2016-08-21

1672-6871(2017)02-0048-06

10.15926/j.cnki.issn1672-6871.2017.02.009

TP13

A