基于马尔科夫—灰色BP神经网络组合模型的深基坑变形预测研究
2017-07-31袁继雄
刘 洁,吴 鸣,袁继雄
(1.汕头大学工学院,广东 汕头 515063;2.汕头市政府投资项目代建管理中心,广东 汕头 515000)
LIU Jie1,WU Ming1,YUAN Jixiong2
(1.Department of Civil Engineering,Shantou University,Shantou 515063,Guangdong,China; 2.Shantou Government Investment Project Construction Management Centre,Shantou 515000,Guangdong,China)
基于马尔科夫—灰色BP神经网络组合模型的深基坑变形预测研究
刘 洁1,吴 鸣1,袁继雄2
(1.汕头大学工学院,广东 汕头 515063;2.汕头市政府投资项目代建管理中心,广东 汕头 515000)
建立马尔科夫—灰色BP神经网络组合模型是为了更加科学合理预测深基坑压顶水平位移,提高预测精度.比较分析BP神经网络模型与串联式灰色BP模型的预测结果,建立马尔科夫链修正的灰色BP组合模型,以汕头市某花园酒店扩建工程的基坑压顶水平位移的实测数据为研究对象,通过比较模型预测结果与实际结果,检验其深基坑预测模型的精度.实例证明,经马尔科夫链改进的灰色BP神经网络组合模型的预测精度优于单一模型,更适合用于样本少、随机波动性大的深基坑变形预测.马尔科夫—灰色BP神经网络组合模型对深基坑压顶水平位移的预测不仅精度高,同时反映出数据序列发展变化的总体趋势和系统之间各状态的规律,为深基坑压顶水平位移预测提供了一种新方法.
马尔科夫链;灰色BP神经网络;深基坑;预测
0 引言
我国沿海地区广泛分布软土地基,其本身所具有的独特的地质、水文特征更使基坑工程的安全控制难度大大增加.由于深基坑开挖引起地表沉降、周围建筑物倾斜的例子已屡见不鲜,工程的安全问题已引起全社会的关注.因此,在基坑施工过程中建立基坑变形监测系统,通过监测数据检验基坑运行时各种设计参数是否符合要求,预测基坑未来的变形,对控制基坑工程施工过程,保证基坑及周边环境的安全具有重要指导意义.王鸣翠等[1]结合灰色理论建立非等时距灰色GM(1,1)模型对深基坑变形进行了预测,取得良好效果;黄传胜等[2]为预测深基坑开挖变形建立了灰色新陈代谢GM(1,1)模型和灰色马尔科夫链模型;刘戈等[3]利用灰色模型和BP神经网络组合对样本少、信息量不足情况下的深基坑进行预测;薛鹏松等[4]利用马尔科夫修正灰色神经网络组合模型对水质进行预测,提高了灰色神经网络的预测精度.综上所述,灰色系统预测预报模型以计算简便而著称,但其只能作单步预测,因此在建筑基坑预测预报中应用并不多;采用灰色神经网络的模型来分析波动大、复杂性高、非线性变化的数据,最终拟合结果与实测结果相差过大;采用马尔科夫修正的灰色神经网络只是对等时距灰色神经网络模型进行预测,对非等时距模型的预测还有待研究.虽然神经网络在基坑变形预测方面已取得一些成果,但其缺乏系统性、全面性,有必要进一步探讨改进灰色神经网络模型的方法.
本研究通过灰色GM(1,1)非等时距模型得到基坑压顶水平位移的预测数据,对灰色残差序列利用BP神经网络修正得到灰色BP神经网络残差值,对组合模型的残差进行马尔科夫修正,建立用于基坑压顶水平位移预测的马尔科夫—灰色BP神经网络组合模型.
1 模型介绍
1.1 非等时距灰色GM(1,1)模型灰色系统是中国学者邓聚龙在1982年最早创立的一种研究少数据、贫信息不确定性问题的新方法[5].灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,其特点是所需样本少,模型简单.GM(1,1)模型是灰色系统中应用最广泛的一种模型.根据其建模机理、计算过程和方法,将非等时距灰色GM(1,1)预测模型的建模步骤[6]归纳如下:
(1)一次累加生成数列设监测得到的实际序列数据为:

其中,如果间距Δki不是一个常数,则该序列为非等时距序列.对x(0()k)作一次累加生成数据:

其中


式中,a,b为灰参数,它们可通过如下辨识算法求得:

式中

将式(4)代入式(3)中可得GM(1,1)模型的时间响应函数为:

(3)通过上式计算出xˆ(1()k)i,作数据还原处理,可得到按模型计算的序列xˆ(0()ki+1).其数据还原公式为:

其中xˆ((0)2),…,xˆ((0)n)为回代检验的数列部分;xˆ(0()n+1),xˆ((0)n+2),…为预测值数列部分.(4)最后计算残差.残差:e(k)i=x(0()k)i-xˆ(0()k)i(7)相对残差:q(k)i=e(k)i/x(0()k)i(8)
1.2 BP神经网络模型
神经网络BP算法是一种有监督的学习方式,其运算机理如下:对n个学习样本P1,P2,…,Pn,对应的目标样本T1,T2,…,Tn,学习的目的是用网络的实际输出A1,A2,…An与目标输出T1,T2,…,Tn之间的误差来修改权值,它是通过不断在相对误差函数斜率下降的方向上计算权值和误差变化而逐渐逼近目标值的.BP算法由信息的正向传输和误差的反向传输两部分构成,考虑到计算效率问题,本文采用带一个隐含层的3层BP网络模式对基坑压顶WY15号水平位移进行模拟预测.其含有隐含层的网络结构图如图1.

图1神经网络结构图
1.3 灰色BP神经网络组合模型
灰色预测模型的优点是短期预测,缺点则是对长期和波动性较大的数据拟合较差,神经网络具有较强的局部逼近和非线性预测能力,而收敛速度慢,易陷入局部极小是BP神经网络自身的问题.灰色系统与神经网络的融合实现了优势互补[8],将灰色GM(1,1)模型与BP神经网络模型按串联式组合,使模型同时适用于少样本情况,也可使数据序列的信息充分利用,提高整体趋势的泛化能力.本文采用BP神经网络对灰色模型进行残差修正,建立灰色模型与BP网络串联式组合模型.其原理是先建立灰色GM(1,1)预测模型,得到模拟值,从而得到残差序列{e(i)},i=1,2,…,n,将数列{e1,e2,e3},{e2,e3,e4},…,{e(n-6),e(n-5),e(n-4)}作为网络的输入样本,输出样本为{e4,e5,…,e(n)},即为等维新息BP网络模型,等维新息是根据灰色理论中的新陈代谢来处理数列,用BP网络模型对残差序列e(i)进行预测得到新的序列{e'(i)}.然后得到新的预测值:

其中,xˆ(0)(i)为灰色模型的预测值.
1.4 马尔科夫链修正的灰色BP神经网络组合模型
马尔科夫链是一种特殊的随机过程,根据系统当前时刻的状态推出下一时刻的状态概率分布,从而得到下一时刻的状态[9].马尔科夫链预测的结果为一范围,适合于对波动性较大的预测问题进行修正.即马尔科夫—灰色BP组合模型其原理如下:
(1)将灰色BP组合模型所得到的残差序列划分为n个状态.
(2)确定状态转移概率与状态转移矩阵,若Mij(m)为由状态i经过m步转移到状态j的原始数据样本数,Mi为处于状态i的原始数据样本数,则:

i=1,2,…,n.Pij(m)即为状态转移概率,马尔科夫一步转移概率矩阵用P(1)表示.P(1)=[P11(1),…,P1n(1);…;Pn1,…,Pnn(1)],则m步概率转移矩阵P(m)=[P(1)]m.
(3)对一步转移概率矩阵P(1),设预测对象处于k状态,若maxP(1)kj=P(1)k1,则可认为下一时刻系统最有可能由状态k转向状态1,若矩阵P(1)中第k行有两个或两个以上概率相同时,则需要考察二步或n步转移概率矩阵.
(4)马尔科夫—灰色BP组合模型的预测结果[10]:Y=y/(1-q),其中y为灰色BP模型的预测值,q为原状态空间的分界值.
2 模型应用
以汕头市某花园酒店扩建工程为例,其基坑支护结构侧壁安全等级各向均为二级,开挖面积约为7 800 m2,开挖深度为8.45 m.该基坑周边环境较为复杂.北面距离小区路中线11.5 m,距离现有建筑物最近约19 m;东面距离原酒店一期建筑物最近约4.6m;南面距离两层商铺25.7 m;西面距离小区路中线17 m,距离现有建筑物约29.1 m.基坑及周边环境监测点布置图见图2.为确保工程施工期间的安全,以及周围建筑物的安全,根据设计要求,基坑施工应与现场监测相结合,对现场监测所得信息进行分析,及时反馈给设计和施工单位,达到信息化和动态化施工.通过对原始数据的分段优选,本文选取基坑中两个压顶水平位移监测点北面的WY5与南面的WY15两个比较具有代表性的监测点数据进行模型检验和预测分析.
2.1 非等时距灰色BP神经网络组合模型的应用
(1)非等时距灰色GM(1,1)预测模型
以基坑压顶水平位移数据作为输入数据,以原数据序列的初始值作为累加数列的初始值,因灰色模型需要先训练,且需要预留几次实测数据用来验证模型的精确度,所以选用原始数据的前n-3个数据作为训练样本,代入到已建好的灰色GM(1,1)模型进行训练,即可得到模型的测试值及相对误差,将原始序列的最后三个数据作为预测样本,与灰色模型得到的预测值进行比较.WY5、WY15两个监测点的灰色模型测试值和预测值分别见表1、表2.利用残差数据可对所建GM(1,1)模型的精度进行检验,本文采用后验差检验,利用平均残差求得的残差方差与原始数据方差的比值即后验差C,模型精度为p=1-εavg,其中εavg为平均残差.
(2)BP网络模型
采用基坑压顶水平位移WY15、WY5的原始数据作为BP神经网络样本.若输入层包含节点过多,会使计算周期和工作量增大,对模型预测精度也有一定影响,因此选用原始数据的前n-3个位移值作为BP神经网络的训练序列,后3个实测作为预测值,并用Matlab2012b建模.网络拓扑结构为3-13-1,选用tansig传递函数建立网络,采用梯度下降traingd作为训练函数,设置训练精度为0.000 1,训练最大步数为10 000进行训练仿真,求得WY5、WY15的拟合值及相对误差分别见表1、表2.
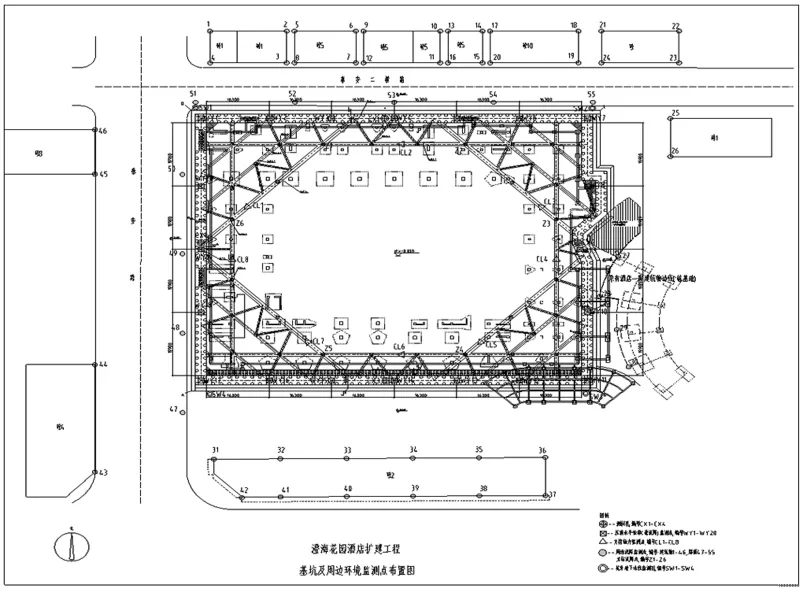
图2基坑及周围环境监测点布置图
(3)非等时距灰色BP神经网络组合模型
将非等时距灰色GM(1,1)模型得到的残差值作为BP神经网络的输入值,经灰色BP神经网络组合模型训练网络,得到WY5、WY15的测试值及预测值分别见表1、表2.
(4)精度检验及分析
将灰色模型、BP神经网络模型及灰色BP神经网络模型得到的相应测试值和预测值与其对应的实测值进行比较,由表1、表2可以看出,在模型测试中,灰色BP神经网络模型的预测精度高于灰色模型和BP网络模型的预测精度,且相对误差均在4%以内.在预测阶段,灰色BP组合模型显示了其优势,由表1可计算出WY5经三种模型得出的平均相对误差绝对值,灰色模型、BP神经网络模型及灰色BP模型预测值的平均相对误差的绝对值分别为3.7%、5.45%、2.43%,由BP神经网络预测的第10次数据精度不高,原因是在第128天时,基坑东北在拆支撑,而点WY5就是基坑东北方的监测点,当发生突变时,单一的BP神经网络预测效果并不理想,而灰色BP神经网络在该点的预测精度较高,相对误差为1.24%.由表2也可以看出单纯的BP神经网络模型对少样本序列的预测精度不高,相比之下,灰色BP模型预测精度高于单一模型.于是,为提高灰色BP模型精度,引入马尔科夫链对模型进行修正,以期获得更好效果.
由图3和图4可以看出,三种模型均可有效地预测两个监测点的预测值,BP神经网络模型在前期的拟合效果比较好,而灰色模型仅在后期预测曲线与实测曲线较接近,灰色BP神经网络模型的预测曲线与实测曲线整体拟合效果较好.灰色BP网络模型预测仅用了10组和11组数据,属于“少样本”、“贫信息”的情况.由此可看出灰色BP神经网络模型充分利用了灰色系统和神经网络各自的优点,对“少样本”、“贫信息”的数据序列可以得到较高的预测精度.

表1 WY5三种模型预测结果对比表

表2 WY15三种模型预测结果对比表

图3 WY5三种模型预测结果比较图

图4 WY15三种模型预测结果比较图
因此,灰色BP神经网络模型在实际工程的预测方面应用广泛.灰色系统和BP神经网络模型的成功组合也表明,可将灰色系统、神经网络、时间序列分析、遗传算法、马尔科夫链等各种分析方法,在一定条件下进行组合也许可以得到很好的效果.针对波动性较大的点,灰色BP网络模型也不能很好处理,由此引入马尔科夫链原理,可针对波动性较大的点利用概率问题进行处理.
2.2 马尔科夫—灰色BP神经网络组合模型的应用
(1)模型计算
由灰色BP神经网络组合模型得到相对误差的绝对值,将其划分马尔科夫的状态区域分别三个状态区间.以此对灰色BP神经网络组合模型的误差进行状态分类,由已建的马尔科夫-灰色BP神经网络模型得WY5、WY15的预测值及相对误差见表3、表4.
(2)精度检验及分析
由表3、表4可知,由马尔科夫—灰色BP神经网络模型得到测试样本的相对误差的绝对值均在0.4%以内,模型预测精度远远高于灰色BP神经网络和单一模型,由该模型得到的预测值的模型相对误差也均在1.5%以内,相对于灰色GM(1,1)模型、BP神经网络模型、灰色BP神经网络组合模型,其模型有较高预测精度.综上所述,马尔科夫—灰色BP神经网络模型在基坑压顶水平位移的预测精度均优于以上三种模型.
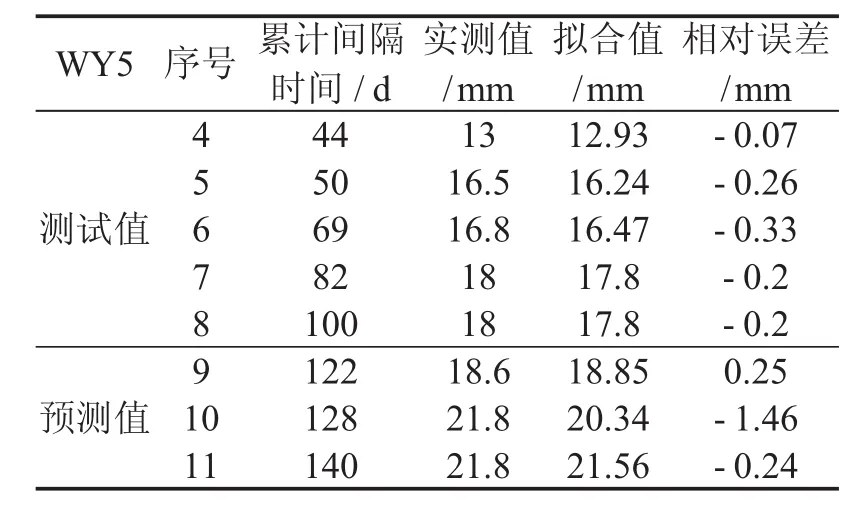
表3 WY5马尔科夫—灰色BP神经网络组合模型预测

表4 WY15马尔科夫—灰色BP神经网络组合模型预测
3 结 论
(1)利用非等间距灰色模型解决了工程中众多利用非等间距时间监测数据进行预测的问题,具有更好的实用价值.BP神经网络模型采用了等维新息方法,使建模序列更能反映系统目前特征.
(2)建立马尔科夫—灰色BP神经网络模型对基坑压顶水平位移进行预测,该模型完成了两次残差修正,通过实例进行模型精度对比,灰色BP神经网络模型和马尔科夫—灰色BP神经网络模型均可进行预测分析,而对基坑压顶水平位移的预测中,马尔科夫—灰色BP神经网络模型各项指标均优于单个模型与灰色BP神经网络模型.本基坑预测方法仅适用于基坑正常开挖条件下,基坑支护形式与深度与本工程相似的情况,对于其他情况的深基坑类型还有待研究.在实际工程中应根据实际情况选择合适的预测模型.
[1]王鸣翠,于胜文,张帅帅,等.基坑变形非等间距灰色预测模型程序设计及应用[J].测绘地理信息,2015,40(1):41-44.
[2]黄传胜,张家生.深基坑开挖变形的灰色马尔科夫链预测方法[J].铁道科学与工程学报,2011,8(2):71-75.
[3]刘戈,仝国柱.基于灰色BP神经网络组合模型的深基坑周围地表沉降预测研究[J].天津城建大学学报,2016,22(3):184-189.
[4]薛鹏松,冯民权,邢肖鹏.基于马尔科夫链改进灰色神经网络的水质预测模型[J].武汉大学学报(工学版),2012,45(3):319-324.
[5]邓聚龙.灰色系统基本方法[M].武汉:华中工学院出版社,1987:96-108.
[6]彭涛,杨岸英,梁杏,等.BP神经网络-灰色系统联合模型预测软基沉降量[J].岩土力学,2005,26(11):1810-1814.
[7]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010.
[8]贾备,邬亮.基于灰色BP神经网络组合模型的基坑变形预测研究[J].隧道建设,2009,29(3):280-283.
[9]JING Y P,ZHANG X,LUO Y.Forecasting of urban water demand based on combining Grey and BP neural network with Markov chain model[J].Journal of Northwest A&F University,2011,39(7):229-234.
[10]景亚平,张鑫,罗艳.基于灰色神经网络与马尔科夫的城市需水量组合预测[J].西北农林科技大学学报(自然科学版),2011,39(7):229-234.
[11]刘志斌,施斌.灰色马尔可夫链在深基坑沉降预测中的应用[J].煤田地质与勘探,2002,30(6):35-37.
Research of Deep Foundation Pits Prediction Based on Combining Markov Chain-Grey and BP Neural Network Model
To scientifically predict deep foundation pit horizontal displacement,a combined model based on Grey and BP neural network model corrected by Markov chain is established to improve accuracy.On the analysis of BP neural network model and the tandem Grey BP model, a prediction model based on Markov chain and Grey BP neural network model is set up.The foundation pit horizontal displacement of a certain garden hotel in Shantou is used to verify the model and check its precision by comparing the model prediction results and the actual results. The result shows that Grey BP neural network and Markov chain have higher precision.It’s more suitable for deep foundation pits prediction with less samples and large stochastic volatility.The Markov chain-Grey BP neural network model is not only giving higher prediction but showing the data sequence trends and the internal law between system states.It provides a newmethod for deep foundation pit deformation prediction.
Markov chain;Grey BP neural network;deep foundation pits;prediction
LIU Jie1,WU Ming1,YUAN Jixiong2
(1.Department of Civil Engineering,Shantou University,Shantou 515063,Guangdong,China; 2.Shantou Government Investment Project Construction Management Centre,Shantou 515000,Guangdong,China)
TU470
A
1001-4217(2017)03-0053-08
2016-10-02
刘 洁(1992—),女,河南商丘人,硕士研究生,研究方向:结构现代维修加固理论和方法研究,E-mail:14jliu@stu.edu.cn
住房和城乡建设部科技计划项目(2015-k3-003)
