检测图像篡改的脆弱水印技术

常玉红，黄惠芬，王志红



检测图像篡改的脆弱水印技术

常玉红，黄惠芬，王志红

（山东英才学院，山东济南 250014）

针对图像篡改取证定位问题，提出利用混沌序列和图像QR分解相结合的脆弱水印算法判定图像篡改情况。该算法选取QR分解实现图像分解，图像分解后嵌入水印，同时利用混沌系统对其加密以增强水印的安全性。实验结果发现，所提算法不仅提高了定位型水印算法的安全性，而且还可以估计被篡改区域的篡改强度。

脆弱水印；混沌；QR分解；篡改

1 引言

随着多媒体处理技术和软件的飞快发展，对数字媒体进行编辑修改变得越来越容易，使人对数字信息的真实性和完整性无法进行认证，如何对数字媒体进行认证变得日益紧迫和重要[1]。在众多媒体中，图像由于其传播量大和直观性很受关注，针对图像篡改取证的研究也成为当前的研究热点。数字图像取证分为主动取证和被动取证，其中，嵌入数字水印方法是图像主动取证的方法之一。数字水印认证系统原理是利用图像存在的冗余数据随机地将水印信息内嵌在原始媒体中，实现水印信息与原始媒体数据融合，二者合成后生成的媒体从视觉上与原始图像无差别，从而起到保护图像真实性和完整性，判定图像是否被篡改的作用。数字水印技术凭借其有效检测数字图像完整性和有效地进行数字版权保护等诸多特性引起很多研究者的关注[2]。用于图像认证的水印主要是脆弱性水印，这种水印嵌入图像后重新被提取，可通过水印的完整性判定图像是否被篡改，还可以根据水印被破坏的位置和程度判断图像被篡改的位置和篡改的程度，实现图像篡改识别和定位以保证内容的真实性。在水印嵌入技术方面，一些研究者提出了很多新的方法，如混沌理论的加密算法、Hash加密算法以及各种SVD分解，QR分解技术相继被应用到水印嵌入技术中。

水印嵌入过程如图1所示，水印提取过程如图2所示。

QR分解在数字水印领域受到密切关注[3~6]。苏庆堂[7]提出了一种高效的基于QR分解的彩色图像盲水印算法，能满足水印的不可见性和一般顽健性的需要。基于QR分解的数字水印算法[9]是目前求一般矩阵全部特征值最有效且广泛应用的方法。Yashar等[8]将图像像素块采取QR分解，在其矩阵第1行嵌入水印信息。混沌是一种复杂的非线性动力学系统[9]，自提出混沌方法以来，在密码领域就少不了混沌的身影。研究人员提出很多利用混沌序列对水印信息进行加密的方法。按照置乱的对象不同，基于混沌理论的加密方法分为2种，文献[10,11]通过产生混沌序列来改变图像中像素的位置。文献[12,13]利用混沌映射产生的混沌序列与像素的灰度值进行逻辑或算术运算使像素的灰度值发生改变。文献[14]最早介绍了如何采用混沌序列处理数字水印的方法。文献[15]为解决多重数字水印的嵌入问题，通过选取不同的Logistic混沌映射初始迭代值而产生不同的迭代序列予以实现。文献[16]提出基于混沌理论和位运算的加密算法。

本文在总结前人技术的基础上，选取与图像内容密切相关的图像QR分解作为嵌入的水印，为了增强水印的安全性，采用混沌系统对其加密，当需要对图像进行认证时，通过比较嵌入前后的水印差值定位图像被篡改的区域位置。

2 相关技术

2.1 矩阵QR分解

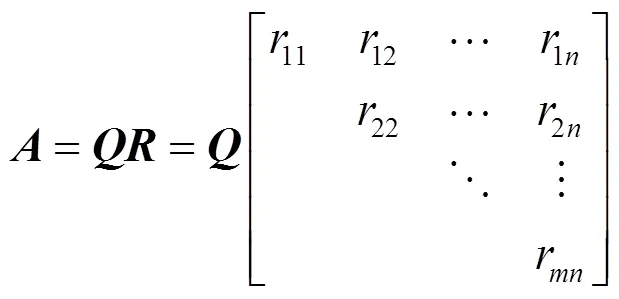
非负矩阵指的是矩阵中的所有元素都是非负的实数。图像可以表示成像素组成的矩阵，它是一个非负矩阵。用表示灰度图像生成的矩阵，则可以表示为的矩阵，其元素的取值范围为[0, 255]。QR分解是把任何阶方阵分解成阶正交矩阵和阶上三角矩阵初等变换形式的乘积。

2.2 混沌序列的散列处理

Logistic映射是非常重要的混沌系统，目前被广泛地用来产生混沌序列。它的优点是生成序列比较容易，具有较强的伪随机性，长期不可预测。方程形式为

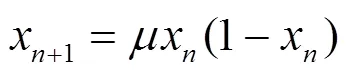
(3)

3 水印生成、嵌入算法和提取过程

3.1 水印生成算法

在图像的传输和处理过程中，接收的含水印图像可能会受到一定的扰动，因此会影响水印的提取，为了分散提取水印的错误比特，从而加强水印的顽健性，同时也为了增强嵌入水印的保密性，在水印嵌入前采用混沌置乱技术生成要嵌入的水印。

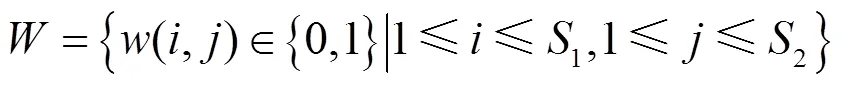
本文采用的置乱方法如下。

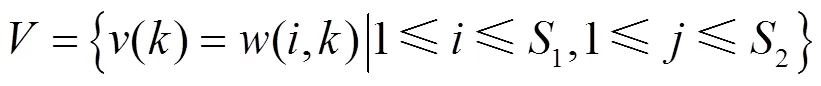
(5)

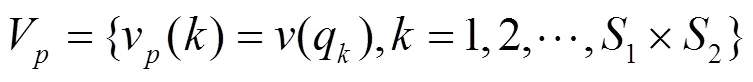
经过散列处理的混沌序列，其置乱映射是一一对应的。

3.2 嵌入水印算法

在图像中嵌入水印的过程步骤如下。

1) 利用Logistic[20]映射函数生成混沌序列，在生成序列的过程中混沌序列的长度由原始图像的大小决定。若原始图像的大小为，水印图像的大小是，二者满足，混沌序列的长度计算为。假设混沌序列表示成，，则可以定义为

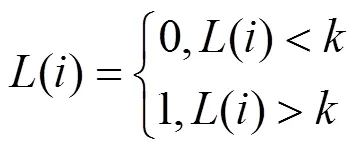
3.3 水印提取算法

从图像中提取水印的过程是嵌入水印过程的逆过程，实现步骤如下。

1) 利用Logistic映射函数的初值和阈值将混沌序列映射成表示的二值序列。

2) 采用与嵌入算法相同的密钥，从含水印图像中选取个像素，并从这个像素提取出最低有效位表示为。

4) 步骤3)提取的8个像素的高7 bit，并取其余像素的8 bit，二者组成二进制序列，与利用密钥生成的序列进行异或运算得到，式为，其中，为图像的像素，为散列表。

从以上步骤可知，在图像被嵌入水印后，若图像没有被改动过，当输入正确的密钥时，含水印图像会通过验证，否则，若图像被改动过或者密钥不正确，图像不会通过验证。

3.4 篡改检测与定位

本算法可对图像进行的恶意篡改进行定位，可以计算原水印和从图像提取的水印的差值，用表示

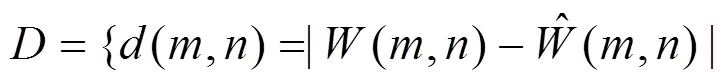
(8)

若用户对已经含水印的图像进行正常处理操作时，差值上错误像素点显现的规律一般是孤立的、稀疏的；若图像受到的是恶意攻击或非法篡改操作，上错误像素点则会呈现出另一种现象，即错误点分布非常密集。由此，可以通过观察差值图像上错误像素点的分布是稀疏还是密集，从主观和客观上评价图像是否被恶意篡改并以此对篡改位置进行定位，还可以进一步确定篡改的区域以及篡改的强度。

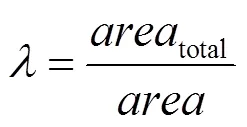
(10)

本文对篡改的判定规则定义如下。

4 实验与分析

4.1 不可见性

嵌入水印算法若合适，嵌入水印后的图像从外观上看不出变化，同时可用峰值信噪比衡量其质量。本文算法采取的办法是在图像每个像素的最低有效位把水印嵌入，平均信噪比大小计算为

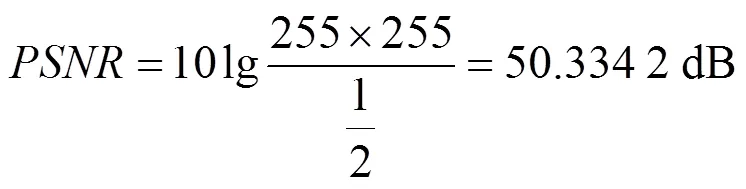
(a) 原始图像 (b) 嵌入水印后图像

图3 图像嵌入水印前后视觉对比

4.2 图像篡改检测与篡改定位

实验对图3中的含水印图像3(b)进行复制粘贴篡改，将一个辣椒添加在图像的右下方，得到如图4(a)所示的图像。实验过程：首先以大小为32×32图像块为一单元生成脆弱水印信息，在密钥的控制下通过几何变换将图像进行4×4的分块置乱，以其中大小为32×32的图像块为一个单元生成脆弱水印信息W,j进行嵌入，若对图像任何一个8×8图像块中的像素进行改动，可利用W,j检测到改动操作，同时利用本文算法都可被脆弱水印检测到实现篡改定位。为了较为直观地表示，将利用脆弱水印W,j进行篡改定位以图像形式表示，结果分别如图4(b)、图4(c)和图4(d)所示，仿真实验来说明本算法具有良好检测能力和定位效果。

(a) 篡改图像 (b) 8×8篡改定位图像

(c) 4×4篡改定位图像 (d) 2×2篡改定位图像

图4 篡改与篡改定位图像

本文算法的密钥空间也可达到127×127，所以攻击者很难采用穷举法获得密钥，算法的安全性得以保证。

5 结束语

本文提出基于QR分解和混沌序列的脆弱水印算法。对图像进行QR分解，分解的图像失真比较小，通过混沌序列分散实现水印信息嵌入图像变换系数中，提高了算法的安全性。仿真实验结果表明，图像受到非法篡改后，通过提取的水印能够精确地进行篡改判断和定位。但在实验中发现本文算法中采用的水印由于其完全脆弱性而不能抵抗压缩，而图像的压缩操作在图像存储、传输过程中是必要的操作之一，这个问题在未来的研究中需要继续深入研究，改进的目标是让本文算法对图像的一些常规操作有一定的顽健性。

[1] 孙圣和, 陆哲明, 牛夏牧, 等. 数字水印技术及应用[M]. 北京:科学出版社, 2004.

SUN S H, LU Z M, NIU X M, et al. Digitao watermarking technology and application[M]. Beijing: Science Press, 2004.

[2] SONG W, HOU J J, LI Z H, et al. Chaotic system and QR factorization based robust digital image watermarking algorithm[J]. Journal of Central South University of Technology, 2011, 18(1): 116-124.

[3] SU Q T, NIU Y G, WANG G, et al. Color image blind watermarking scheme based on QR decomposition[J]. Singal Processing, 2014, 94(1): 219-235.

[4] NADERAHMADIAN Y, HOSSEININ-KHAYAT S. Fast and robust watermarking in still images based on QR decomposition[J]. Multimedia Tools & Applications, 2014, 72(3):2597-2618.

[5] 马晓红, 赵琳琳. 基于QR分解和提升小波变换的顽健音频水印方法[J]. 大连理工大学学报, 2010,(2): 278-282.

MA X H, ZHAO L L. A robust audio watermarking method based on QR decomposition and lifting wavelet transform[J]. Journal of Dalian University of Technology, 2010,(2): 278-282.

[6] 汪萍, 刘粉林, 巩道福. 基于QR分解的数字水印算法数字图像认证方案[P]. GB2011100799133.

WANG P, LIU F L, GONG D F. Digital image watermarking method and digital image authentication method based on QR decomposition[P]. GB2011100799133.

[7] 苏庆堂. 基于盲提取的彩色图像数字水印算法[D]. 上海：华东理工大学, 2013.

SU Q T. Research on blind watermarking scheme of digital color image[D]. Shanghai: East China Unibesity of Science and Technology, 2013.

[8] NADERAHMADIAN Y, HOSSEININ-KHAYAT S. Fast watermarking based on QR decomposition in wavelet domain[C]//2010 Sixth International Conference on Intelligent Information Hiding and multimedia Signal Processing. 2010: 127-130.

[9] 郝柏林. 从抛物线谈起——混沌动力学引论[M]. Shanghai：上海科技教育出版社. 1993.

HAO B L. Talking from parabolic——introduction to chaotic dynamics[M]. Shanghai: Shanghai Science and Technology Education Press.1993.

[10] 易开祥, 孙鑫, 石教英. 一种基于混沌序列的图像加密算法[J]. 计算机辅助设计与图形学学报, 2000, 12(9):672-676.

YI K X, SUN X, SHI J Y. An image encryption algorithm based on chaotic sequences[J]. Journal of computer aided design and computer graphics, 2000, 12(9):672-676.

[11] 赵学峰.一种新的数字图像置乱方案[J].计算机应用研究,2004, (6):112-113.

ZHAO X F. A new scrambling scheme of digital image[J]. Application Research of Computer, 2004(6):112-113.

[12] 袁玲, 康宝生. 基于Logistic混沌序列和位交换的图像置乱算法[J]. 计算机应用, 2009, 29(10):2681-2683.

YUAN L, KANG B S. Image scrambling algorithm based on logistic chaotics equence and bit exchange[J]. Journal of Computer Application, 2009, 29(10):2681-2683.

[13] 张爱华, 江中勤. 基于Logistic映射的混沌图像加密算法的改进[J]. 南京邮电大学学报(自然科学版),2009,29(4):69-73.

ZHANG A H, JIANG Z Q. Improving for chaotic image encryption algorithm based on logistic mapping[J]. Journal of Nanjing University of Posts and Telecommunications(Natura lScience), 2009, 29(4): 69-73.

[14] XIANG H, WANG L D, LIN H, et al. Digital watermarking systems with chaotic sequences[C]//Conference on Security and Watermarking of Multimedia Contents. 1999: 449-457.

[15] 丁科, 何晨, 蒋铃鸽, 等. 基于地址码的脆弱数字水印技术[J]. 上海交通大学学报, 2004, 38(4): 620-623.

DING K, HE C, JIANG L G, et al. A fragile watermark technique based on address code[J]. Journal of Shanghai Jiaotong University, 2004, 38(4): 620~623.

[16] 刘乐鹏, 张雪锋. 基于混沌和位运算的图像加密算法[J]. 计算机应用, 2013, 33(4): 1070-1073.

LIU L P, ZHANG X F. Image encryption algorithm based on chaos and bit operations[J]. Journal of Computer Application, 2013, 33(4): 1070-1073.

[17] 陈善学, 彭娟, 李方伟. 基于二维 Logistic 混沌映射的 DWT 数字水印算法[J]. 重庆邮电大学学报(自然科学版),2012,24(4): 495-500.

CHEN S X, PENG J, LI F W. DWT digital watermarking algorithm based on 2D logistic chaos mapping[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2011, 41(1): 38-41.

Fragile watermarking technique for detecting image

CHANG Yu-hong, HUANG Hui-fen, WANG Zhi-hong

(Shandong Yingcai University, Jinan 250014, China)

Aiming at the problem of image tampering and forensic localization, a fragile watermarking algorithm based on chaos sequence and image QR decomposition was proposed to determine the image tampering. The algorithm chooses QR decomposition to decompose the image, embeds the watermark after the image is decomposed, and encrypts the watermark by chaotic system to enhance the security of the watermark. Experimental results show that the algorithm not only improves the security of the location watermarking algorithm, but also can estimate the tampering strength of the tampered area.

fragile watermarking, chaos, QR decomposition, tamper

TP391

A

10.11959/j.issn.2096-109x.2017.00168

常玉红（1977-），女，山东聊城人，山东英才学院副教授，主要研究方向为信息隐藏。

黄惠芬（1980-），女，山东威海人，博士，山东英才学院教授，主要研究方向为信息隐藏。

王志红（1978-），女，山东泰安人，山东英才学院副教授，主要研究方向为信息隐藏。

2017-01-17；

2017-03-22。

常玉红，sflcycyh@163.com

国家自然科学基金资助项目（No.61402271）；山东省重点研发科技发展计划基金资助项目（No.2015GGX101012,No.2016GGX101037）；山东省自然科学基金资助项目（No.ZR2015JL023, No.ZR2015FL025, No.ZR2016FM34, No.ZR2016FQ23）；山东省社科规划基金资助项目（No.15CXWJ08）；山东省高等学校科研计划基金资助项目（No.J15LN54, No.J16LN55）

The National Natural Science Foundation of China (No.61402271), The Key R & D Technology Development Foundation of Shandong Province (No.2015GGX101012, No.2016GGX101037), The Natural Science Foundation of Shandong Province (No.ZR2015JL023, No.ZR2015FL025, No.ZR2016FM34, No.ZR2016FQ23), The Social Science Planning Project of Shandong Province (No.15CXWJ08), High Education Research Project of Shandong Province (No.J15LN54, No.J16LN55)