自动化搜索ARX分组密码不可能差分与零相关线性闭包
2017-07-31韩亚
韩亚
自动化搜索ARX分组密码不可能差分与零相关线性闭包
韩亚1,2
(1. 中国科学院信息工程研究所信息安全国家重点实验室,北京100093; 2. 中国科学院大学,北京 100049)
首先,构造了ARX分组密码差分特征及线性掩码的传播方程;然后,利用SAT求解器求解传播方程并且判定该传播系统是否为有效传播;最后,遍历差分特征及线性掩码自动化搜索不可能差分及零相关线性闭包。利用该算法搜索TEA、XTEA和SIMON的不可能差分与零相关线性闭包,并得到TEA、XTEA及SIMON族分组密码的最优不可能差分与零相关线性闭包。此外,利用差分以及线性分布表,该算法能有效搜索基于S盒分组密码的不可能差分及零相关线性闭包。
不可能差分;零相关线性;ARX结构;SAT求解器
1 引言
不可能差分分析[1]由Knudsen提出用于分析DEAL分组密码,随后Biham等[2]利用该方法分析Skipjack[2]和IDEA[3]。针对AES[4,5]、CLEFIA[6]和LBlock[7]等分组密码,不可能差分分析已经成为一种行之有效的攻击方法。不可能差分分析利用差分传播概率为零的区分器(不可能差分)筛除错误轮密钥,并通过穷举候选密钥恢复正确密钥。零相关线性分析方法由Bogdanov等[8]第一次提出用于分析分组密码算法。现在,零相关线性分析已经成功应用到CLEFIA[9]、LBlock[10,11]和SIMECK[12]等分组密码中。与不可能差分分析类似,零相关线性分析利用线性传播掩码为零的区分器(零相关线性闭包)筛除错误轮密钥,结合穷举恢复正确密钥。不可能差分分析与零相关线性分析区分器的长度直接决定其攻击轮长度。因此,如何有效地搜索更长更多的不可能差分及零相关线性闭包至关重要。
早期密码研究者利用中间相错法(miss-in- the-middle)搜索不可能差分及零相关线性闭包。2003年,Kim等[13]提出了一种自动化搜索不可能差分的方法——方法,该方法只适用于搜索具有双射轮函数的分组密码算法。2009年,Luo等[14]通过改进方法提出一种搜索不可能差分方法——UID方法。UID方法提出了更一般化的不可能差分判定条件。2012年,Wu等[15]提出了更一般化的自动化搜索不可能差分方法——WW方法。WW方法通过构建轮差分路径传播方程,并通过全部求解线性方程以及部分求解非线性方程判定不可能差分,最后通过穷举输入输出差分自动化搜索分组密码轮不可能差分。由于方法、UID方法以及WW方法不能够有效地刻画差分经过“&”运算以及模加运算的传播方程,因此,这3种方法都不适用于搜索ARX结构分组密码的不可能差分。
ARX结构分组密码轮函数由模加运算(addition)、循环移位运算(rotation)和异或运算(XOR)组成。Lipmaa等[16]给出对数时间算法计算差分特征值经过模加运算的差分传播概率,并给出差分传播以概率1经过模加运算的传播条件。Wallén[17]给出线性掩码经过模加运算的相关系数计算方程,并给出线性掩码以概率1经过模加运算的传播条件。结合Lipmaa和Wallén提出的计算方程,通过构造ARX分组密码差分,线性传播方程,利用求解器的方法实现自动化搜索ARX结构分组密码的不可能差分和零相关线性闭包。
本文利用SAT/SMT求解器,通过构建差分及线性掩码传播方程,自动化搜索ARX结构分组密码的不可能差分及零相关线性闭包。结果如表1所示。
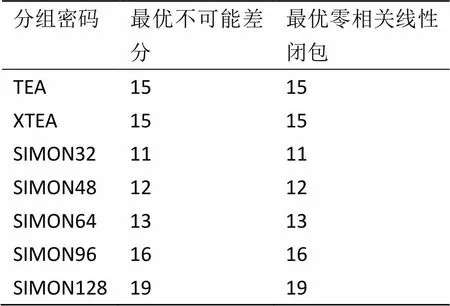
表1 最优不可能差分及零相关线性闭包轮数
2 差分、线性掩码部件传播模型
ARX结构分组密码轮函数包括模加运算、循环移位运算、异或运算和分支操作。差分及线性掩码经过各部件的传播可以通过方程的形式表示。
2.1 模加运算
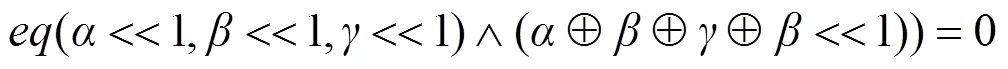
(2)
否则
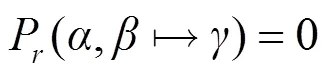
其中
(4)
(5)
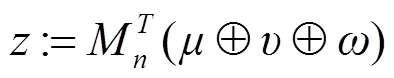
(7)
2.2 循环移位运算
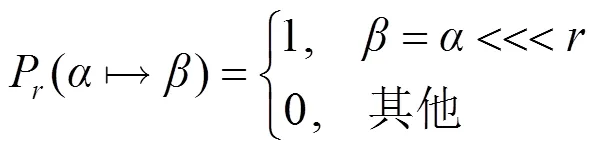
(9)
2.3 异或运算
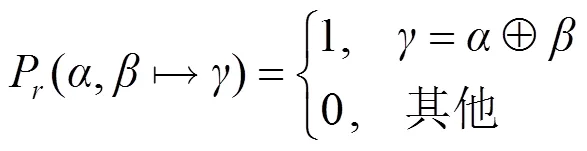
(11)
2.4 分支运算
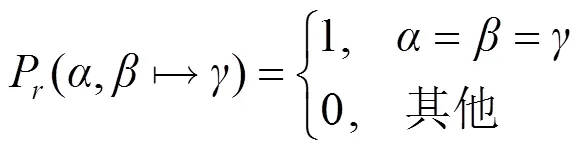
(13)
2.5 类SIMON轮函数
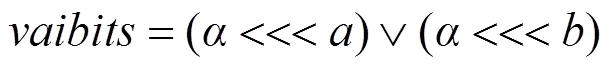
(15)
(16)
则差分传播概率为
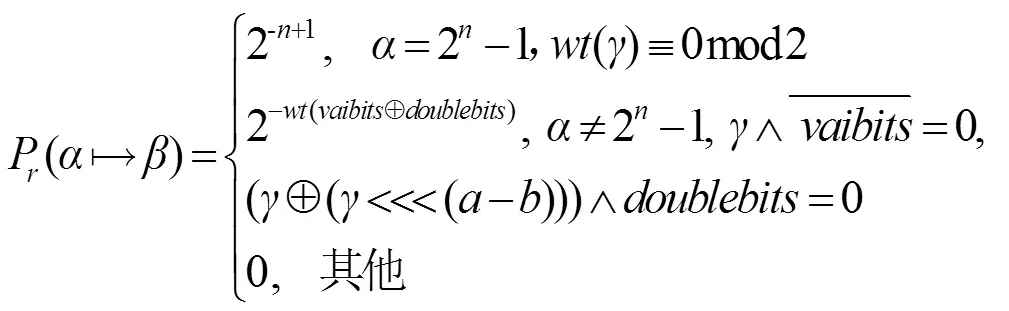
(18)
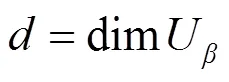
则线性平方相关系数为
(20)
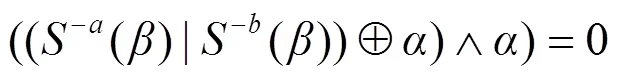
3 算法实现
3) 求解。利用SAT/SMT求解器求解并返回结果。
step 1;
step 2;
step 3;
break;
else
总条数加1;
end if
end for
end for
其中,称step1、step2、step3为一个会话,遍历与的时间复杂度为个会话。当取值较大时,计算机很难实现整个搜索过程。因此,在遍历与时,限制其汉明重量使。因此该算法的时间复杂度约为O(),数据复杂度为O(),空间复杂度为O(1)。当取值为128时,所需时间复杂度约为O(),数据复杂度为O(),空间复杂度为O(1)。

表2 TEA和XTEA分组密码搜索结果
4 应用
4.1 TEA和XTEA
TEA是由Wheeler等[19]提出的一种轻量级分组密码算法。TEA的分组长度为64 bit,密钥长度为128 bit。TEA分组密码轮函数包括模加运算、循环移位和异或运算,轮函数表示为
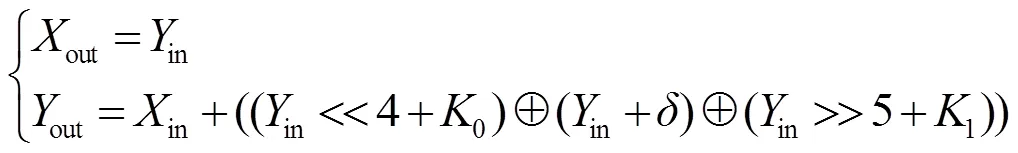
XTEA是Needham等[19]对TEA的一种改进方案,保持了TEA的分组长度和密钥长度,改进了轮函数结构,轮函数表示为
(23)
TEA和XTEA分组密码轮函数如图1所示。
遍历所有输入输出汉明重量为1的差分、线性特征值,利用差分以及线性经过分组密码部件传播模型并结合TEA和XTEA轮函数结构,构建轮差分(线性掩码)传播方程满足差分传播概率(线性掩码相关系数)。解析轮差分(线性掩码)传播方程为SAT求解器识别模型,并判断该条路径是否为不可能差分(零相关线性掩码)。该搜索算法对TEA和XTEA分组密码的搜索结果如表2所示。
4.2 SIMON
SIMON[20]是NSA提出的轻量级分组密码算法。SIMON是类Feistel结构分组密码,其分组长度为,表示为SIMON2n,字长度。SIMON分组密码轮函数表示为
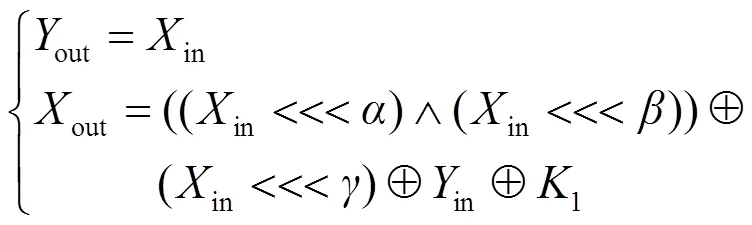
循环移位常数,,。SIMON分组密码轮函数如图2所示。
利用该搜索算法,针对不同版本的SIMON分组密码搜索结果如表3所示。
5 结束语
本文利用SAT/SMT求解器,提出一种全新的自动化搜索分组密码不可能差分和零相关线性闭包的方法。该方法针对分组长度大于64 bit的ARX结构分组密码算法仍然有效。本文应用该方法搜索TEA、XTEA及SIMON分组密码的不可能差分及零相关线性闭包。针对TEA和XTEA,最优不可能差分及零相关线性闭包长度分别为15轮、15轮。本文提出的SIMON32/48/64/96/128的最优不可能差分及零相关线性闭包长度分别为11轮、12轮、13轮、16轮和19轮。
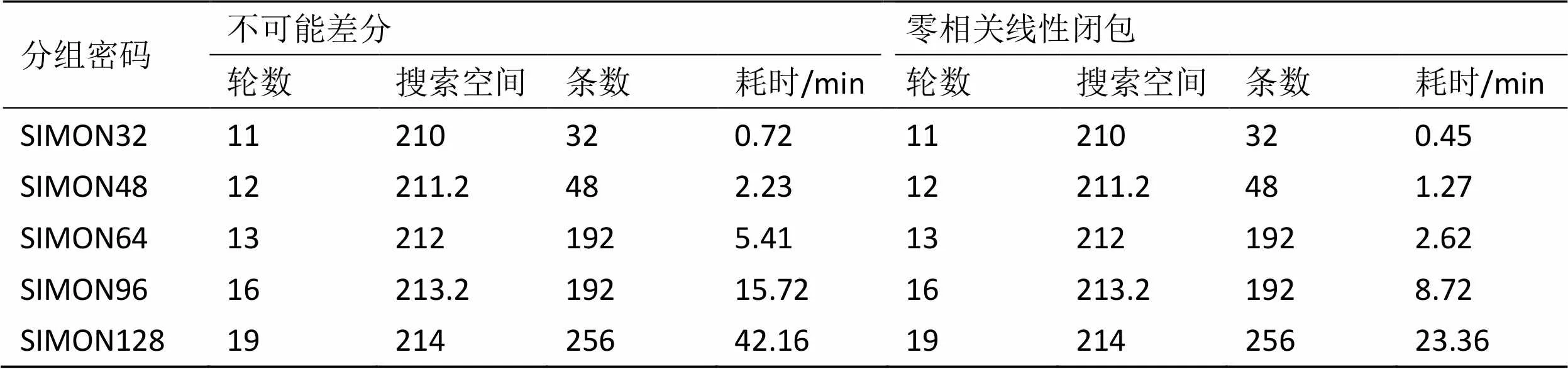
表3 SIMON分组密码搜索结果
[1] KNUDSEN L R. Deal - a 128 bit block cipher[J]. Complexity, 1998.
[2] BIHAM E, BIRYUKOV A, SHAMIR A. Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials[C]//Advances in Cryptology — EUROCRYPT ’99. 1999:12-23.
[3] BIHAM E, BIRYUKOV A, SHAMIR A. Miss in the middle attacks on IDEA and Khufu[C]//The International Workshop on FAST Software Encryption. 1999:124-138.
[4] PHAN C W. Impossible differential cryptanalysis of 7-round advanced encryption standard(AES)[J]. Information Processing Letters, 2004, 91(1):33-38.
[5] LU J, DUNKELMAN O, KELLER N, et al. New impossible differential attacks on AES[C]// Progress in Cryptology-INDOCRYPT. 2008:279-293.
[6] BOURA C, NAYA-PLASENCIA M, SUDER V. Scrutinizing and improving impossible differential attacks: applications to CLEFIA, camellia, lblock and simon[C]//The International Conference on the Theory and Application of Cryptology and Information Security. 2014:179-199.
[7] CHEN J, FUTA Y, MIYAJI A, et al. Improving impossible differential cryptanalysis with concrete investigation of key scheduling algorithm and its application to lblock[C]//The 8th International Conference on Network and System Security. 2014:184-197.
[8] BOGDANOV A, RIJMEN V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers[J]. Designs Codes & Cryptography, 2014, 70(3):369-383.
[9] YI W T, CHEN S Z. Improved integral and zero-correlation linear cryptanalysis of reduced-round CLEFIA block cipher[J]. IACR Cryptology ePrint Archive, 2016:149.
[10] SOLEIMANY H, NYBERG K. Zero-correlation linear cryptanalysis of reduced-round LBlock[J]. Designs Codes & Cryptography, 2014, 73(2):683-698.
[11] XU H, JIA P, HUANG G, et al. Multidimensional zero-correlation linear cryptanalysis on 23-round LBlock-s[M]//Information and Communications Security. Berlin: Springer, 2015.
[12] ZHANG K, GUAN J, HU B, et al. Security evaluation on simeck against zero correlation linear cryptanalysis[J]. IACR Cryptology ePrint Archive, 2015.
[13] KIM J, HONG S, SUNG J, et al. Impossible differential cryptanalysis for block cipher structures[C]//The 4th International Conference on Cryptology. 2003:82-96.
[14] LUO Y, LAI X, WU Z, et al. A unified method for finding impossible differentials of block cipher structures[J]. Information Sciences, 2014, 263(1):211-220.
[15] WU S, WANG M. Automatic search of truncated impossible differentials for word-oriented block ciphers[C]//The International Conference on Cryptology. 2012:283-302.
[16] LIPMAA H, MORIAI S. Efficient algorithms for computing differential properties of addition[C]//The 8th International Workshop on Fast Software Encryption. 2001:336-350.
[17] WALLÉN J. Linear approximations of addition modulo 2n[C]//The 10th International Workshop on Fast Software Encryption (2003). 2003:261-273.
[18] KÖLBL S, LEANDER G, TIESSEN T. Observations on the SIMON block cipher family[C]// Advances in Cryptology - CRYPTO 2015:161-185.
[19] WHEELER D J, NEEDHAM R M. Tea, a tiny encryption algorithm[M]//Fast Software Encryption. Berlin : Springer, 1994:363-366.
[20] BEAULIEU R, SHORS D, SMITH J, et al. The simon and speck families of lightweight block ciphers[J]. IACR Cryptology ePrint Archive, 2013(6): 404.
Automatic method for searching impossible differentials and zero-correlation linear hulls of ARX block ciphers
HAN Ya1,2
(1. The State Key Lab of Information Security, Institute of Information Engineering, Chinese Academy of Science, Beijing 100093, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China)
Firstly, the differences and linear masks propagation equations of ARX ciphers were established. Secondly, the propagation equations were solved by SAT solver and judged valid or not. Finally, differences and linear masks were traversed to search impossible differentials and zero-correlation linear hulls automatically. The proposed algorithm was applied to TEA, XTEA and SIMON family block ciphers. The optimal impossible differentials and zero-correlation linear hulls for TEA, XTEA and SIMON family block ciphers were proposed. Moreover,with DDT and LAT, the algorithm can also be applied to search the impossible differentials and zero-correlation linear hulls of S-box based block ciphers.
impossible differential, zero-correlation linear hull, ARX structure, SAT solver
TP309
A
10.11959/j.issn.2096-109x.2017.00175
韩亚(1989-),男,河南商丘人,中国科学院信息工程研究所博士生,主要研究方向为密码学。
2017-05-10;
2017-06-15。
韩亚,hanya@iie.ac.cn
国家自然科学基金资助项目(No.61379142);国家重点基础研究发展计划(“973”计划)基金资助项目(No.2013CB834203)
The National Natural Science Foundation of China (No. 61379142), The National Basic Research Program of China (973 Program)(No. 2013CB834203)
