基于MATLAB和LINGO的直齿锥齿轮传动优化设计

王沁军，吴志光

（山西机电职业技术学院机械工程系，山西长治046011）

基于MATLAB和LINGO的直齿锥齿轮传动优化设计

王沁军，吴志光

（山西机电职业技术学院机械工程系，山西长治046011）

以大端端面模数met，小锥齿轮齿数z1，锥齿轮宽度b作为设计变量，以锥齿轮总体积最小为优化目标，以齿轮的强度等要求作为约束条件构建出直齿锥齿轮传动优化数学模型。通过实例给出常规设计方案，借助Matlab软件进行连续变量优化求解，利用Lingo软件进行离散变量优化求解，对求解结果进行综合比较，得出优化设计方案。与常规设计相比，锥齿轮总体积下降约32%，优化效果明显，能为设计选型提供参考。

直齿锥齿轮传动；优化设计；连续变量；离散变量

锥齿轮传动应用广泛，强度条件主要为齿面接触强度和齿根弯曲疲劳强度，对于强度校验，按GB /T10062-2003锥齿轮承载能力计算方法进行，其传动常规设计可以按文献[1]和[2]进行。对于其优化设计，文献[3]和[4]采用遗传算法，分别对弧齿锥齿轮传动和可控螺旋角锥齿轮传动进行优化，文献[5]考虑设计变量的离散性，利用枚举法，对直齿锥齿轮传动进行优化，文献[6]采用混合离散复合形法，对弧齿锥齿轮传动进行优化。对于优化设计，主要集中在利用优化求解算法，针对实际问题构建优化数学模型并进行求解。

本文以直齿锥齿轮传动为研究对象，选取大端端面模数met，小锥齿轮齿数z1，锥齿轮齿宽b为设计变量，以两锥齿轮体积之和最小为优化目标，确定了边界和强度约束条件，构建出优化数学模型，利用Matlab进行连续变量优化求解，然后利用Lingo进行离散变量优化求解，综合分析得出优化方案，优化求解结果比初始设计在总体积上得以减小32%，可为设计选型提供必要参考。

1 优化数学模型的建立

1.1 设计变量

通常设计时载荷情况，小锥齿轮传递的转矩T1，齿数比u，小锥齿轮转速n1等均可确定，此时基本设计参数为met，z1，z2，b（或ΦR），∑，δ1，δ2等[1]。其中z2为大锥齿轮齿数，ΦR为齿宽系数，∑为轴线间交角，δ1、δ2分别为小、大齿轮分锥角。如∑已按要求确定，独立的设计变量就只有大端端面模数met，小锥齿轮齿数z1，锥齿轮齿宽b，因此设计变量为：

1.2 目标函数

满足设计条件下，尽量节约材料，以直齿锥齿轮传动中小、大齿轮体积之和最小为优化目标，考虑锥齿轮实际结构的复杂性，较难用准确的关系式表达，故此采用大端与小端分度圆之间的截头圆锥体积进行计算[5]，可表达为：

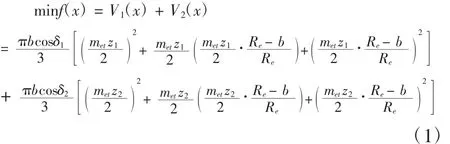
1.3 约束条件

（1）大端端面模数met约束条件

大端端面模数met应符合GB/T12368-1990锥齿轮模数之规定，通常根据设计条件确定范围[4]，取met=2~10，可得：

式中：tanδ1=z1/z2=1/u，tanδ2=z2/z1=1/u，Re为外锥距，按式（2）计算。

（2）小锥齿轮齿数z1约束条件

小齿轮齿数z1通常取16~30之间[1]，可得：

（3）锥齿轮齿宽b约束条件

齿宽b通常取整数，锥齿轮传动的齿宽系数ΦR常取1/4~1/3[1]，可得：

（4）齿面接触疲劳强度条件

根据GB/T10062-2003，应满足齿面接触疲劳强度条件[1-2]，可得：

式中：σH为齿面接触应力（MPa）；σHP为许用齿面接触应力（MPa）；Fmt为齿宽中点分锥上的名义切向力（N）；KA为使用系数；KV为动载系数；KHβ为接触强度齿向载荷分布系数；KHα为接触强度端面载荷分配系数；ZM-B为中点区域系数；ZH为节点区域系数；ZE为弹性系数；ZLS为载荷分担系数；Zβ为螺旋角系数；ZK为锥齿轮系数；dm1为小锥齿轮中点节圆直径（mm）；lbm为中点接触线长度（mm）.根据设计条件，参考国标或文献[1]和[2]，确定以上各参数数值。

（5）齿根弯曲疲劳强度条件

根据GB/T10062-2003，应满足齿根弯曲疲劳强度条件[1-2]，可得：

式中：σF为齿根弯曲应力（MPa）；σFP为许用齿根弯曲应力（MPa）；mmn为中点法向模数；YFa为齿形系数；Ysa为应力修正系数；Yε为重合度系数；YK为弯曲强度锥齿轮系数；YLS为弯曲强度载荷分担系数；KFβ为弯曲强度齿向载荷分布系数；KFα为弯曲强度端面载荷分配系数。根据设计条件，参考国标或文献[1]和[2]，确定以上各参数数值。

2 设计实例与常规设计结果

设计某传动用闭式直齿锥齿轮传动，已知小齿轮传递的转矩为T1=400 N·m，小齿轮转速n1=960 r/min，齿数比u=z2/z1=3，两轮轴线相交成90°，设计精度等级为IT6级，长期工作。大小齿轮均采用20Cr，渗碳、淬火，齿面硬度为58~63 HRC，许用齿面接触应力σHP=1 087 MPa，许用齿根弯曲应力σF=450 MPa[1].

直齿锥齿轮传动的常规设计步骤为[1]：首先，初选小锥齿轮齿数z1，由齿面强度估算公式计算最小小齿轮大端分度圆直径de1.然后确定大端端面模数met和齿轮宽度b，计算其它锥齿轮尺寸参数。最后校核齿面接触疲劳强度和齿根弯曲疲劳强度，如验算合格则设计可行，如不满足条件则需调整参数直到满足强度条件。

根据上述步骤进行设计，可得常规设计结果：大端端面模数met=5.5，小锥齿轮齿数z1=19，大锥齿轮齿数z2=57，外锥距Re=165.229 mm，锥齿轮齿宽b=50 mm，齿宽系数ΦR=0.302 6，小齿轮大端分度圆直径de1=104.5 mm，大齿轮大端分度圆直径de2=313.5 mm，其余参数可由相关公式计算得到。

3 优化求解

3.1连续变量求解

将变量按连续值处理，求解后进行圆整和取标准值得出优化方案[3-4]。对于有约束条件的连续变量优化设计问题，求解方法很多，常规算法有随机方向法、复合形法、可行方向法、惩罚函数法等，还可采用智能算法，如粒子群算法（PSO）、遗传算法（GA）、模拟退火算法（SA）、蚁群算法（ACO）等[7-8]。Matlab软件中，对于非线性约束条件的优化问题，提供了fmincon函数进行求解，而不再需要编写相应的算法程序，使求解更为方便。同时，采用粒子群算法在Matlab软件中进行编程，对该优化问题进行求解，以对比求解结果。

（1）fmincon函数优化求解

根据前述条件，确定各参数的数值或函数关系式，编写优化目标函数文件（aim_1.m）和约束条件文件（const_1.m），以常规设计结果为优化求解初始点，调用fmincon函数进行求解，程序如下：

x0=[5.5 19 50]；

A=[]；b=[]；Aeq=[]；beq=[]；

xlb=[2 16 10]；

xub=[10 30 100]；

options=optimset（'Display'，'iter-detailed'，'MaxFunEvals'，2000）；

[x，fval，exitflag，output]=fmincon（'aim_1'，x0，A，b，Aeq，beq，xlb，

xub，'const_1'，options）

运行程序后可以得到如下求解结果：

X1=[4.5214 21.0216 38.4166]

（2）粒子群算法优化求解

将目标函数和约束条件程序输入到粒子群算法相应程序位置[8]，然后运行粒子群算法程序，可以得到如下求解结果：

X2=[4.5218 21.0240 38.4365]

图1所示为粒子群算法适应度曲线，可以看到初始迭代过程中目标函数下降很快，随着迭代次数的增多，目标函数下降平缓，从91次迭代开始，目标值下降微小，基本不变。比较fmincon函数和PSO算法求解结果，两者相近。根据求解结果，进行取整和取标准值，可得X3=[4.5 21 39]，即大端端面模数met=4.5，小锥齿轮齿数z1=21，齿宽b=39 mm，对于结果的可行性需要校核强度条件。

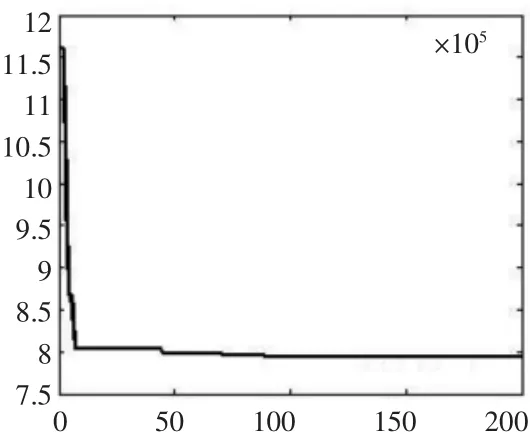
图1 粒子群算法求解适应度曲线

3.2 离散变量求解

由前面分析可知，大端端面模数met、小齿轮齿数z1、锥齿轮宽度b实际都是离散变量，将其作为离散变量进行优化求解，在使用上更为合理和准确。对于离散变量的优化求解，可采用离散化法、离散复合形法、分支定界法等[9-10]，以上方法需要编写相应算法程序即可实现。在Lingo软件中，通过较为简单的程序语言设定即可将变量离散化处理，而目标函数和约束条件的编写与Matlab软件相近，通过设置求解器可较快捷地进行优化求解[11]。

在Lingo软件中编写目标函数和约束条件，通过（x1#EQ#3）#OR#（x1#EQ#3.25）#OR#（x1#EQ#3.5）等语句设定大端端面模数met（x1）为标准值，通过@gin（x2）和@gin（x3）语句设定小齿轮齿数z1（x2）和齿宽b（x3）为整数，然后运行程序进行求解，可得如下求解结果：

X4=[4.52140]

将不同求解结果进行比较，如表1所示，可知由连续变量圆整后的解严格意义上不满足强度约束条件，由于接触应力和弯曲应力与许用值非常接近，在误差范围内是可以应用的。由离散求解方法得到的解，满足强度约束条件，接触应力和弯曲应力略小于许用值。以大端端面模数met=4.5，小锥齿轮齿数z1=21，齿宽b=40 mm作为优化设计结果，优化后的参数比常规设计在锥齿轮总体积上减小约32%，整体优化效果明显。

表1 常规设计与优化设计结果

4 结论

将优化设计理论和方法应用于直齿锥齿轮传动中，以锥齿轮体积之和最小为优化设计目标，分析了边界约束条件和强度约束条件，结合实例得出常规设计方案，通过程序编写构建出优化数学模型。通过fmincon函数和粒子群算法在Matlab软件中进行连续变量求解，分析圆整解可能存在的非可行解等问题，利用Lingo软件将设计变量离散化，进行优化求解，得到优化设计方案，在满足约束条件下优化效果显著。

[1]机械设计手册编委会.机械设计手册：第3卷：第16篇[M]. 3版.北京：机械工业出版社，2004：145-186.

[2]朱孝录.齿轮传动设计手册[M].北京：化学工业出版社，2010：264-316.

[3]黄乾贵，张艳.基于遗传算法的弧齿锥齿轮传动的优化设计[J].机械传动，2003，27（4）：32-33.

[4]李铁军，朱成实，叶龙.基于遗传算法的可控螺旋角锥齿轮传动的优化设计[J].机械传动，2007，31（2）：42-44.

[5]程进.基于枚举法的锥齿轮传动优化设计[J].西昌学院学报（自然科学版），2009，23（1）：44-46.

[6]徐志杨，李艾民，张传辉，等.基于混合离散变量复合形法的弧齿锥齿轮优化设计[J].北京联合大学大学学报（自然科学版），2011，25（3）：34-37.

[7]孙靖民，梁迎春.机械优化设计[M].北京：机械工业出版社，2012：138-165.

[8]高飞.MATLAB智能算法超级学习手册[M].北京：人民邮电出版社，2014：224-416.

[9]陈立周，俞必强.机械优化设计方法[M].北京：冶金工业出版社，2014：217-236.

[10]张幼军，玉荣.行星齿轮减速器的优化设计[J].组合机床与自动化加工技术，2008，（10）：19-22.

[11]谢金星，薛毅.优化建模与LINDO/LINGO软件[M].北京：清华大学出版社，2005：79-131.

The Optimal Design of Straight Bevel Gear Drive based on MATLAB and LINGO

WANG Qin－jun，WU Zhi－guang
（Department of Mechanical Engineering，Shanxi Institute of Mechanical and Electrical Engineering，Changzhi Shanxi 046011，China）

Taking the straight bevel gear drive as the research model，selected the gear's large end module，the tooth number of small bevel gear，and the gear width as design variable，regarded minimal gear volume as optimization goal，the optimal design model is established by setting gear strength and other constraint conditions. Combined with design example，the traditional design scheme is obtained.The optimal solution of continuous variable is obtained through Matlab，and the optimal solution of discrete variable is obtained through Lingo.Then the optimization scheme is obtained by comprehensive analysis of the solutions.Compared with the traditional design scheme，the gear volume is reduced by 32%，so the effect of optimization is significant，can provide the necessary reference for design.

straight bevel gear drive；optimal design；continuous variable；discrete variable

TH132.41

A

1672-545X（2017）06-0030-04

2017-03-09

王沁军（1982-），男，山西晋城人，硕士，研究方向为计算机辅助设计与制造。