基于EFG法圆管环形翅片的传热分析

张丽娜，唐芳，刘吉普，陈优

（1.湖南应用技术学院机电工程学院，湖南常德415100；2.湖南理工职业技术学院太阳能工程学院，湖南湘潭411104）

基于EFG法圆管环形翅片的传热分析

张丽娜1，唐芳2，刘吉普1，陈优1

（1.湖南应用技术学院机电工程学院，湖南常德415100；2.湖南理工职业技术学院太阳能工程学院，湖南湘潭411104）

基于圆管环形翅片的周期性结构特点，建立了圆管环形翅片温的EFG法传热分析模型。通过编程计算，得到了圆管环形翅片的温度、热流量及温度梯度的分布规律。结果表明，EFG法可应用于结构的传热分析，同时，所得结果为圆管的强化传热及散热结构的优化设计奠定了理论基础。

EFG法；环形翅片；传热分析

当前，结构传热的数值分析方法主要有有限差分法、有限元法、有限体积法等。有限差分法主要应用于形状规则的几何体；有限体积法则主要是计算流体动力学中的主要数值方法；有限元法是当前CAE领域中的主流数值方法，克服了有限差分法形状适应能力差的缺点，在数值结构传热分析中得到了广泛应用[1]。然而，有限元法在构造近似函数时，需要借助单元进行插值，在某些情况下网格容易发生畸变，造成计算失败，同时，对于复杂形状的结构，划分高质量的单元仍然是比较困难或者非常费时的工作。

无网格Galerkin（Element-Free Galerkin，EFG）法作为一种非常流行的无网格法，具有计算精度高、收敛快和稳定性好等[2]优点，现已广泛应用于结构大变形[3]、动态裂纹扩展[4]和结构优化[5]等多个领域。

EFG法在构造近似函数时，只需借助一系列离散节点，而无需网格，因此EFG法不存在有限元法所面临的的网格畸变困难，而且EFG法的前处理过程简单，只需利用节点对结构进行离散即可，而无需耗费大量的静力来生成高质量的网格。当前，EFG法在数值传热学中已得到一定的应用[6-7]。本文基于EFG法，建立了圆管环形翅片的温度场分析模型，通过编程计算，得到了环形翅片的温度场分布规律，对圆管的强化传热及其散热结构的优化设计奠定理论基础。

1 热传导问题的EFG离散模型

EFG法利用移动最小二乘法构造位移逼近函数，在二维热传导问题中，其温度场的逼近函数为：

式中准（x）为形函数。若采用罚函数法来处理本质边界条件，对于固体热传导问题，则EFG法的离散形式可表述为：

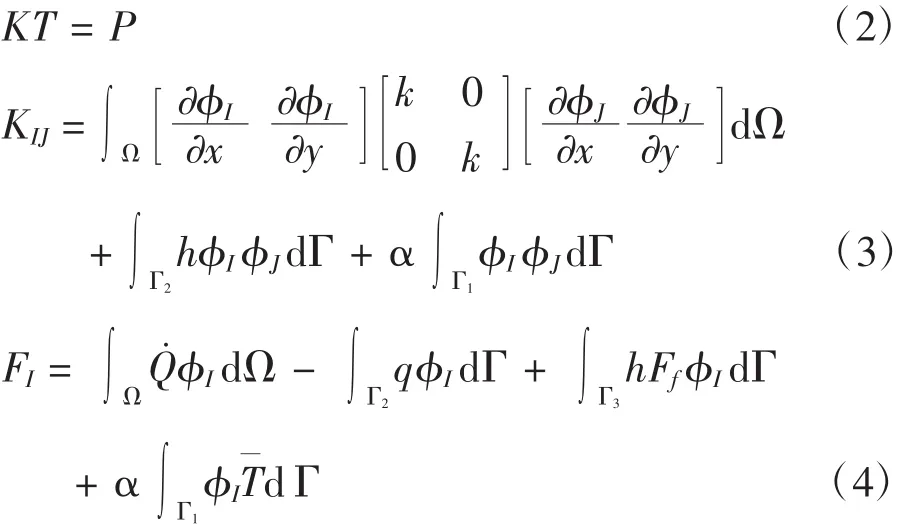
式中，K为总体温度刚度矩阵，由节点对温度刚度矩阵KIJ组装而成；T为节点温度参数向量；P为总体热载荷向量，由节点热载荷向量FI组装而成；α为罚因子。

式（2）与式（3）中均含有积分项，由于EFG法中积分项的被积函数并非简单的多项式函数，因此需要利用高斯积分进行计算。本文基于有限元背景积分网格，采用高斯积分进行计算，如图1所示。

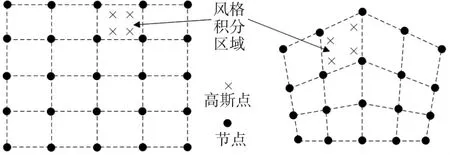
图1 有限元背景积分网格示意图

同时，在本文随后的分析中，采用了线性基函数和三次样条权函数，其节点影响域采用矩形区域。为保证形函数计算的有效性，即要求节点影响域内必须有合适的节点数，本文将节点I的影响域半径dmI取为节点I与距其最近的第m个节点之间的距离Sm.

2 环形翅片的EFG传热分析

2.1 问题描述

图2为圆管外环形翅片的轴对称结构图，其中管内通热流体，管外流体为空气。管道及翅片材料均为不锈钢，热导率为25.96 W/（m·℃）.管内流体的温度为250℃，表面传热系数为249.23 W/（m·℃）；管外流体温度为39℃，表面传热系数为62.3 W/（m·℃）.

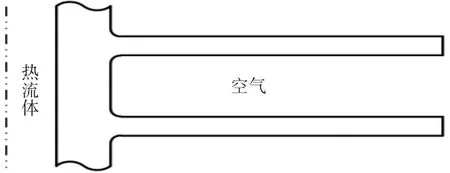
图2 环形翅片几何模型

2.2 分析模型

考虑到圆管环形翅片模型的周期性特点，可截取图3所示的部分结构进行分析，并采用轴对称模型。其边界条件如图3所示，上下边界为绝热条件，其余边界均为对流条件。

图3 环形翅片分析模型

本文采用规则排布的节点进行离散，得到图4所示的节点布置方案，节点总数为1 782.为了计算离散格式中的积分项，需要采用有限元背景积分网格，本文采用与离散节点相重合的有限元背景积分网格，如图5所示，网格总数为1 573.

图4 节点布置

图5 背景积分网格

需注意的是，采用EFG法进行该结构的传热分析时，只需要一系列的离散点来构造温度场的逼近函数，而无需有限元背景网格（仅用于计算离散格式中的积分项，与温度场逼近函数无关），这是EFG等无网格方法与有限元法的本质区别。

2.3 结果讨论

利用EFG传热分析程序，对该环形翅片的分析模型进行求解，并进行后处理，得到了环形翅片的温度场分布云图，如图6所示。由图6可知，最高温度值位于热流体侧，即圆管内壁且距离翅片最远的左上角部位，最低温度值位于翅片的末端。显然，热量是由圆管内部的热流体，经由圆管壁，传递至环形翅片，然后散发至空气中。热流量与温度梯度的分布云图分布如图7、图8所示，由图可知，热流量及温度梯度的最大值均为环形翅片与圆管外壁面连接的过度圆角处。

图6 温度场的分布云图

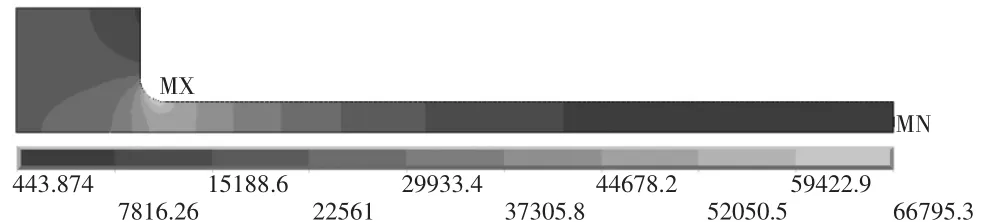
图7 热流量的分布云图

图8 温度梯度的分布云图

3 结论

本文建立了圆管环形翅片的EFG传热分析模型，通过编程计算，得到了环形翅片的温度、热流量及温度梯度的分布规律，结果表明本文方法可行。在作者的下一步工作中，将探讨基于EFG法的结构传热优化，研究工程传热结构的优化设计问题。

参考文献：

[1]王勖成.有限单元法[M].北京：清华大学出版社，2003.

[2]Belytschko T，Lu Y Y，Gu L.Element-free Galerkin meth ods[J].International journal for numerical methods in engi neering，1994，37（2）：229-256.

[3]张希，姚振汉.无网格彼得洛夫伽辽金法在大变形问题中的应用[J].工程力学，2006，23（Sup.I）：16-20.

[4]蔡永昌，朱合华.裂纹扩展过程模拟的无网格MSLS方法[J].工程力学，2010，27（7）：21-26.

[5]龚曙光，曾维栋，张建平.Reissner-Mindlin板壳无网格法的闭锁与灵敏度分析及优化的研究[J].工程力学，2011，28（4）：42-48.

[6]陈民铀，张鹏，彭卉.应用无网格迦辽金法的电力电缆载流量计算[J].中国电机工程学报，2010（22）：85-91.

[7]夏茂辉，赵玉凤，吕鹏，等.改进型无网格迦辽金法在稳定热传导中的应用[J].郑州大学学报工学版，2012，33（6）：71-74.

Heat Transfer Analysis of Annular Fin of Tube based on EFG Method

ZHANG Li-na1，TANG Fang2，LIU Ji-pu1，CHEN You1
（1.School of Electrical and Mechanical Engineering，Hunan Applied Technology University，Changde Hunan 415100，China；2.School of Wind Engineering，Hunan Vocational Institue of Technology，Xiangtan Hunan 411105，China）

In this paper，a heat transfer model of annular fin of tube based on EFG method was established，according to the periodicity of annular fin of tube.The temperature field and temperature gradient of annular fin of tube was obtained by using the EFG program.The result shows that EFG method can apply to heat transfer problem，and it is provided the fundamental for enhancement of heat transfer of tube and optimization design of heat radiation structure.

EFG method；annular fin；heat transfer analysis

TH123

A

1672-545X（2017）06-0016-03

2017-03-14

湖南省教育厅科学研究一般项目（16C1173、16C0745）

张丽娜（1987－），女，河南鹤壁人，硕士，主要从事过程装备仿真及优化和节能与环保等研究；唐芳（1989－），女，湖南永州人，硕士，本科，主要从事数值传热学及太阳能光热利用技术研究。