断续谱线性调频信号特性仿真

徐砚默，张 磊，张 放

(1.南京理工大学，江苏 南京 210094；2.中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)



断续谱线性调频信号特性仿真

徐砚默1，张 磊2，张 放2

(1.南京理工大学，江苏 南京 210094；2.中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

高频雷达工作的恶劣环境促使了对断续谱信号的研究。断续谱信号的频谱随着断续频带大小以及位置变化而变化，影响了断续谱信号的模糊函数。推导了断续谱线性调频信号的模糊函数，讨论了频带断续大小以及位置变化对距离模糊函数的影响，针对脉压后旁瓣较高的问题，采用失配滤波的方法进行旁瓣抑制，利用迭代最小二乘法对失配滤波器的系数求解。

断续谱；模糊函数；失配滤波；距离旁瓣

0 引 言

高频超视距雷达工作在3～30 MHz的频段内，在此频段内存在着大量的干扰，主要由短波通信干扰、天电干扰、电磁对抗干扰等[1]。应用传统的连续谱信号时会受到外部的干扰，在后期信号处理时需要考虑各种干扰。英国学者S. D. Green总结了高频雷达的波形设计，提出了断续谱信号的概念，根据实时频谱检测的结果，对接收信号进行截断，得到的信号频谱是断续的，通过频谱重构的方法进行处理[2]。从波形设计的角度，可以根据实时频谱检测结果，在发射端主动避开这些干扰的频段，通过合成几段不连续的频带来满足系统带宽的要求。按信号的调制方式,断续谱信号可以分为断续谱线性调频信号、断续谱频率编码信号、断续谱调频断续波和断续谱正交频分复用(OFDM)信号。本文主要研究断续谱线性调频信号。

1 断续谱线性调频信号

1.1 断续谱线性调频信号的信号形式

断续谱线性调频信号又被称为分段线性调频信号[3]。从信号的频谱来看，断续谱线性调频信号的频谱由I段频谱组成，各段频谱之间是不连续的，但是每段频谱内是连续的线性调频信号，每个子频段内信号的调频频率斜率都为K，各段信号的基带信号相位是连续的。从信号的时域波形来看，断续谱线性调频信号在每个信号周期内是连续的。图1为断续谱线性调频信号频率和时间的关系示意图。

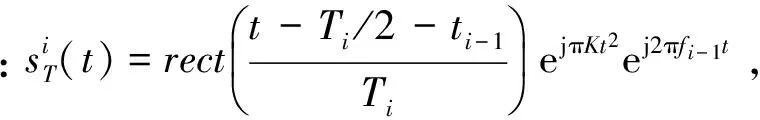
(1)

第i段信号的调频带宽Bi=K(ti-ti-1)，所有分段频谱宽度的总和记作占有带宽Ba:

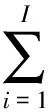
(2)

可以看出断续谱线性调频信号的总带宽只和信号的调频斜率K以及信号的时间跨度有关。记断续谱的最高频率和最低频率的差为调频跨度Bs:

Bs=fI-1-f0+K(tI-tI-1)

(3)

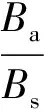
1.2 断续谱线性调频信号的零多普勒模糊图

对于雷达信号波形u(t)，定义其模糊函数为[1]：

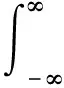
(4)

式中：τ为时间延时；ξ为多普勒频率。

(5)

令p=t-ti-1，代入上式得到：

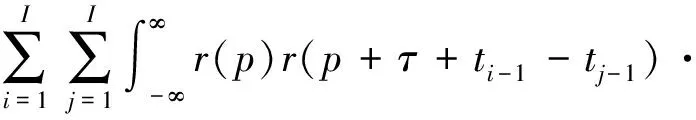
(6)

当i=j时，模糊函数为中心模糊带：

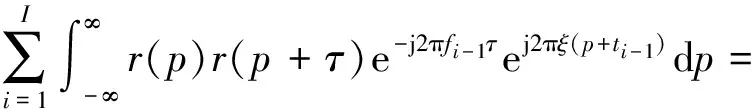
(7)

(8)

式中：χr(τ,ξ)为r(t)的模糊函数。

断续谱线性调频信号的表达式为：

sT(t)=u(t)ejπKt2

(9)

根据模糊函数的性质(时域平方相位的响应)可以得到：

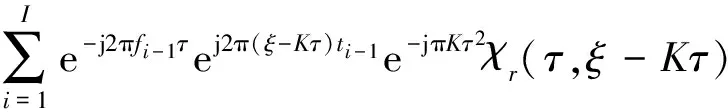
(10)

由式(10)可以看出:信号的调频斜率K、每段信号的初始频率fi-1、信号的分段数I、每段信号的持续时间Ti综合影响着信号的模糊函数。

仿真参数：信号的占有带宽40 kHz，时宽12 ms，分段数I=3，每段的起始频率分别为-30 kHz、-10 kHz、20 kHz，每段的终止频率为-20 kHz、10 kHz、30 kHz。信号的频谱和零多普勒模糊图见图2。

2 频谱断续对信号脉压后旁瓣的影响

2.1 频带断续的大小对信号脉压后旁瓣的影响

根据式(10)得到：

(11)

讨论零多普勒的情况，所以令ξ=0，则：

(12)

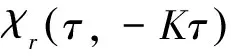
当断续频带的位置固定时，断续频带大小的变化体现为各个连续频段的起始频率的变化。仿真参数：信号的占有带宽为40 kHz，时宽为12 ms，设定一个断续的频带，将断续频带的位置固定在频带的中间，改变断续频带，从0 kHz到35 kHz，分为100个等间隔依次变化，相应的信号频谱占有率从100%变化到46.67%，信号经过脉压后的最大旁瓣随频带断续大小变化图如图3所示。

从图3中曲线可以看出：断续频带大小和最大旁瓣的关系是非线性的。随着断续频带带宽的逐渐变大，相应的频谱占有程度逐渐减小，信号脉压之后的最大旁瓣值逐渐变大。断续频带带宽越大，可以相关的信息越少，导致旁瓣值变大。当断续频带大小为0时，断续谱信号变为连续谱信号，脉压后的最大旁瓣为-13.2 dB。当断续频带大小为15 kHz时(对应的频谱占有率为72%)，此时的最大旁瓣为-4.5 dB，这么高的旁瓣对后续信号处理带来了很大的难度。

2.2 频带断续的位置对信号脉压后旁瓣的影响

当频带断续的大小固定时，断续频带位置的变化体现在式(7)中矩形脉冲函数的模糊函数χr(τ,-Kτ)的变化和中间起始频率大小的变化，这种情况是比较复杂的。

仿真参数：信号的占有带宽为40 kHz，时宽为12 ms，设定一个断续的频带，信号起始频率分别为-22.5 kHz、18.5 kHz，终止频率分别为13.5 kHz、22.5 kHz，断续频带的大小为5 kHz，相应的频谱占有程度为88.89%。固定断续频带的大小，将断续频带的中心位置从整个频带的中心位置变化到整个频带的边缘位置。图4为信号脉压后的最大旁瓣随断续频带位置变化图，横坐标为断续频带的中心位置和占有带宽之比。

从图4中可以看出：断续频带位置变化和最大旁瓣的关系是非线性的。当断续频带位置处于整个频带中心时，信号脉压后的最大旁瓣是最大的，随着断续频带中心位置偏离频带中心，最大旁瓣逐渐变小。当断续频带处于整个频带的边缘时，断续谱线性调频信号变成了连续谱线性调频信号，脉压后的旁瓣为-13.2 dB。从图4中可以看出，存在着使得最大旁瓣最小的位置。在条件允许的情况下，应该尽量选择断续频带中心靠近整个频带边缘的位置。

3 断续谱线性调频的信号处理

3.1 信号处理流程

由于断续谱线性调频信号的频谱不连续，相应的频率发生了跳变，直接进行匹配滤波时就会出现旁瓣较高的问题，可采用失配滤波的方法对信号进行处理[4]。发射信号是已知的，根据发射信号求得信号的距离模糊函数，事先求得旁瓣抑制时的滤波器系数。将接收信号和发射信号进行相关处理，对得出的结果再进行失配滤波，降低距离旁瓣。整个处理过程框图如图5所示。

可以通过最小二乘法求解滤波器的系数。为了得到较好的效果，本文采用了迭代最小二乘法进行滤波器系数的求解。

3.2 失配滤波对距离旁瓣的抑制

失配滤波抑制距离旁瓣是基于对信号的距离模糊函数旁瓣的抑制，设信号自相关函数序列为s=[s0,s1,s2,…,sN-1]，那么构造的信号矩阵为：

(13)

失配加权的系数为x，期望输出为d，那么矩阵方程为Ax=d，其中A是(2N-1)×N的矩阵，x是待求的N维列向量，d是(2N-1)维列向量，在期望处的值为1，其余地方都为0，即为：d=[0,0,…,0,1,0,…,0,0]T,将迭代加权系数矩阵R进行初始化如下：

(14)

迭代过程中，R按照以下的形式进行变化：

失配加权系数为：

(15)

迭代的终止条件如下所示:

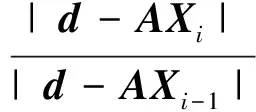
(16)

仿真中的断续谱线性调频信号一共有4段，基带信号的初始频率分别为-8 kHz、-1 kHz、5 kHz、15 kHz，终止频率分别为-3 kHz、1 kHz、8 kHz、20 kHz，那么信号的总占有带宽为15 kHz，信号的时宽为10 ms，相应的频谱占有率为53.5%。

进行失配滤波处理前的距离模糊函数如图6所示。

从图6中可以看到：未经失配处理的信号距离模糊函数的旁瓣已经高达-8.796 dB。

经过迭代最小二乘法失配处理后的距离模糊函数如图7所示。

从图7中可以看出：经过迭代最小二乘法求解滤波系数，利用求得的系数失配滤波处理后信号距离模糊函数的旁瓣得到了降低，为-28.6 dB，可以通过调整设定的门限进一步迭代，使得旁瓣进一步降低。

4 结束语

本文首先给出了断续谱线性调频信号的表达形式，对这种信号的模糊函数进行了理论上的推导，然后通过仿真分析了频带断续的大小和频带断续的位置对信号脉压后旁瓣的影响，接着给出了信号处理的流程图，采用失配滤波进行旁瓣的抑制，通过迭代最小二乘法求解失配滤波器的系数，通过仿真比较了进行失配滤波和未进行失配滤波断续谱信号的距离旁瓣，发现失配滤波是降低断续谱信号距离旁瓣的有效方法。

[1] 丁鹭飞,耿富录,陈建春.雷达原理[M].北京：电子工业出版社,2014.

[2] 位寅生,刘永坦.随机断续高频雷达波形设计和处理[J].电子学报,2002(3):437-440.

[3] 王勤,万显荣,杨子杰,等.基于CLEAN算法的非连续谱线性调频中断波信号处理[J].电波科学学报,2009,24(2):243-247.

[4] 熊俊志,杨子杰,王勤.基于内插/外推的非连续谱高频雷达二维处理[J].电波科学学报，2006(5):735-739.

CharacteristicSimulationofLinearFrequencyModulationSignalwithDiscontinuousSpectrum

XU Yan-mo1,ZHANG Lei2,ZHANG Fang2
(1.Nanjing University of Science and Technology,Nanjing 210094,China; 2.The 723 Institute of CSIC,Yangzhou 225001,China)

The bad environment of high frequency radar promotes the research into discontinuous spectrum signal.The spectrum of discontinuous spectrum signal changes with the size and position of intermittent frequency band,which influences the ambiguity function of discontinuous spectrum signal.This paper deduces the ambiguity function of linear frequency modulation signal with discontinuous spectrum,discusses the influence of frequency band discontinuous size and position change on the range ambiguity function,aiming at the problem that the side lobe after pulse compression is relatively high,adopts the mismatched filtering method to perform side lobe suppression,uses the iterative least square method to solve the coefficients of mismatched filter.

discontinuous spectrum;ambiguity function;mismatched filtering;range side lobe

2017-03-01

TN957.51

：A

：CN32-1413(2017)03-0045-04

10.16426/j.cnki.jcdzdk.2017.03.011