多模圆阵干涉仪校正方法研究
2017-07-31杨跃轮王书楠王诗臻
杨跃轮,王书楠,王诗臻
(1.海军驻上海地区电子设备军事代表室,上海 201800;2.上海微波设备研究所,上海 201802;3.郑州成功财经学院,河南 郑州 451200)
多模圆阵干涉仪校正方法研究
杨跃轮1,王书楠2,王诗臻3
(1.海军驻上海地区电子设备军事代表室,上海 201800;2.上海微波设备研究所,上海 201802;3.郑州成功财经学院,河南 郑州 451200)
研究了前端通道幅度和相位不一致性对多模圆阵干涉仪性能的影响,不一致性会使矩阵网络的各个输出模式产生非线性叠加,从而使矩阵输出的相位误差与不一致性呈现非线性关系,介绍了前端幅相一致性的参考指标,提出了一种在矩阵后端校正前端通道不一致性的实时校正算法,并对校正的性能进行了分析。
圆阵干涉仪;相模理论;巴特勒矩阵;通道不一致性;校正方法
0 引 言
作为无源测向系统,圆阵干涉仪具备方位宽开、频率宽开、体积小、测向精度高等优点[1-3]。但是由于巴特勒矩阵的插损较大,造成这种系统很难获得高灵敏度,严重影响了这种系统的应用前景。如果能够在巴特勒矩阵的前端通道内增加低噪声放大器,可以有效改善系统灵敏度,大大提高系统性能。但是在以往的研制过程中,发现在前端通道内增加低噪放后,会使模式输出端的相位产生严重误差,这种误差与前端低噪放的相位不一致性不成比例。在前端通道幅度不一致性小于±3 dB、相位不一致性小于±15°的情况下,通过矩阵输出得到的相位误差曲线最大起伏超过110°(未加放大器时只有14°~45°)。如图1、图2、图3所示。为了解决这一问题,本文尝试分析前端通道不一致性对系统输出的影响,给出前端通道一致性的参考指标,最后还将提出一种校正算法。
1 相模理论与圆阵干涉仪
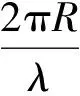
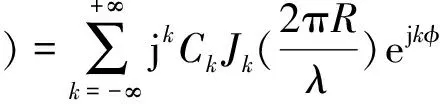
(1)
如果电源阵的激励函数满足特定分布,使得其傅里叶级数只在k阶时不为零,圆阵便可以得到单一的k阶相模方向图,其表达式为:
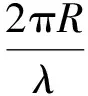
(2)
反之亦然,此时根据来波信号经过圆阵系统后的相位响应,就可以以k倍的精度判断其来波方位。圆阵干涉仪正是利用这个原理工作的。
离散圆阵可以看做是对连续圆阵的取样,其方向图可以表达为如下形式:
E(θ,φ)=
(3)
式中:N为天线单元的个数;Vi为第i个天线受到的激励;Fa(θ,φ)为天线单元方向图;λ为天线的工作波长;R为圆阵半径;θ、φ为以圆阵中心为原点的极坐标系的离轴角和方位角;φi为第i个天线所在的方位角。
图4取天线单元为方位面上的全向天线。则式(3)简化为:

(4)
对长度为N的激励序列V作傅里叶级数展开,可以得到:
(5)
对于k阶相模,取激励序列满足:

(6)
取Sk=1,代入式(4),利用狄拉克函数的性质和贝塞尔函数的积分表达形式,最终可以得到离散圆阵下k阶相模的方向图:
Ek(θ,φ)=
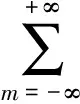
(7)
对比式(7)和式(2)可以发现,在离散圆阵中,k阶相模的方向图不再是单一的幅度相位模式,而是由基波和无数高次谐波叠加而成。虽然每一次谐波的幅度都是水平全向,其相位以一定斜率线性变化;但是其叠加之后,幅度将发生起伏,相位也将发生抖动。其幅度和相位曲线如图5所示。

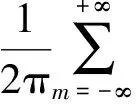
(8)
(9)
式中:Dp(θ)为对天线单元方向图作傅里叶级数展开后的系数。

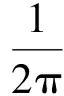
(10)
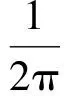
(11)
此时k阶相模相位曲线的斜率与N∓k阶相模的相位曲线斜率相同,只是方向相反。高阶的相位斜率通常是无法稳定存在的,只有经过特定设计的圆阵在较窄的带宽内才可以获得高阶的相位斜率。

对式(6)进一步处理,将k阶相模的强制相位关系提出,并写成矩阵形式:
V=S·Bu
(12)
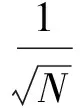
当M=N时,巴特勒矩阵为满秩矩阵。由于高阶相模不可用,为了节省设备量,通常取M (13) (14) (15) 将式(14)代入式(13)得: (16) (17) 将其带入式(16),并令各阶相模的外加激励相等,于是得到: (18) 图6(a)、(b)给出了单元为全向天线的八元圆阵,在前端通道最大幅度不一致性≤±3 dB、相位不一致性≤±15°时,从-2阶相模到+2阶相模的幅度和相位方向图。图6(c)给出了各模式相位方向图相对于理想相位方向图的相位误差曲线。其中实线为存在不一致性影响的圆阵响应。虚线为没有不一致性影响的圆阵响应。从图中可以看出,前端通道的不一致性使幅度起伏增大到10 dB左右,相位误差增大到接近50°。而相位误差曲线的相对起伏达到70°。而不存在前端通道不一致性影响时,相位误差曲线的起伏仅在最大4°左右,幅度方向图的起伏小于3 dB。 当天线单元方向图为指向性天线时,圆阵受不一致性的影响可能会减小。实际上,天线单元方向图有较大的前后比或者单元间较好的隔离度都会改善不一致性对圆阵的影响。此外天线单元间的相对间距对此也有影响。为了定量说明问题,本文针对方向图满足余弦函数的天线单元组成的八元圆阵,在6 GHz频点内进行计算,以便为提出前端通道幅相不一致性的指标上限提供参考。图7(a)为天线单元方向图。 在给定最大幅度不一致性和最大相位不一致性的前提下,随机产生100组随机数来扰动前端通道,然后记录所有100次计算中误差曲线最大起伏的均方根作为平均最大相位误差。据此画出平均最大相位误差随最大幅度不一致性和最大相位不一致性的变化曲线。 图7(b)~(f)分别为-2~2模时,平均最大相位误差在最大幅度不一致性分别为±0.5 dB、±1 dB、±2 dB、±3 dB时随最大相位不一致性的变化曲线。 从图7中可以看出,平均最大相位误差对前端通道幅度不一致性的影响也相当敏感,而幅度一致性相对于相位一致性更容易校准。如果要求相位误差曲线的相对起伏小于45°,则需要前端通道的幅度不一致性小于±2 dB、相位不一致性小于±10°。应当注意的是,这一指标要求也包含天线和矩阵本身产生的不一致性在内。 从图2中可知,由于放大器的幅频曲线和相频曲线是随频率抖动的,电缆或其它无源校正装置无法得到与之相匹配的曲线进行校正。此外,无源的校正方法无法对其进行实时校正。 本文提出一种校正算法,在矩阵后端对前端通道不一致性进行实时校正。其基本思路是利用1个外加的校正源经过1个模拟理想巴特勒矩阵k阶模式输出的线性移相网络(由8个四位数控移相器组成),通过开关向前端通道中灌入校准信号。校准信号被接收机接收后,把得到的幅度和相位结果送入现场可编程门阵列(FPGA)以计算所需的复校正系数。测向时,对于k阶模式,接收机把各阶模式的结果乘以校正系数相加,便得到校正后的结果。系统框图如图8所示。 p=1,…,M (19) p=1,…,M (20) B是一个M×M的矩阵,对其求逆得到: C=B-1 (21) (22) 本文校准方法的思路是对巴特勒矩阵模式端口的直接输出加权相加,以抵消前端通道不一致性产生的附加相模的影响。对于满秩的巴特勒阵(M=N),任意附加相模的影响都可以通过相应阶模式端口的输出加以抵消。但是对于不满秩的巴特勒矩阵(M 分别针对由8×8巴特勒矩阵馈电的八元圆阵和由8×5巴特勒矩阵馈电的八元圆阵进行了仿真。仿真结果在图9、图10中给出。在仿真中,对前端通道的最大幅度不一致性和最大相位不一致性分别设定为±3 dB和±20°。圆阵周长与单元个数之比为0.4,天线单元为全向天线。图中实线代表没有不一致性影响时系统的输出,虚线代表前端通道存在不一致性时的输出,点画线代表经过校正后系统的输出。 图9是8×8巴特勒矩阵馈电的圆阵方向图,以及其相对于理想相位曲线的误差。从图中看出,经过校正后圆阵的响应与没有通道不一致性影响时的响应几乎完全重合,相位曲线的起伏与理论上的起伏一致。这证明,在满秩巴特勒矩阵馈电时,这种校正算法在理想情况下能够完全校掉前端通道幅相不一致性的影响。 为了更全面地考察本文提出的校正方法在巴特勒矩阵不满秩时的校正结果,进一步用蒙特卡洛法进行仿真验证。在图11中,前端通道的幅相不一致性为随机产生,其幅度和相位最大不一致性不超过前文设定。计算校正前后各阶模式相位误差曲线的最大起伏值,并在各阶模式之间取平均。随机产生的次数为100次,每次的数据记录下来并绘成曲线。图中虚线为校正前的结果,实线为校正后的结果。从中可以看出,校正后误差曲线起伏平均为15°~20°,校正前则为25°~50°,校正后比校正前要小10°~40°。可见校正效果还是比较明显的。 当圆阵干涉仪的前端通道存在有源器件时,将引入较大的幅度相位不一致性,根据相模理论,这种不一致性将在原有的相位模式响应中引入其它各阶相模,从而产生非线性的幅度和相位误差。这种误差在不一致性不太大的情况下,也可能会大到难以忍受的程度。单纯依靠在前端通道中进行相位补偿不易消除这种误差。 本文通过仿真分析了相位误差随不一致性变化的曲线,提出了对前端幅度和相位不一致性进行约束的参考指标,最后还提出一种校正算法,在矩阵后端对前端通道不一致性进行校正。仿真表明,对于满秩巴特勒阵馈电的圆阵干涉仪,这种算法可以准确校正前端通道不一致性带来的误差。对于不满秩巴特勒矩阵馈电的圆阵干涉仪,这种方法也可以有效改善前端不一致性的影响。 [1] SHELEG B.A Matrix-fed circular array for continuous scanning[J].Proceedings of The IEEE,1968,56(11):2016-2027. [2] MURPHY S,EYRING P M.2~18 GHz Circular amy interferometer DF antenna system[C]//IEEE Antenna and Propagation Society International Sympisium 1998 Digest.Atlanta,GA,USA:IEEE Press,1998:2332- 2335. [3] 陈俊华.圆阵干涉仪测向技术技术总结报告[R].国防技术报告,2006. [4] ISHLMARU A.Theory of unequally-spaced arrays[J].IRE Transactions on Antennas and Propagation,1962,10(6):691-702. [5] JOSEFSSON L,PERSSON P.Conformal Array Antenna Theory and Design[M].Hoboken,New Jersey:John Wiley & Sons,Inc.,2006. [6] HANSEN R C.Phased Array Antenna[M].Hoboken,New Jersey:John Wiley & Sons,Inc.,Wiley,1998. [7] 王书楠,王诗臻,谭小花.多模圆阵干涉仪的误差分析[C]//全国天线年会.北京:电子工业出版社,2013. ResearchintoTheCorrectingMethodforMulti-modeCircularArrayInterferometer YANG Yue-lun1,WANG Shu-nan2,WANG Shi-zhen3 This paper studies the influence of amplitude and phase inconsistency in front-end channels on multi-mode circular array interferometer performance,and the inconsistency will make each output mode of matrix network to generate nonlinear superposition,thereby make the phase error of matrix outputs and inconsistency present nonlinear relationship,introduces the reference indexes of front-end amplitude and phase consistency,puts forward a real-time correcting algorithm on the rear-end of matrix to correct the amplitude and phase inconsistency in front-end channels,and analyzes the correcting performance. circular array interferometer;phase mode theory;Butler matrix;channel inconsistency;correcting method 2017-03-31 TN971.1 :A :CN32-1413(2017)03-0005-07 10.16426/j.cnki.jcdzdk.2017.03.002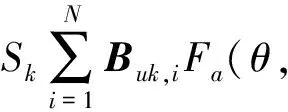
2 前端通道不一致性的影响

3 校正算法研究


4 校正效果分析
5 结束语
(1.Naval Military Representative Office of Electronic Equipment in Shanghai Area,Shanghai 201800,China; 2.Shanghai Research Institute of Microwave Equipment,Shanghai 201802,China;3.Zhengzhou Chenggong University of Finance and Economics,Zhengzhou 451200,China)
