利用单纯形—粒子群算法识别二维河流水质参数
2017-07-29袁帆刘元会郭建青
袁帆+刘元会+郭建青
摘要:将单纯形-粒子群混合算法应用于分析二维河流横向扩散情况下的水团示踪试验数据,估计河流的横向扩散系数、断面平均流速和污水排放位置。数值试验结果表明:(1)加速因子c1,c2和参数初值取值范围综合影响粒子的搜索能力,当加速因子c1=c2=1.72时,有利于保持粒子的搜索能力;(2)在同样的条件下,混合算法的时间性能指标值小于单一的粒子群优化算法;(3)参数初值的取值范围对混合算法收敛性几乎没有影响;(4)混合算法可以有效地应用于河流水质数学模型参数识别问题。混合算法能改善粒子群算法在迭代后期出现的收敛速度慢、早熟的不足,是分析河流水质模型参数的一种有效方法。
关键词:河流水质模型;单纯形算法;粒子群算法;混合算法;时间性能指标
中图分类号:TV211.1 文献标志码:A 文章编号:1672-1683(2017)04-0193-05
Abstract:Simplex-particle swarm hybrid algorithm (SM-PSO)was applied to analyze the experimental data of water quality of river in two-dimensional transverse dispersion,and to estimate the transverse dispersion coefficient,mean velocity of river,and location of continuous pollutant discharge.The results of numerical experiment show that:(1)SM-PSO algorithm can be effectively employed to analyze the experimental data of water quality and estimate water quality parameters.(2)Under the same condition,the time performance indicator of SM-PSO is less than that of PSO algorithm.(3)The range of initial guess value of water quality parameters has little influence on the convergence speed .(4)c1,c2 and the range of initial guess value have synthetic influences on the search capability in operation.When c1=c2=1.72,the search capability can be kept properly.SM-PSO algorithm can overcome the problem of PSO algorithm where it easily drops into local convergence and premature convergence.The hybrid algorithm was proved to be an effective way to estimate parameters for river water quality models.
Key words:water quality model of river;simplex algorithm;particle swarm algorithm;hybrid algorithm;time performance indicator
河流水質参数可以反映河流水体的物理、化学和生物动力学过程,是建立河流水质数学模型、进行河流水质预报和对河流水质状态进行有效控制的基本参数。获得水质参数的主要途径有:经验公式法、理论公式法和示踪试验法。前两者由于移植性差、误差大、耗费的人力和财力巨大,因而国内外许多学者一般采用示踪试验法进行水质参数估计。针对一维河流水团示踪试验的数据分析方法有:单站法、双站法、演算法[1]、直线图解法、相关系数极值法[2]、随机搜索算法[3]、模糊线性回归法[4]、改进的人工鱼群算法[5]、差分-单纯形法[6]等。然而,实际中河床较为不规则,应用一维河流水团示踪试验进行参数估计会导致较大的误差。目前有关二维河流水团示踪试验,确定河流横向扩散系数的方法较少,主要有矩法[7]、直线图解法、相关系数极值法[8]等,这些方法在实际求解中都有一定的局限性[9]。智能优化算法的出现,为解决二维河流水质参数问题提供了很大的方便。例如:模拟退火算法[10]、粒子群优化算法、人工神经网络算法[11]、混沌粒子群算法[12]、人工根系算法[13]等都被用来进行水文参数识别。
粒子群优化算法(Particle Swarm Optimization,PSO)[14-15]最早是由Eberhart和Kennedy 基于群鸟觅食提出的,适用于求解不可微、非线性和多峰值的复杂优化问题,是一种基于迭代的群体寻优算法。算法可以同时利用个体局部信息和群体全局信息指导搜索,收敛速度快。但是,该算法存在早熟收敛现象和在迭代后期易出现震荡的缺点,不能绝对保证搜索到全局最优解。针对这些问题,国内外许多学者又做了大量工作,提出了许多的改进算法[16-19];单纯形法(Simplex Method,SM)[20]做为一种不用计算梯度,只需计算凸多边形顶点适应度值的局部寻优算法,具有局部搜索能力强,计算量小的优点。为了改进粒子群优化算法的性能,本文将单纯形算法引入到粒子群优化算法中,构造了单纯形-粒子群混合算法(SM-PSO),对算法参数进行扰动分析,观察其收敛性的变化,进而确定合理的算法参数,然后对比分析单一的PSO算法和SM-PSO混合算法的时间性能指标和收敛率。
1 单纯形-粒子群混合算法
1.1 单纯形和粒子群优化算法简介
单纯形算法也可称为可变多面体搜索法,是一种通过当前数据来确定搜索方向的局部搜索方法。其基本原理是:在n维欧氏空间中,构造一个包含n+1个顶点的凸多面体,求出每一个顶点的适应度值,并确定其中的最优点、次优点和最差点,然后利用反射、延伸、压缩等策略找到一个较好点,将最差点取代,构成新的多面体。这样重复迭代直到找到或逼近一个最优点。
3.2 算法参数初值取值范围和加速因子对收敛性的影响
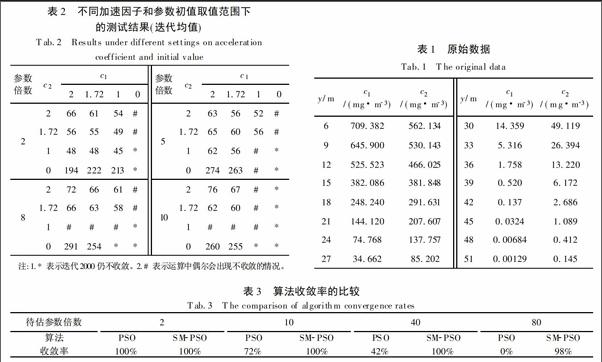
加速因子c1,c2决定了粒子寻优过程中本身经验信息和其他粒子的经验信息对粒子运动轨迹的影响。较大的c1值,会使粒子较多的在局部徘徊,而较大的c2值,会使粒子过早收敛到局部最优值,本文在此原理的基础上设计了使两个加速因子根据迭代次数线性递减的方案,但是得出的结果却不如使两个因子固定的方法好,从而对加速因子取何值时算法的收敛性最佳,且参数取值范围对加速因子的取值有何影响进行分析。取种群规模N=50,二维河流水团示踪试验参数初始取值范围分别是其真值的2、5、8和10倍,对SM-PSO算法中学习因子的不同取值进行100次试算并计算迭代次数的平均值,结果见表2。
文中算例给定的最大迭代次数Imax,分别对PSO算法和SM-PSO算法进行100次试算,两种算法的平均迭代次数分别为158和60次,算法一步迭代的平均计算时间分别为17.02 s和8.84 s,则算法的性能指标值为ESM-PSO=0.265 2,EPSO=1.344 6。SM-PSO算法的时间性能指标值小于PSO算法的时间性能指标值,说明混合算法较单一的PSO算法在收敛速度上有很大的提升。
5 结语
本文构建的单纯形-粒子群优化算法能够有效地应用于河流水质参数优化问题,数值试验结果表明:(1)SM-PSO算法程序简单、计算精度高、收敛速度快;(2)参数初值取值范围对加速因子取值较为明显,文中建议取值为c1=c2=1.72;(3)SM-PSO算法较单一的PSO算法有更好的收敛率,在时间性能指标上也优于PSO算法。总之,SM-PSO混合算法较其他方法寻优能力更强,是分析河流水质模型参数的有效算法之一。
参考文献(References):
[1] 余常昭.环境流体力学导论[M].北京.清华大学出版社1992:180-181.(YU Chang-zhao.Introduction to environmental fluid dynamics[M].Beijing:Tsinghua Press,1992:180-181.(in Chinese))
[2] 郭建青,王洪胜,李云峰.确定河流纵向离散系数的相关系数极值法[J].水科学进展,2000,11(4):387-391.(GUO Jian-qing,WANG Hong-sheng,LI Yun-feng.The correlation coefficient extreme value method to determine the dispersion parameters of river[J].Advances in Water Science,2000,11(4):387-391.(in Chinese))
[3] 郭建青,周宏飞,李彦等.随机搜索算法在确定河流水质参数中的应用[J].水文,2010,30(2):25-28.(GUO Jian-qing,ZHOU Hong-fei,LI Yan,et al.Chaotic optimization for parameter estimation of water quality of river[J].Journal of China Hydrology,2010,30(2):25-28.(in Chinese))
[4] 康瑞龙,常安定,郭建青.一维河流水团示踪试验数据的模糊线性回归[J].水利水电科技进展,2012,32(4):19-22.(KANG Rui-long,CHANG An-ding,GUO Jian-qing.A fuzzy linear regression model for tracer test data of one-dimensional rivers[J].Advances in Science and Technology of Water Resources,2012,32(4):19-22.(in Chinese))
[5] 陈广洲,徐晓春,王家权等.改进的人工鱼群算法在水质识别中的应用[J].水力发电学报,2010,29(4):108-113.(CHEN Guang-zhou,XU Xiao-chun,WANG Jia-quan,et al.Application of a modified artificial fish swarm algorithm to identification of water quality parameters[J].Journal of Hydroelectric Engineering,2010,29(4):108-113.(in Chinese))
[6] 劉元会,付翠,郭建青等.识别河流水质参数的单纯形-差分进化混合算法[J].水利发电学报,2015,34(1):115-120.(LIU Yuan-hui,FU Cui,GUO Jian-qing,et al.Simplex-differential evolution hybrid algorithm for parameter identification of river water quality model[J].Journal of Hydroelectric Engineering,2015,34(1),115-120.(in Chinese))
[7] 金士博,杨汝均.水环境数学模型[M].北京:中国建筑工业出版社,1987.(JIN Shi-bo,YANG Ru-jun.Mathematical model of water environment[M].Beijing:China Architecture & Building Press,1987.(in Chinese))
[8] 郭建青,李彥,王洪胜等.分析二维河流水质试验数据的相关系数极值法[J].水力发电学报,2010,29(4):103-106.(GUO Jian-qing,LI Yan,WANG Hong-sheng,et al.Correlation coefficient extreme method for analyzing the 2-D data of water quality experiment of river stream[J].Journal of Hydroelectric Engineering,2010,29(4):103-106.(in Chinese))
[9] 顾莉,华祖林.天然河流纵向离散系数确定方法研究的进展[J].水利水电科技进展.2007,27(2):85-89.(GU Li,HUA Zu-lin.Advances in determination of longitudinal dispersion coefficient of natural rivers[J].Advances in Science and Technology of Water Resources,2007,27(2):85-89.(in Chinese))
[10] 郑红星,李丽娟.水质模型参数的非数值随机优化[J].地理研究,2001,20(1):97-102.(ZHENG Hong-xing,LI Li-juan.Stochastic optimization on parameters of water quality model[J].Geographical Research,2001,20(1):97-102.(in Chinese))
[11] 龙腾锐,郭劲松,冯裕钊,等.二维河流水质模型横向扩散系数的人工神经网络模拟[J].重庆环境科学,2002,24(2):25-28.(LONG Teng-rui,GUO Jing-song,FENG Yu-zhao,et al.Modulus of transverse diffuse simulation based on artificial weural network[J].Chongqing Environmental Science,2002,24(2):25-28.(in Chinese))
[12] 邹毅,朱晓萍,王秀平.一种基于混沌优化算法的混合粒子群算法[J].计算机技术与发展,2009,19(11):18-22.(ZOU Yi,ZHU Xiao-ping,WANG Xiu-ping.A hybrid PSO algorithm based on chaos optimization[J].Computer Technology and Development,2009,19(11):18-22.(in Chinese))
[13] 康瑞龙.一种新型的智能优化算法:人工根系算法[D].西安:长安大学,2013.(KANG Rui-long.A new intelligent optimization method-artificial root optimization[D].Xi′an:Chang′an University,2013.(in Chinese))
[14] Kennedy J,Eberhart R C.Particle swarm optimization[C].In:IEEE International Conference on Neural Networks,Perth,Australia,1995(4):1942-1948.
[15] Eberhart R,Kennedy J.A new optimizer using particle swarm theory[C].In:Proc of the Sixth International Symposium on Machine and Human Science,Nagoya,Japan,1995:39-43.
[16] Lovbjerg M,Rasmussen T K,Krink T.Hybrid particle swarm optimization with breeding and subpopulations[C].In:Proc of the Third Genetic and Evolutionary Computation Conference,San Francisco,USA,2001.
[17] Higashi N,Iba H.Particle swarm optimization with Gaussian mutation[C].In:Proc of the Congress on Evolutionary Computation,2003:72-79.
[18] 高鹰,谢胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用.2004(1):47-50.(GAO Ying,XIE Sheng-li.Particle swarm optimization based on simulated annealing[J].Computer Engineering and Application,2004(1):47-50.(in Chinese))
[19] 池元成,方杰,蔡国飙,等.基于差分进化和粒子群优化算法的混合优化算法[J].计算机工程与设计.2009,30(12):2963-2966.(CHI Yuan-cheng,FANG Jie,CAI Guo-biao,et al.Hybrid optimization based on differential evolution and particle swarm optimization[J].Computer Engineering and Design,2009,30(12):2963-2966.(in Chinese))
[20] 张智星,孙春在.神经-模糊和软计算[M].西安:西安交通大学出版,2000,131-135.(ZHANG Zhi-xing,SUN Chun-zai.Neuro-fuzzy and soft computing[M].Xi′an:Xi′an Jiaotong University Press,2000,131-135.(in Chinese))
[21] Singh S K,Beck M B.Dispersion coefficient streams from tracer experiment data[J].Journal of Environmental Engineering,2003,129(6):539-546.
