基于VMD和快速谱峭度的滚动轴承早期故障诊断

任学平，李攀，王朝阁

(内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

滚动轴承的运转精度较高，在运转过程中反应工作状态信息的能量非常微弱，通常还伴有其他频率噪声的干扰，造成早期故障的振动特征不易被提取[1]。变分模态分解(Variational Mode Decomposition，VMD)是近几年新提出的一种自适应分解方法[2]，其摒弃了传统递归式的分解方法，采用非递归式的分解方式有效避免了分解终止条件的确定和边界效应等问题[3]。文献[4]将VMD与1.5维谱结合应用于轴承故障诊断中，成功提取到故障特征频率；文献[5]则将VMD与增强能量算子结合，也成功识别出了轴承故障。

共振解调法是故障诊断领域中比较常用的方法，其将轴承作为谐振体，从而放大轴承故障冲击产生的高频共振响应。该方法中带通滤波器参数的设置是一个关键问题，通常需要丰富的经验[6]。文献[7]将谱峭度作为STFT窗口的函数去得到最优滤波器的参数，提出了峭度图的概念，并将其应用于故障诊断领域，但存在耗时长的缺点。快速谱峭度(Fast Spectral Kurtogram，FSK)[8]不仅保留了峭度谱的优点，还弥补了谱峭度方法计算时间太长的缺点[9]。因此，针对轴承早期故障信号中噪声干扰严重，故障频率难以提取的问题，提出了基于VMD降噪与快速谱峭度的轴承早期故障诊断方法。

1 基础理论介绍

1.1 变分模态分解

VMD处理信号的过程中，IMF分量被定义为一个调幅-调频信号，并且每个分量都是具有中心频率的有限带宽。VMD算法可以分为构造变分问题和求解变分问题[10]，构造变分问题的具体步骤如下：

1)对所有的模态函数uk(t)进行Hilbert变换

(1)

2)将得到的解析信号与一个预估中心频率e-jωkt相混合，将uk(t)的频谱变换到基频带上

(2)

3)通过频移信号梯度平方L2范数估计各个模态的带宽，最后得受约束的变分问题的表达式，即

(3)

式中：{uk}为VMD分解的模态分量；{ωk}为各分量的中心频率。

为了求解，将二次惩罚因子α和Lagrange乘法算子引入受约束的变分问题中，将其变成非约束问题，表达式为

(4)

采用乘法算子交替方向算法求解式的“鞍点”获取(3)式的最优解。VMD算法的实现过程如图1所示，在求解过程中，确定每个IMF分量的中心频率和带宽，进而可以自适应地将信号的频率分离。

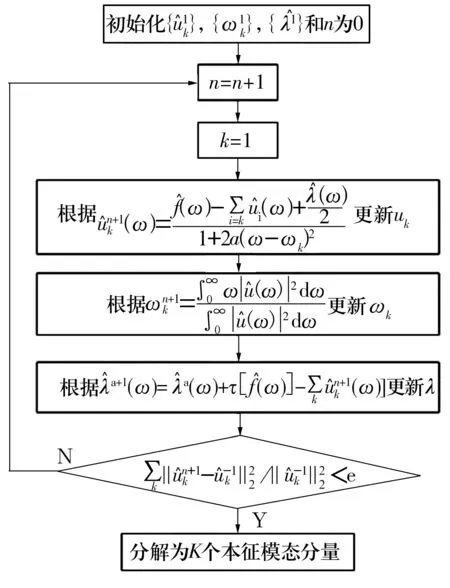
图1 VMD算法流程图

1.2 快速谱峭度

谱峭度在频域分析和高阶谱的基础上发展而来，通过计算频域内各条谱线的峭度值检测瞬态信号，并定位其所在的位置[11]。假定Y(t)是信号X(t)的机理响应，表达式为

(5)

则X(t)的谱峭度定义为

(6)

(7)

式中：H(t,f)为时变传递函数；S2nY(f)为2n阶谱矩。

为节省计算时间，快速应用于工程实际中，可采用塔式快速谱峭度图法[8]，根据快速谱峭度图上颜色的深浅来获取最优带宽及其中心频率。

1.3 基于VMD和快速谱峭度的故障诊断方法

在实际工况环境下，噪声的干扰比较严重，轴承故障早期的冲击信号比较微弱，直接识别故障比较困难。因此，提出了基于VMD与谱峭度的诊断方法，具体流程如图2所示。

2 实例分析

采用Spectra Quest公司的轴承故障模拟试验台(图3)进行试验。左侧为驱动装置，右侧为一个简单的转子试验台，加速度传感器安装在电动机侧轴承座的水平、垂直和径向3个方向。试验轴承为ER-12K型深沟球轴承，具体参数见表1。采样频率24 kHz，采样点数12 000，转速2 100 r/min，转频35 Hz，计算得外圈故障特征频率为106.7 Hz。

图2 诊断流程图

图3 故障模拟试验台

表1 ER-12K轴承具体参数

采集到的轴承故障信号的时域波形如图4所示，波形图中的噪声干扰严重，冲击特征不明显。根据中心频率相近原则[3]选取最佳分解层数K=7，VMD算法的处理结果如图5所示。

图4 时域信号

各IMF分量的峭度值计算结果见表2，依据峭度准则，峭度值大于3的分量保留了原始信号中最多的冲击特征，因此选取峭度值大于的IMF5，IMF6，IMF7分量进行重构，重构信号如图6所示，与原始信号相比，可以看到明显的冲击成分。

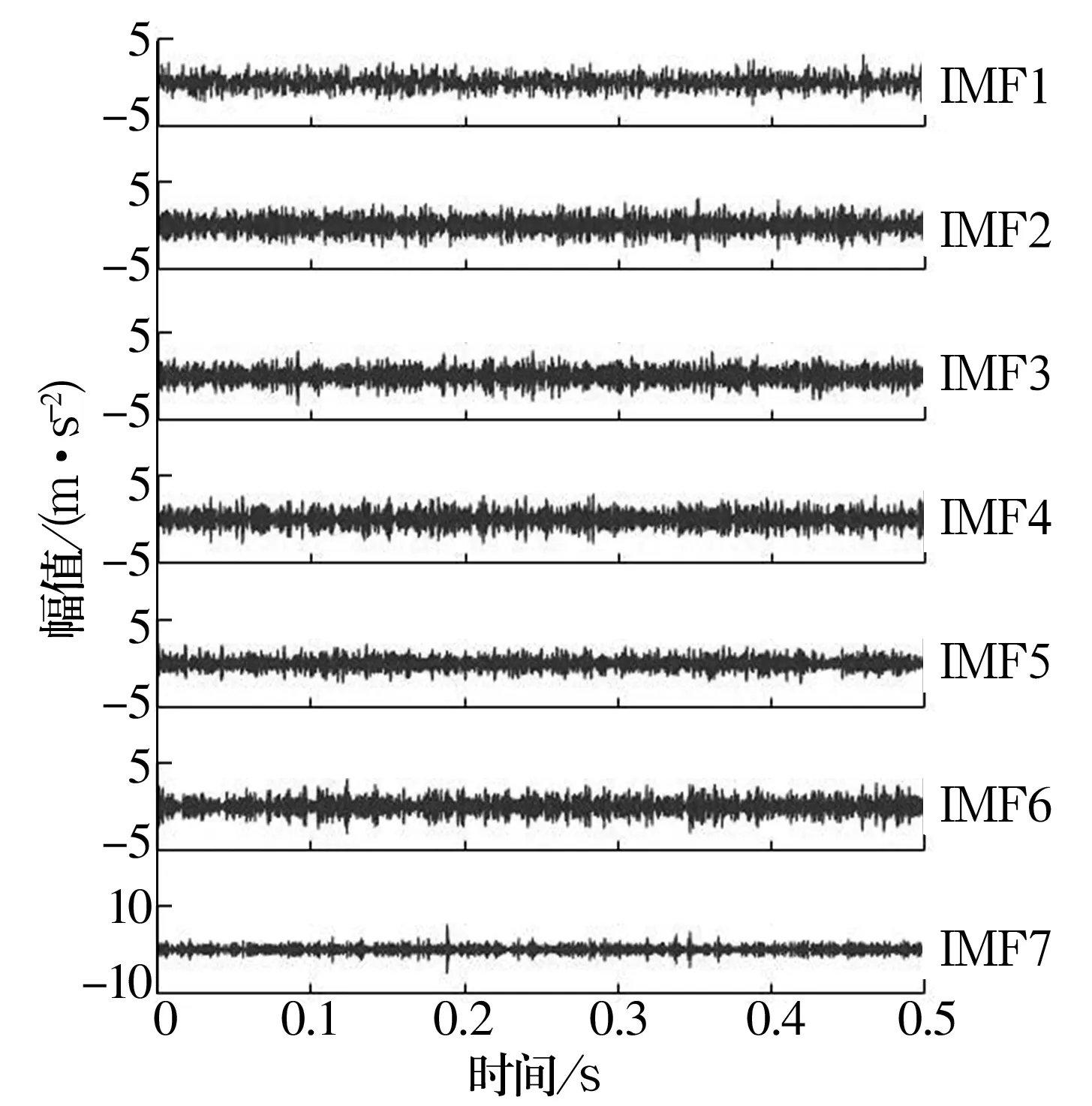
图5 VMD结果

表2 IMF各分量峭度值

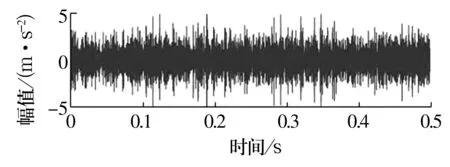
图6 重构信号

对重构信号直接进行Hilbert解调分析的结果如图7所示，虽然可在谱图中可观察到故障特征频率，但仍存在部分噪声干扰，提取效果不佳。计算重构信号的快速峭度图，结果如图8a所示。由峭度图可知中心频率为10 500 Hz，带宽为1 kHz。根据这2个带通滤波器最优参数对信号进行滤波，结果如图8b所示，与图6相比冲击成分明显增强。

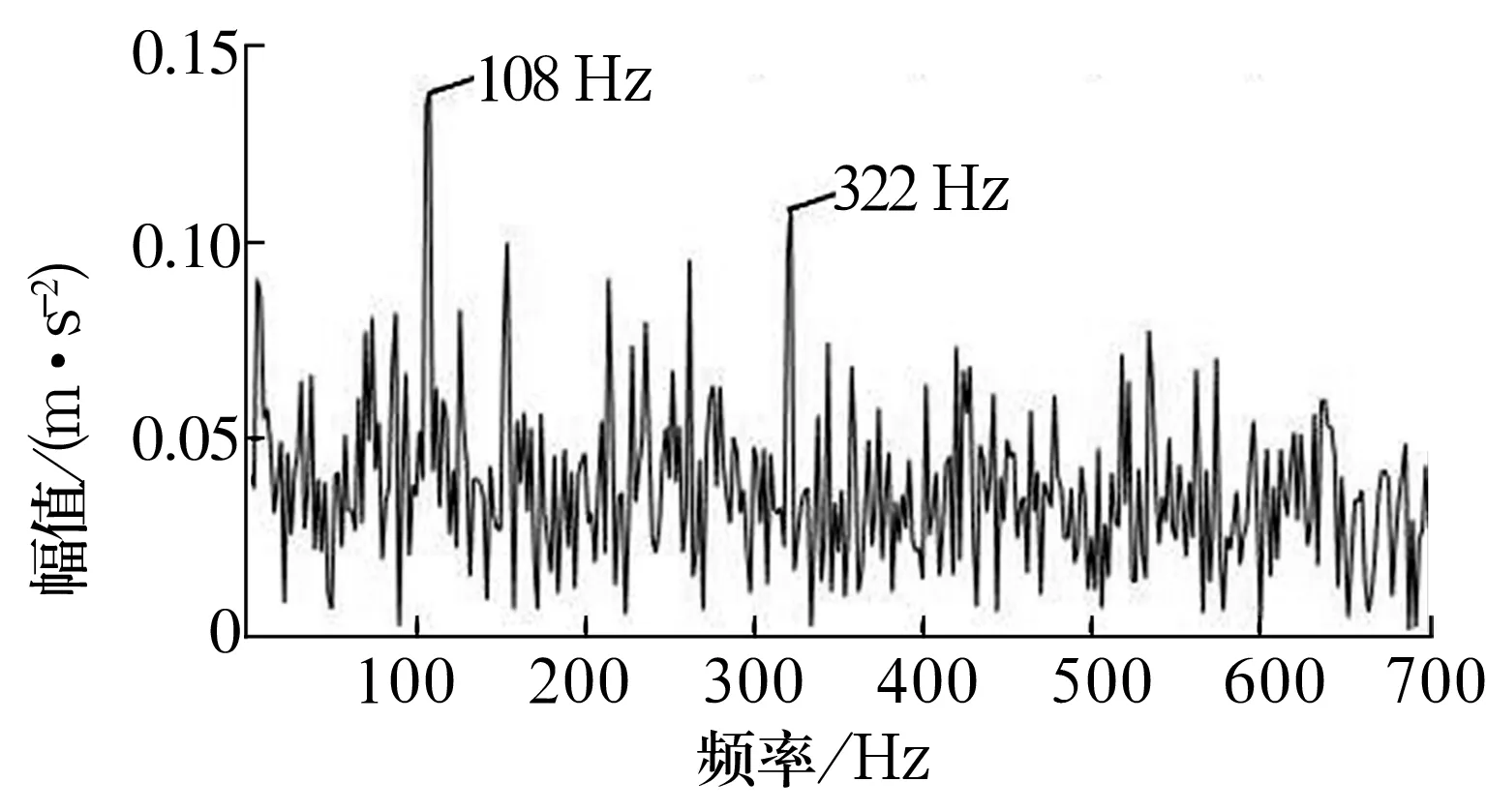
图7 重构信号的包络谱

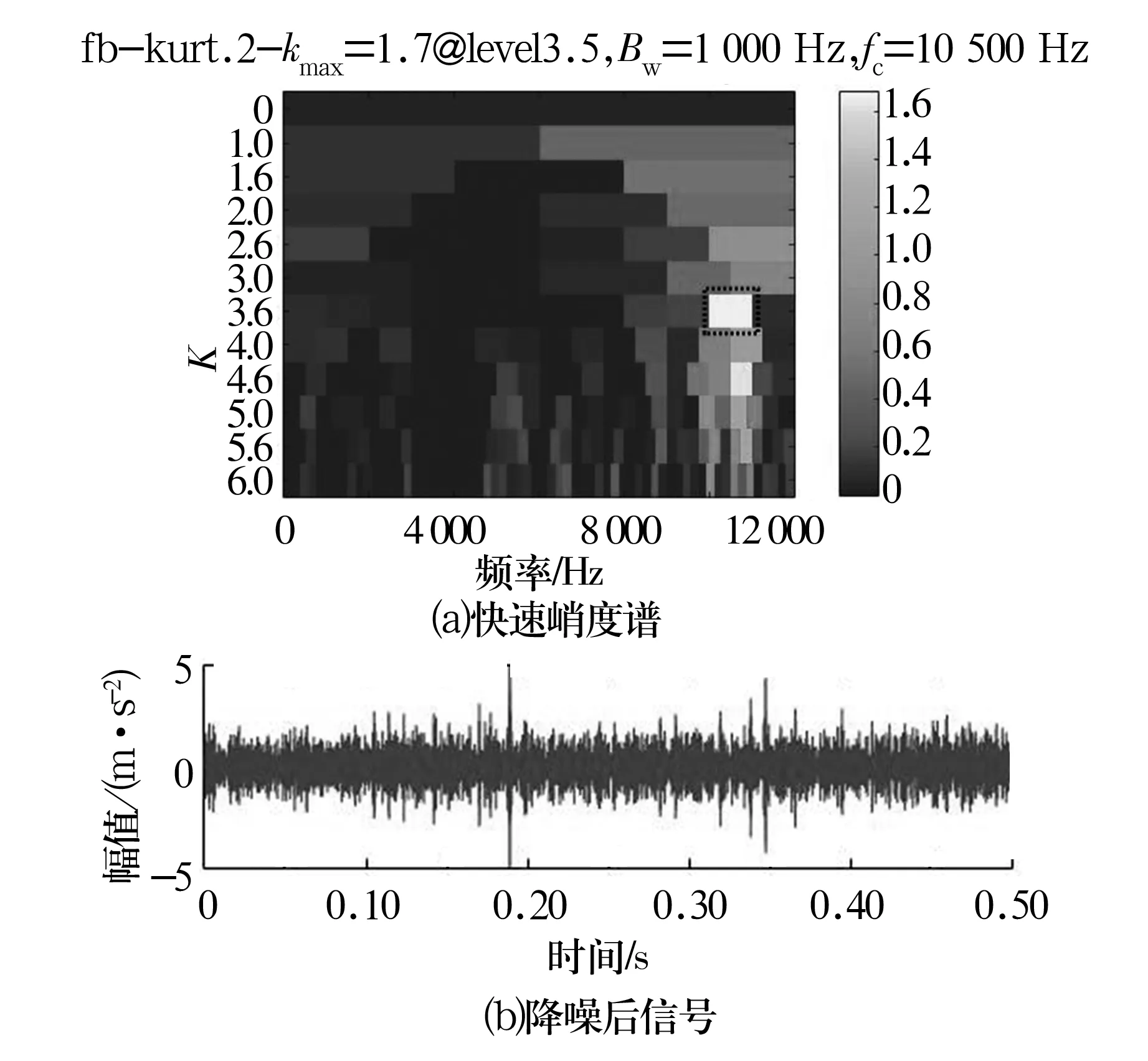
图8 快速峭度谱和降噪后信号时域波形

应用Hilbert解调方法对滤波后的信号进行解调分析，结果如图9所示，从谱图中可以观察到故障频率108 Hz及其2～5倍频，与外圈故障特征频率相符，可判定该轴承出现外圈故障。

图9 降噪后信号的包络谱

分别求出原始信号的快速峭度图和带通滤波后的包络谱如图10a所示，由原信号的快速峭度图可知中心频率为9 750 Hz，带宽为500 Hz，即带通滤波器的范围为9 500～10 000 Hz，此范围内的峭度值最大。使用带通滤波器进行滤波并对滤波后信号进行解调处理，得到如图10b所示的包络谱，从图中可以发现故障特征频率108 Hz，说明快速谱峭度方法有效；该包络谱与图7相比效果有所提升，但却不如图9所示的清晰明了，说明上述方法有效可行。

3 结束语

研究了VMD与快速谱峭度相结合的轴承早期故障诊断方法，仿真及试验数据的分析表明，该方法对于诊断轴承早期故障具有良好的效果。

图10 原始信号的快速峭度谱和降噪后信号包络谱

1)轴承早期故障信号中存在强烈的背景噪声，采用VMD方法对原始信号进行处理并结合峭度准则，从分解结果中选取敏感分量进行信号重组，减少了部分噪声成分的干扰。

2)应用快速谱峭度方法可自适应地确定带最优通滤波器的参数，避免了人为设定的不足。

3)将VMD与快速谱峭度将结合，可以精确地提取故障特征信息，与单独进行快速峭度图及包络谱分析对比说明，该方法具有一定的优越性。