产学研协同创新主体投入对其效率的影响研究

李 鹏，陈维花

（福州大学 经济与管理学院，福建 福州市 350116）

产学研协同创新主体投入对其效率的影响研究

李 鹏，陈维花

（福州大学 经济与管理学院，福建 福州市 350116）

使用2015年我国31个省市自治区的面板数据，首先分别运用DEA、SFA、因子分析对31个省市自治区的产学研协同创新的效率进行评价，然后运用TOPSIS法将三种方法的效率值综合得到31个省市自治区的产学研协同创新效率，最后运用多元回归模型实证研究产学研协同创新主要创新主体的投入对其效率的影响。结果表明：企业投入、高校投入、政府过度投入与产学研协同创新效率正相关，而政府一般投入与产学研协同创新效率负相关，科研机构投入对产学研协同创新效率的影响并不显著。

协同创新效率；TOPSIS法；多元回归模型

党的十八届五中全会提出，实现“十三五”时期发展目标，必须牢固树立并切实贯彻创新、协调、绿色、开放、共享的发展理念。创新被鲜明地摆在发展理念的首位。中央确立的创新、协调、绿色、开放、共享的发展新理念，是指导产学研协同创新的思想和行动指南。产学研协同创新是国家和区域创新体系建设的重要内容。产学研协同创新效率的高低直接关系到创新型国家建设，关系到企业自主创新能力的提升，也关系到高等教育质量的提高。对产学研协同创新绩效进行评价，分析某一创新主体的投入变化对产学研协同创新绩效的影响，有助于科学制定协同创新政策，提高协同创新绩效。目前，学者对产学研协同创新绩效方面的研究较少，就目前的研究来看主要集中在创新绩效评价指标体系构建。Bonaccorsi等［1］认为，参与产学研合作创新的各个主体具有不同的战略目标，因此，各个主体对合作所产生的效益就会有不同的预期。他们还是最早提出评价产学研合作绩效的模型。该模型是基于动机-期望的产学研合作绩效的评价模型。此模型的提出标志着学术界从理论角度关注产学研合作绩效的评价；李新荣［2］从投入产出两个方面建立了产学研合作项目的绩效评价模型，并对5个产学研合作项目进行了评价以证明其模型设计的合理性；Philbin［3］建立了一个基于转换过程的评价模型，该模型通过建立基于转换过程的投入产出要素矩阵，构建协同度评价指标体系；冯庆斌［4］构建了产学研合作创新群落分析模型，该模型从生态位、生态因子、种群关系等方面对合作创新群落进行研究，通过评价合作创新群落的投入产出比率来获知该群落的系统创新能力。首先，本文分别运用DEA、SFA、因子分析对我国31个省市自治区的产学研协同创新的效率进行评价，然后，运用TOPSIS法将前三种方法的效率值综合得到31个省市自治区的产学研协同创新效率。

1 指标选取与数据说明

1.1 指标选取

产学研协同创新中，除了企业、高校和科研机构三大核心主体之外，最重要的创新主体就是政府，所以，本文的产学研协同创新投入指标主要来自企业、高校、科研机构和政府的投入。产学研协同创新的创新产出指标用多个指标来衡量：新产品销售收入［5］、新产品开发项目数［5］和专利授权数［6］，产学研协同创新的投入和产出指标如表1所示。

1.2 数据说明

本文的研究样本为2015年我国31个省市自治区的面板数据。本文原始数据来自《中国科技统计年鉴》［7］、《中国统计年鉴》［8］以及Wind资讯软件，如表1所示。本文所选取的指标有利于降低主观指标以及调研数据所产生的统计偏误，其结果更为客观和精确。

表1 产学研协同创新投入产出指标

2 产学研协同创新的效率评价

2.1 基于DEA的效率评价

DEA由Charnes、Cooper、Rhodes三人于1978年在《欧洲运筹学杂志》发表“Measuring the efficiency of decision making units”一文正式创立［9］，它基于规模报酬不变的假设，衡量的是被评价单元的技术效率，包括了纯技术效率和规模效率，Bankeretal在此基础上放宽了规模不变的假设，经过拓展，提出了基于规模报酬可变的BC2模型，它衡量的是纯技术效率［10］。

本文应用DEAP2.1软件计算基于DEA的产学研协同创新效率，计算结果如表2所示。

表2 产学研协同创新效率（基于DEA）

2.2 基于SFA的效率评价

SFA包括成本模型和生产模型，本文选用生产模型。参照Battese&Coelli模型［11］的基本原理， 本文的研究模型设为：

其中，y表示产学研协同创新的产出，RDL表示各创新主体人员投入（人年），RDK表示各创新主体经费投入（万元），RDP表示各创新主体课题数/项目数（项）。

下标i和t分别表示各省市自治区和时间。

β0为截距项，β1，β2，β3，η和γ为待估计的参数。

vit为随机误差项，服从的正态分布；

uit为效率残差项，反映无效率的程度，反映那些在第t时期仅仅影响第i个省份的随机因素，服从的单边分布，且vit和uit相互独立。

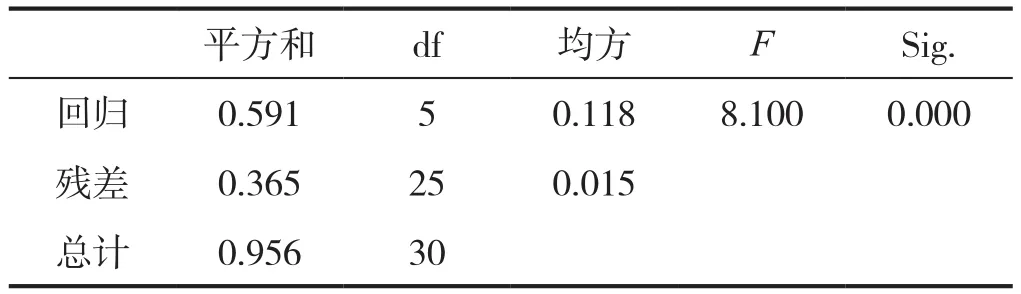
TEit表示样本中第i个省份在第t时期内的技术创新效率水平，若uit=0，TEit=1，则处于技术有效状态，若uit>0，0

δv2表示随机误差的方差，δu2表示技术效率的方差；

运用Frontier4.1程序对模型（1）进行估计。31个省市自治区产学研协同创新效率值如表3所示。效率1、效率2和效率3分别是以“新产品销售收入”、“新产品开发项目数”和“专利授权数”来表征产学研协同创新产出计算出的效率值。

表3 产学研协同创新效率（基于SFA）

2.3 基于因子分析的效率评价

因子分析效率评价方法的思想是在保证基础信息不丢失的前提下尽量对指标体系进行优化，分别计算产出的综合水平和投入的综合水平，再计算二者比值就是所求的具体效率值。

采用任娟［12］的多指标面板数据的因子分析方法，即将面板数据各个时间截面数据按时间顺序平铺展开形成一个大截面数据，并对此进行了传统因子分析。本文使用软件SPSS 18.0来完成分析。

1）适用性检验。

由于数据之间的单位存在量纲差异，首先对原始数据进行标准化处理，消除量纲不同导致的影响，然后对标准化后的产学研协同创新的投入和产出数据分别进行因子分析适用性检验，结果如表4所示。

表4 因子分析适用性检验结果

从表3可以看出，投入组和产出组的KMO检验值分别为0.693和0.763，均高于0.5，且投入组和产出组的Bartlett的球形度检验值的相伴概率均小于5%的显著性水平，从而验证了因子分析模型的适用性。

2）因子提取。

投入组和产出组的因子提取结果分别如表5和表6所示。

表5 投入组因子提取结果

表6 产出组因子提取结果

从表5可以看出，投入组共有13个因子，因子1和因子2的特征值大于1，则只需保留两个因子即可。根据表6的因子提取结果，产学研协同创新产出组共有3个因子，仅因子1的特征值大于1，且信息累计百分比保留达到 97.616%，因此，产出组只需保留一个因子即可。

3）效率值计算。

根据提取的投入组与产出组的因子数量，首先计算投入组和产出组综合因子得分，然后进行标准化处理，使两组数据介于0.1到1之间，最后用产出组标准化数据除以投入组标准化数据，确定31个省市自治区的效率值，计算结果如表7所示。

2.4 基于TOPSIS法的效率值

通过运用DEA、SFA、因子分析对我国31个省市自治区的产学研协同创新的效率进行评价，发现每个省的三种效率值都不一样且排名不一样，因此，本文使用TOPSIS法将三种效率值合成一种效率值，就是本文的产学研协同创新的效率值，如表8所示。

3 基于多元回归模型的实证分析

为了实证分析产学研协同创新的投入对产出的影响，运用多元回归模型，并应用SPSS18.0进行多元回归模型统计分析。模型设定如下：

其中，Yt表示产学研协同创新效率，通过TOPSIS法计算；c为截距；X1、X2、X3、X4分别表示企业投入、高校投入、科研机构投入和政府一般投入，都采用任娟［12］的多指标面板数据的因子分析方法计算得来，X42表示政府过度投入；β1，…，β5为模型回归系数，值为正表明提高该指标可有效提高产学研协同创新效率（数值越大，效果越显著），值为负表明该指标对产学研协同创新效率产生负效应；ξ为随机误差项，代表影响产学研协同创新效率的其他变量。

表7 各省市自治区的创新效率

表8 产学研协同创新效率

3.1 相关性分析

产学研协同创新效率和产学研协同创新投入的相关系数矩阵如表9所示。

一般讲，相关系数超过0.8的变量在分析时存在多重共性线问题。表8中产学研协同创新效率和产学研协同创新投入的相关系数最高为0.228，均小于0.8，故模型中产出变量与各个投入变量之间不存在多重共线问题，可以进行多元线性回归分析。

表9 Pearson相关性分析

3.2 有效性分析

模型有效性分析结果如表10所示，可以看出模型的R2值达到0.618，调整后的R2值是0.542，均高于0.4，说明了回归模型的有效性。

表10 模型有效性分析

3.3 方差分析

模型方差分析结果如表11所示，模型的F值为8.1，其统计显著性低于0.05的显著性水平，可以认为产学研协同创新投入与产学研协同创新绩效之间存在线性关系。

表11 模型方差分析

3.4 参数估计

运用SPSS18.0对模型（2）进行线性回归，模型的参数值估计和参数显著性结果如表12所示。

表12 模型参数估计及其显著性计算结果

通过分析表12所示的模型参数估计及其显著性计算结果可以得出以下结论：

1） 企业投入、高校投入、政府一般投入、政府过度投入的回归系数分别为0.129、0.255、-1.476、0.037，且其统计显著性分别为0.000、0.014、0.001、0.009，均在5%的水平下具有显著统计性，也说明上述四个变量对产学研协同创新效率的作用显著。进一步的分析发现：企业投入、高校投入、政府过度投入与产学研协同创新效率正相关，而政府一般投入与产学研协同创新效率负相关，说明企业投入、高校投入、政府过度投入有助于提升产学研协同创新绩效，而政府一般投入抑制产学研协同创新绩效的提升，因此，政府要加大在产学研协同创新中的投入。

2）科研机构投入的回归系数为0.195，且其统计显著性为0.155，高于0.1的显著性水平，说明不具有统计显著性，也说明尽管科研机构投入对产学研协同创新效率的影响是正向的，但作用并不显著。

3.5 稳健性检验

为了验证模型及相关性关系的稳健性，做替代变量检验。以工业增加值代替TOPSIS法计算的产学研协同创新效率，重新进行多元回归分析。如表13所示。

表13 稳健性检验

结果表明，企业投入、高校投入、政府过度投入与产学研协同创新效率正相关，而政府一般投入与产学研协同创新效率负相关，科研机构投入对产学研协同创新效率的影响并不显著，该模型的解释度进一步验证了上面的结论。

4 结论

本文利用2015年我国31个省市自治区的相关面板数据，首先，分别运用DEA、SFA和因子分析对我国31个省市自治区的产学研协同创新效率进行评价；然后，运用TOPSIS法将三种方法的效率值综合得到31个省市自治区的产学研协同创新效率，发现排在前三名的是浙江、广东、江苏，全国平均效率约为0.397，和新疆产学研协同创新效率相当，说明我国产学研协同创新的发展还有很大的提升空间；最后，运用多元回归模型实证研究产学研协同创新主要创新主体的投入对产学研协同创新效率（TOPSIS法计算）的影响，得到如下结论：企业投入、高校投入和政府过度投入与产学研协同创新效率正相关，即有助于提升产学研协同创新绩效；但政府一般投入与产学研协同创新效率负相关，即抑制产学研协同创新绩效的提高，因此，政府要加大在产学研协同创新中的投入；科研机构投入对产学研协同创新效率的影响是正向的，但作用并不显著。

［1］ BONACCORSI A，PICCALUGA A. A theoretical framework for the evaluation of university-industry relationships［J］.R&D Management，1994，24（3）：229-247.

［2］ 李新荣．基于集对分析的高校产学研合作项目绩效评价方法与 模型研究［J］．科技管理研究，2013（2）：85-88.

［3］ PHILBIN S.Process model for university‐industry research collaboration［J］. European Journal of Innovation Management，2008，11（4）：488-521.

［4］ 冯庆斌.基于群落生态学的产学研合作创新研究［D］.哈尔滨：哈尔滨工程大学，2006.

［5］ 肖文，林高榜.政府支持、研发管理与技术创新效率：基于中国工业行业的实证分析［J］.管理世界，2014（4）：71-80.

［6］ 赖永剑，贺祥民.金融发展与区域创新绩效的非线性关系：基于面板平滑转换回归模型［J］.华中科技大学学报（社会科学版），2015（2）：92-99.

［7］ 国家统计局科学技术部.中国科技统计年鉴［M］. 北京：中国统计出版社，2016.

［8］ 中华人民共和国国家统计局.中国统计年鉴［M］. 北京：中国统计出版社，2016.

［9］ CHARNES A，COOPER W，RHODES E.Measuring Efficiency of Decision - Making Units［J］.European of Operatinal Research，1978，2（6），428-449.

［10］ BANKER R D，CHARNES A，COOPER WW. Some models for estimating technical and scale efficiencies in data envelopment analysis［J］. Management Science，1984（30）：1078-1092.

［11］ BATTESE G E，COELLI T J.A model for technical inefficiency effects in a stochastic frontier production function for panel data［J］. Empirical Economics，1995，20（2）：325-332.

［12］ 任娟.多指标面板数据融合聚类分析［J］.数理统计与管理，2013，32（1）：57-67.

Research on the Influence of Input towards the Efficiency of Industry-University-Research Collaborative Innovation

LI Peng，CHEN Weihua
（School of Economics and Management，Fuzhou University，Fuzhou Fujian 350116，China）

s：Using the panel data of 31 provinces and autonomous regions in China in 2015，we first use DEA，SFA and factor analysis to evaluate the efficiency of the Industry-University-Research(I-U-R) collaborative innovation in 31 provinces and autonomous regions in China，and then the efficiency values of the first three methods are integrated into the 31 provinces and autonomous regions' efficiency of the I-U-R collaborative innovation by using the TOPSIS method.Finally，the multiple regression model is used to study the influence of the input of the main innovation subject on the efficiency of the I-U-R collaborative innovation. The results show that there is a positive correlation between the input of the enterprise，the input of the university，the excessive input of the government and the efficiency of the I-U-R collaborative innovation. The general input of the government is negatively related to the innovation efficiency of the I-U-R collaborative innovation，and the influence of the scientific research institutions on the efficiency of the I-U-R collaborative innovation is not significant.

collaborative innovation efficiency；TOPSIS method；multiple regression model

C931

A

1672-6138（2017）03-0021-07

10.3969/j.issn.1672-6138.2017.03.006

［责任编辑：曹娜］

2017-05-05

李鹏（1990—），男，湖北荆门人，硕士研究生，研究方向：创新管理与评价。