圆锥滚子贯穿式超精研加工特性分析

2017-07-25薛进学杨柏松王李娜张颖

轴承 2017年6期

薛进学，杨柏松，王李娜，张颖

(河南科技大学机电工程学院，河南洛阳 471003)

圆锥滚子是滚动轴承关键零部件，滚子凸度对滚子质量至关重要[1]。理论分析及试验验证表明对数曲线凸度为最佳[2]，对改善滚子与滚道接触应力分布有积极作用，对提高轴承寿命有重要意义[3-4]。超精研是加工出滚子凸度并保证凸度质量的重要工序[5]，贯穿式超精研是凸度加工主要方式。目前油石加工机理研究较少，贯穿式超精研大多依靠经验，理论模型及试验数据缺乏，深入分析滚子凸度形成机理任重道远。

基于超精研工艺特性，将圆锥滚子超精研看作是滚子与油石接触面相互研磨的过程[6-7]，滚子凸度的形成看作是滚子表面不均匀磨损的结果[8]。微观上，油石磨刃分布状况是影响滚子材料去除率的主要因素之一，未变形切削厚度直接影响切削比能、工件表面残余应力及表面粗糙度。借鉴砂轮磨削建模方法，基于国内外部分试验数据及经验参数，对滚子与油石接触面形状、油石动态有效磨刃分布及未变形切削厚度进行计算与分析。为进一步研究油石磨削力、滚子材料去除率，分析变姿态贯穿式超精研加工机理做准备。

1 贯穿式超精研加工方式

圆锥滚子贯穿式超精研加工如图1所示，2个导辊做定轴同向旋转，滚子在导辊的驱动下小端在前、大端在后，自旋贯穿通过导辊，油石以一定的压力作用在滚子上，沿轴向做高频往复振荡。油石超精研面不修整，其形状由超精研过程决定。贯穿式超精研分为定姿态贯穿和三段式贯穿2种，定姿态贯穿又分为正置定姿态和斜置定姿态。超精研区滚子直径的不断变化引起油石与滚子相对速度、接触面形状、接触压力等多个因素的变化。三段式贯穿超精研中，滚子姿态的不断变化同样引起多个因素的变化。

图1 圆锥滚子贯穿式超精研加工示意图Fig.1 Diagram of through-feed superfinishing of tapered roller

贯穿式超精研滚子凸度受多种因素影响，且各因素之间存在复杂关联，建模分析难度大。在掌握贯穿式超精研基本特征，不影响模型正确性的前提下做出假设：1)加工滚子过程中，油石加工面是直径不变的内圆柱形曲面，直径等于滚子大端直径；2)将滚子沿轴向均匀分割成宽度足够小的薄片，当切片宽度足够小，各切片两端直径差可以忽略不计，每个切片可以视为一个圆柱体(图1b)。

基于上述假设，油石与滚子接触视为直径不变的内圆柱与众多直径渐变的外圆柱接触。先单独分析一个滚子切片与油石的接触状态，再以此为基础对整个滚子与油石的接触状态进行分析。

2 周向接触弧长分析

周向接触弧长是圆周方向接触弧长的简称，指油石与滚子瞬时接触弧长。周向接触弧长在加工过程中动态变化，受诸多因素的影响，这里借鉴砂轮内圆磨削几何证明方法，得到分段式周向接触弧长基础模型，在此基础上引入实际加工经验和国内外参考文献给出的一些参数对模型进行修正。

2.1 周向接触弧长几何分析

油石与滚子接触状态如图2所示，图中：rw为滚子半径；rs为油石超精研面半径；φ为滚子在极短时间内转动的角度；Δz为分割切片的宽度。磨粒位置在图2a平面内没有任何位移，滚子旋转引起磨粒对滚子研磨，研磨速度等于滚子旋转线速度。在图2b平面内油石沿z轴高频振荡和滚子沿z轴贯穿共同引起磨粒对滚子研磨，研磨速度是二者速度的叠加。油石振荡速度比滚子贯穿速度大，当振荡方向和贯穿方向一致时，叠加速度等于振荡速度减去贯穿速度，反之叠加速度等于二者相加。

图2 滚子与油石接触状态示意图Fig.2 Diagram of contact status between roller and oilstone

根据以上分析，当滚子旋转角度为φ，磨粒的运动轨迹方程为

(1)

式中：nw为滚子旋转速度；fa为滚子贯穿速度；vs为油石振荡平均速度，当油石振荡方向与滚子轴向贯穿方向一致时取“-”，方向相反时取“+”；A为油石振幅；f为油石振荡频率。

油石振荡曲线视为正弦曲线，则运动速度为其导数余弦曲线，因此油石振荡平均速度为4Af/60。滚子旋转φ角，磨粒在z轴方向位移是油石振荡位移和滚子沿轴向贯穿位移的叠加，而振荡方向成周期性变化，因此z轴方向位移如(1)式所示。

(2)

式中：ψ为油石与滚子的接触角，与油石切入加工表面深度、油石与滚子的弹性变形直接相关。先不考虑弹性变形，用几何理论推导公式，在此基础上再考虑弹性变形，引入变形系数。

滚子与油石接触的平面示意图如图3所示，as为油石切入加工表面深度，由径向压力、接触面积、油石及滚子的材料性质等因素决定，可由试验测得。由于as的值较小，与as相关的ψ很小，利用近似原理及几何关系得到ψ的近似计算公式为

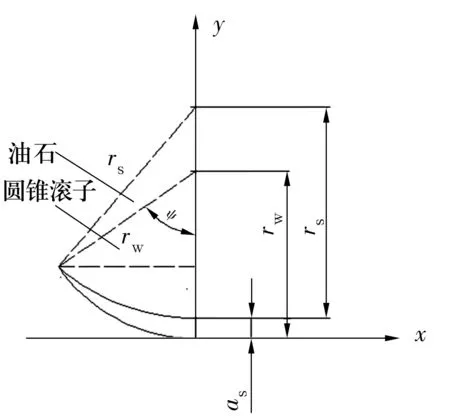
图3 滚子与油石接触角示意图Fig.3 Diagram of contact angle between roller and oilstone

(3)

式中：ds为油石加工面直径；dw为离散化滚子直径，取值为滚子大端直径与小端直径之间。将(3)式代入(2)式得到完整的周向接触弧长计算公式为

(4)

考虑弹性变形对ls的影响,在超精研过程中滚子受到油石的径向压力，二者均会发生微量弹性形变引起周向接触弧长发生变化。在砂轮磨削中，砂轮直径较大且与工件的径向接触应力较大，试验证明实际周向接触弧长是理论周向接触弧长的1.3～2.3倍[9]。与砂轮磨削相比，油石的尺寸小且径向接触应力小，弹性变形量要小得多，但为了保证计算精度，在此引入一个大于1的系数kt(精确取值可通过试验得到)。

超精研中，与油石振荡速度vs相比，滚子贯穿速度fa很小，滚子贯穿运动对超精研影响不大，为了让模拟图简单直观，在可接受范围内忽略fa对ls的影响，令[dw(ds-dw)]/ds=de。根据以上分析，最终整理得到周向接触弧长为

(5)

2.2 周向接触弧长影响因素分析

由上述周向接触弧长公式的证明和分析可知，ls受诸多因素的影响且各因素对其影响程度和影响效果不尽相同。

根据参考文献[8-10]设定分析参数，在kt=1.3，A=1 mm， 8≤dw≤10 mm，ds=10 mm下， MATLAB模拟结果如图4所示。

由图4可知，周向接触弧长ls随着圆锥滚子直径dw的增大而增大，并且从滚子小端到中间部分ls增大的速率较慢，在滚子大端ls增大的速率变快，越接近滚子大端，ls增大的速率越快。这一趋势不受其他参数取值的影响，甚至变化速率也不受各参数的影响。这是因为：油石加工面是直径等于滚子大端直径的圆弧曲面，随着dw不断增大，超精研区滚子外形与油石加工面贴合程度逐渐提高，而两者贴合程度越高ls越大。整个超精研接触面像一个“几”字形，这一理论分析结果符合预期。

图4a中，在dw相同处ls随圆锥滚子旋转速度nw的增大而减小，但变化幅度不大，说明nw对ls的影响不是很显著。从相邻2条曲线之间的距离可以看出，ls随nw增大而减小的速率逐渐变慢。

图4 各参数对周向接触弧长ls的影响Fig.4 Effect of parameters on circumferential contact arc length ls

nw增大意味着滚子与油石相对速度增大，即接触面积必然减小，但是相对速度增大对接触面积的影响是非线性的，当相对速度大到一定程度，接触面积基本上不再增长。

图4b中，在dw相同处，ls随油石切入加工表面深度as的增大而增大，且变化较明显，说明as对ls的影响非常显著，这一结论与实际情况完全相符。另外，从相邻2条曲线之间的距离可以看出，ls随as增大而增大的速率基本保持不变。as是影响ls取值的关键参数中较容易改变的一个，对分析凸度形成机理具有重要意义。

图4c中，在dw相同处，ls随油石振荡频率f的增大而增大，变化不是很明显，说明f对ls的影响不显著。从相邻2条曲线之间的距离可以看出，ls随f增大而增大的速率基本保持不变。这是因为：f增大引起z轴方向的值增大，进而引起ls增大；同时，f增大，滚子与油石相对速度增大，导致接触面积减小：2种影响相互作用最终导致f对ls的影响不显著。

3 磨刃数计算与分析

3.1 磨刃数模型建立

在油石表面，磨粒高度分布参差不齐，沿油石加工表面径向确定油石切入加工表面深度as，则可以认为只有包括在该切入深度范围内的磨粒才能真正参与超精研，不在该范围内的磨粒由于高度不够而没有办法参与，因此真正参与超精研过程的油石磨粒与油石表面磨粒数相比要少得多。试验表明，单位长度静态有效磨刃数Nt与as直接相关但不是线性关系。Nt随着as增大而增大，且增大速率不断加快；在as达到某一临界值时，Nt增大速率达到最大；之后Nt增大速率逐渐变慢，最终Nt的值趋于稳定。Nt的计算公式为

(6)

式中：c1为与油石磨刃密度有关的系数；ks为与油石磨刃形状有关的系数；p为指数。单位长度指轴向单位长度。

当油石相对于滚子运动时，部分磨粒的运动轨迹被其前方磨粒的运动轨迹覆盖，导致这部分磨粒没有办法参与加工，因此动态有效磨刃数比静态有效磨刃数少，在此引入一个小于1的动态系数kd(具体取值可以通过试验得到)。则在长度为ls的接触弧上，动态有效磨刃数Nd计算公式为

Nd=kdNtls。

(7)

3.2 动态有效磨刃数的计算与分析

根据参考文献[8-10]设定分析参数，取c1=4 420 mm2，ks=1，kd=0.6，p=1.5。MATLAB模拟结果如图5所示。

图5 切入加工表面深度as对动态有效磨刃数Nd的影响Fig.5 Effect of cutting surface depth ason dynamic valid cutting edge number Nd

由图5可知，动态有效磨刃数Nd随滚子直径dw增大而增大，并且从滚子小端到中间部分Nd增大的速率较慢，在滚子大端Nd增大的速率迅速增加，整体趋势和周向接触弧长ls相似。不同的是，dw-Nd曲线在滚子小端和中间部分显得更加平坦即变化幅度更小，到滚子大端附近Nd迅速增大。从(6)式和(7)式也能明显看出as在所有关键参数中的特殊性，即as与Nd呈指数关系。

在dw相同处，Nd随油石切入加工表面深度as的增大而迅速增大，说明as对Nd的影响非常显著，可以通过小幅度改变as来显著影响Nd，从而引起滚子材料去除率的变化。在同一个滚子超精研过程中，要使滚子素线出现凸度，即滚子轴向各部分材料去除率呈一定规律性变化，就必须保证Nd相应地呈一定规律性变化。理论上来看，只需要改变一个或者几个关键参数来影响Nd，选择性非常多。但是在实际加工中，在同一个滚子经过油石的过程中，改变其他关键参数的难度很大。而通过改变导辊曲面形状来控制滚子运动轨迹，进而控制滚子轴向各部分as的值来改变Nd值是完全可行的。

按照上述方法，通过改变导辊曲面形状使滚子沿轴向走一条上下运动的波浪线，即as的值成为随dw先均匀减小后均匀增大的变量。各参数取值同上，MATLAB模拟结果如图6所示。

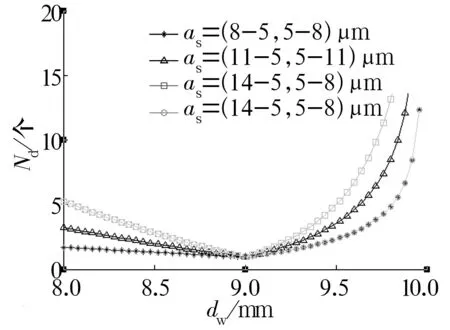
图6 切入加工表面深度渐变对动态有效磨刃数的影响Fig.6 Effect of gradual change of cutting surface depth on dynamic valid cutting edge number

由图6可知，dw=9 mm为as均匀递减和均匀递增的分界线。as在dw=9 mm处取得最小值0.005 mm，在滚子两端取得最大值，并逐渐增加滚子小端和大端as的值依次为0.008，0.011，0.014 mm。滚子两端的Nd值逐渐增大，由于中间位置as=0.005 mm始终不变，出现中间低两端高且大端明显比小端更高的“√”形结构。若要求滚子素线出现以中间为对称轴的对称凸度，滚子大端材料去除量大，小端材料去除量相对少，中间部分材料去除量最少，那么对应的越靠近两端Nd值越大，越靠近中间值越小。因此dw-Nd图像在理论上应该是类似于“√”形结构。

如果设定滚子小端和大端的as相等，大端Nd随dw增大而增大的速率明显比小端快很多。图6中其中一条曲线，小端as最大值为0.014 mm，大端as最大值为0.008 mm。在实际超精研过程中，可以分别控制两端的as来调整图像形状。文中给定的每一组as值都是先均匀递减再均匀递增的，而实际在超精研过程中要想得到标准的对数凸度，as值一定是从滚子小端到滚子大端按照一定规律逐渐过度的复杂函数。除了油石和滚子的材料性质，油石压力和接触面积是影响as取值的主要因素，而油石压力又是由滚子轨迹决定的，因此需要对此进行更加深入的量化分析和试验验证。

4 磨刃未变形切屑厚度分析

未变形切屑厚度影响磨粒受到的磨削力、比磨削能、磨削区温度，从而影响工件表面残余应力的性质、大小和分布，以及加工表面粗糙度[9]。因此，计算超精研未变形切屑厚度，分析各影响因素对加工过程的影响至关重要。

将磨粒视为锥形磨粒，根据切削层平均体积确定单个磨刃未变形切屑最大厚度。切削层平均体积等于单位时间内被油石切去的金属体积与单位时间内油石表面参加超精研的磨刃数之比。油石磨刃运动轨迹如图7a所示，由此得到磨刃的平均切削厚度为

(8)

式中：adg为磨刃的平均切削厚度；Ndd为油石单位面积动态有效磨刃数;bdg为磨刃的平均切削宽度；vw为滚子旋转线速度。

磨粒的切削模型如图7b所示，将磨粒视为圆锥体，磨粒半锥角为θ，根据bdg/adg=4tanθ=C及agmax=2adg，得到磨刃未变形切屑最大厚度为

图7 几何证明辅助示意图Fig.7 Auxiliary diagram of geometric proof

(9)

由(9)式可知，磨刃未变形切屑最大厚度受多种因素影响。agmax随油石切入加工表面深度as的增大而增大且影响效果与p直接相关；p值越大，as对agmax的影响就越大。agmax随油石振幅A、振荡频率f、滚子半径rw及旋转速度nw的增大而减小，这4个参数对agmax的影响效果完全相同，且任何一个参数增大都意味着滚子与油石相对速度增大，从而引起agmax减小。同时，agmax随磨粒半锥角θ的增大而减小。通过(9)式可以量化分析各关键参数对agmax的影响，为进一步研究超精研过程磨粒受到的磨削力、比磨削能、工件表面残余应力及粗糙度等奠定基础。