三维裂纹前缘参数化网格模型研究

侯乐毅，唐俊星

(1.中航工业金城南京机电液压研究中心，南京211106；2.西北工业大学动力与能源学院，西安710072)

三维裂纹前缘参数化网格模型研究

侯乐毅1，唐俊星2

(1.中航工业金城南京机电液压研究中心，南京211106；2.西北工业大学动力与能源学院，西安710072)

为实现三维疲劳裂纹扩展自动模拟及获得更高精度的应力强度因子，在实体参数化建模的基础上，自编程开发了两种参数化裂尖网格模型，分别对应奇异元法和虚拟裂纹扩展法(VCCT法)计算应力强度因子，且两种参数化网格可互换以便相互验证。两种裂纹模型均精心设计，裂纹前缘网格正交，过渡均匀，疏密可调。与解析解的对比结果表明，两种参数化网格模型均有很高的计算精度，可为一般工程结构获得较高精度的应力强度因子结果提供技术支持。

三维疲劳裂纹；裂纹扩展；虚拟裂纹扩展法；应力强度因子；参数化网格模型；奇异元法

stress intensity factor；parametric gridmodel；singular elementmethod

1 引言

应用有限元法计算三维裂纹强度因子及模拟裂纹扩展已有大量原创性成果，涌现出多种裂纹建模思路及相应裂纹模型，在众多领域有效地解决了大量的工程断裂问题。国外具有代表意义的成果有德国的ADAPCRACK3D[1]、英国的ZENCRACK[2]及美国的Franc3D[3]软件等。与其他两个软件不同的是，ADAPCRACK3D裂尖附近网格没有采用奇异单元，而是用低阶常规单元所应用的虚拟裂纹闭合法(VCCT法)获得应力强度因子。国内研究工作主要是基于通用有限元软件(如ANSYS或ABAQUS软件)进行二次开发，编制程序包，并部分程序已做到裂纹扩展自动模拟。如徐杰[4]基于ABAQUS平台与Hy⁃perMesh软件，研究了三维平片裂纹扩展模拟技术，并开发了AxDPFlow程序，裂纹建模效率得到提高，但其应力强度因子沿裂纹前缘变化还不够光顺，精度还可进一步提升；唐俊星等[5]基于ANSYS平台用APDL语言进行二次开发，实现了三维裂纹平片扩展自动模拟通用技术，但在裂尖网格模型方面采用了相对较简单的网格，裂纹前缘也没有采用正交网格；于培师[6]通过预先开发典型裂纹参数化子模型数据库的思路，将子模型嵌入到实体模型中或有限元模型中，实现了平片裂纹的自动模拟；贾旭等[7]为避应力状态假设，应用应力拟合法计算应力强度因子。陈景杰等[8]比较了20节点和12节点奇异元这两种有限元模型，研究了应力强度因子对裂尖网格参数的敏感性。俞树荣等[9]通过奇异元法建立表面裂纹模型，研究了应力强度因子对表面裂纹扩展的影响。齐桂营[10]进行了具有倾斜裂纹的CTS试样三维断裂行为的研究，其裂纹前缘过渡网格具有特色，亦是采用的VCCT法计算应力强度因子；此外，林晓斌[11-12]、Shivakumar[13]、Rybicki[14]、樊鸿[15]等也对疲劳裂纹和应力强度因子进行了大量研究，获得了丰硕成果。由于这些研究成果各自的三维裂纹建模方法及相关细节不同，这些方法和程序在繁杂度、工程通用性、掌握的难易程度、效率与计算精度方面各有差别。

进行裂纹扩展模拟常常遇到的难点有：①含裂结构有限元建模过程比较繁杂，往往需人工干预，重复性工作量大，有时还需要与外围前处理软件进行数据交换，工程应用效率低。②部分裂纹模型几何类型通用性较差，针对具体几何尺度的特定结构相对容易实现裂纹建模和扩展模拟，但编制适用程序比较难，能普遍适用于各种复杂工程结构或各种不同类型的裂纹问题的模型较少。③裂纹应力强度因子计算精度不稳定，这主要由两方面原因产生，一方面是各模型裂纹前缘网格划分方式不同，且各种裂纹参量的获取方法对裂纹尖端附近网格质量的敏感性不一；另一方面是裂纹参量的计算精度需设计者具有一定的技巧和数值计算经验。因此，工程中需要一种建模相对简单、通用性强、精度好、掌握复杂度低、自动化程度高的裂纹扩展模拟方法。应力强度因子计算作为疲劳裂纹扩展模拟中最基本最核心问题，本文将着重探讨三维平片裂纹尖端的局部网格模型，并比较位移法和VCCT法获取应力强度因子的精度。

2 三维裂纹实体参数化模型

裂纹建模采用文献[5]提出的实体参数化建模，其基本建模思路是将完整块分割成裂纹块(由6个子块构成)和非裂块，裂纹块包裹着裂纹面，然后裂纹块与非裂块进行无缝组装，整个组装体仍可以是整个零件或其局部子块。这种组装技术可称为实体局部镶嵌技术，其组装过程如图1所示。

图1 含裂块的无缝组装Fig.1 Geometric subdivision of cracked structure

裂纹实体参数化建模的关键在于裂纹块的形成过程。裂纹块的几何形状受裂纹前缘线形状控制。首先以控制裂纹前缘的点列作为参数，创建描述裂纹的B样条曲线，并在首尾端部按斜率适当延长(以适应曲面表面)；再在裂纹前缘扩展的正、反方向形成2条间距为d的等间距线，并将d设为与裂纹前缘曲线长度L相关联的参数。针对不同类型裂纹，d与L的比值可不同，一般表面裂纹d/L可在0.025～0.050范围之间，如图2所示。然后以此3条曲线为中心，裂纹面正、反法向各复制3条间距为d的等间距线，以这9条曲线为框架，按自下而上完成6个子块建模，并通过部分关键点合并的方法将重合的上下裂纹面包裹入其中，如图3所示。最后将这6个子块与完整块进行布尔运算，形成6个裂子纹块和非裂块[5]。

图2 裂纹前缘等间距曲线Fig.2 Equidistantcurve on crack front

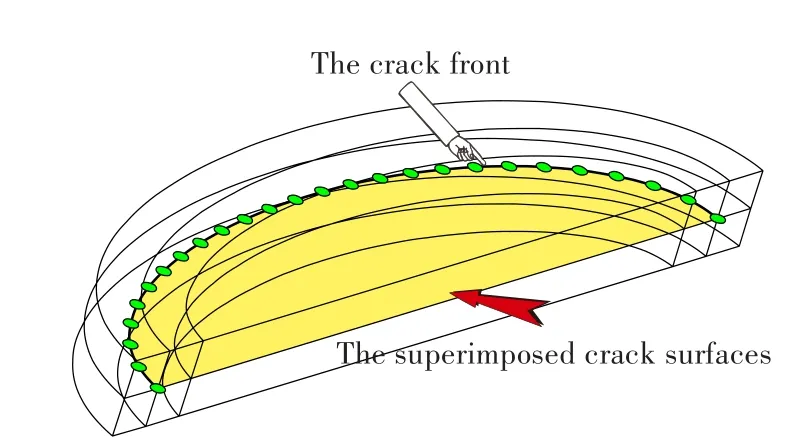
图3 包裹着的裂纹面Fig.3 Embodied crack surfacesof cracked block

这种实体的划分方式的突出优点是与裂纹相连的4个小子块为拓扑形状规则的长方体，其截面为“田”字形，裂纹前缘网格划分容易自编程实现。

本文采用的实体局部镶嵌技术特点是，同一套参数可控制局部外形不同但拓扑结构等价的不同零件裂纹建模，其几何结构通用性强。除解决结构几何适应性方面问题外，为更方便于工程应用，避免出现过多参数，降低程序复杂度，针对不同类型的裂纹，开发了相应典型裂纹程序库。不同的裂纹类型对应不同的一套参数，如将裂纹程序库类型分为表面裂纹、角裂纹、内埋裂纹、穿透裂纹、双裂纹、非平片裂纹等。各种类型裂纹扩展的模拟都将在AN⁃SYS环境中进行，不需再借用其他前后处理软件。

3 裂尖网格参数化模型

3.1 奇异元参数化网格模型

裂纹应力强度因子计算主要分为直接法和间接法。直接法中，将有限元软件获得的裂纹尖端节点位移或应力代入裂纹尖端位移渐近式可获得应力强度因子(SIF)，或由大型有限元软件内嵌程序直接输出裂纹尖端的SIF。直接法中主要有位移外推法、1/4边单(双重)中节点位移法、应力法等。节点位移为有限元计算后直接输出量，因而位移法最简单，但要获得较好精度必须要求裂纹尖端附近具有较高的网格质量。因此，当采用位移法求解应力强度因子时，常常需要配合使用1/4边中节点奇异元，以降低在裂尖附近布置大量常规单元的要求。

尽管国内外相关文献及软件出现的三维裂纹尖端网格模型各式各样，但当采用奇异元法计算裂纹应力强度因子时，其核心点基本相同：即围绕裂尖，网格通常被设计成蜘蛛网状的放射式，最靠近裂尖的一圈单元为三菱柱形，且与裂尖相连的单元边中节点被移置到边长的1/4处，形成奇异楔形单元，如图4所示。

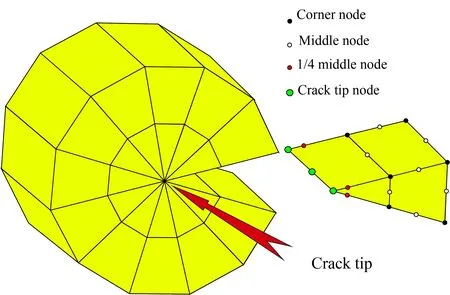
图4 裂尖通用网格模型Fig.4 Generalmeshmodelof cracked block

虽然各种文献在裂纹尖端附近网格划分思路上取得了统一，但具体划分时有关参数取值不同。如围绕裂纹虽然均是按蜘蛛网式一圈圈地布置节点，单元按一层一层如洋葱片一样有规律排列，但生成单元的层数往往不同，且围绕裂尖周向单元分割的份数也相异，常见份数有6、8、12、16、24、32、40等几种，还有各层单元之间尺寸相对比值或与裂纹尺寸的绝对比值也不尽然相同。因此，裂纹尖端附近网格划分受人为因素影响的成分较大，应力强度因子计算精度从而受之影响，给工程应用带来一定困惑。

结合本文裂纹实体模型特点及大量数值试探实验的结果，本文推荐的裂纹块参数化网格模型如图5所示。图中，与裂纹尖端相连的4个核心子块采用自编程序生成放射式网格，另2个子块ANSYS程序可采用Sweep方式自由划分，单元类型选择Solid95或Solid186。在该裂纹模型中，围绕裂纹尖端周向均匀布置24个楔形单元，相当于每个单元的楔角为15°，为ANSYS软件推荐单元形状最小角度的下限。再进一步综合考虑计算精度和计算效率的平衡，在田字形截面中，划分层数6～10层单元，各层单元尺寸大致均匀，沿着裂纹曲线方向划分50～200个单元。这样布置的单元数量适中、网格过渡均匀、单元形状比一般不超过4，既可用1/4双节点位移计算应力强度因子，又有足够多的节点适用于位移外推法。

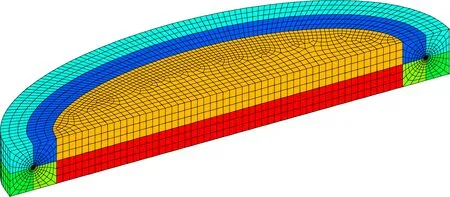
图5 裂纹块参数化网格模型Fig.5 Parametricmeshmodelof cracked block

为保证裂纹块与非裂块在边界上网格划分完全一致，先用Mesh200单元采用MAPPED方式划分两者的公共面，这些公共面上的节点即为裂纹块的边界节点。自编程序中，保留这些边界节点不再重新生成，使得裂纹块与非裂块的边界上具有公共节点，保证了两者的位移协调。

3.2 VCCT法参数化网格模型

VCCT法可采用低阶的实体单元来计算复杂的三维断裂问题[13]，其基本原理是将新开裂的裂纹面所增加的表面能等效为减少的外力势能。或者相反，新闭合的裂纹面表面能等于增加的外力势能。当然，这一新开裂(或闭合)微小尺寸的裂纹面是人为假定，因此最初的虚拟裂纹扩展法需要两步计算，计算开裂前后的外力势能差即为裂纹界面能。由于假定开裂尺寸不可能无限小，因此理论上讲VCCT法为近似间接法估算应力强度因子方法。

介于虚拟裂纹扩展法进行二次有限元分析的不便，Rybicki等[14]提出了修正的裂纹闭合积分方法，仅一次有限元计算，简称MVCCI方法。但MVCCI法需对裂纹前缘网格进行精心划分，使得虚拟裂纹扩展前后裂纹前缘位移场或节点力近似相等。

文献[10]的研究结果表明，VCCT法求解应力强度因子的精度，关键在于裂纹前缘网格尺寸及划分方式。通常，裂纹前缘网格在裂纹扩展正、负方向单元分布均匀、大小一致。同时，与二维裂纹不同，三维裂纹前缘局部可能曲率较大(图6)，造成裂纹前缘上相邻两单元边夹角 β较大程度地偏离180°(偏离越严重，扩展前后位移场相似性越难以保证)，裂纹扩展方向与单元夹角α对裂纹应力强度因子的计算精度也有一定影响。减少总体自由度数。

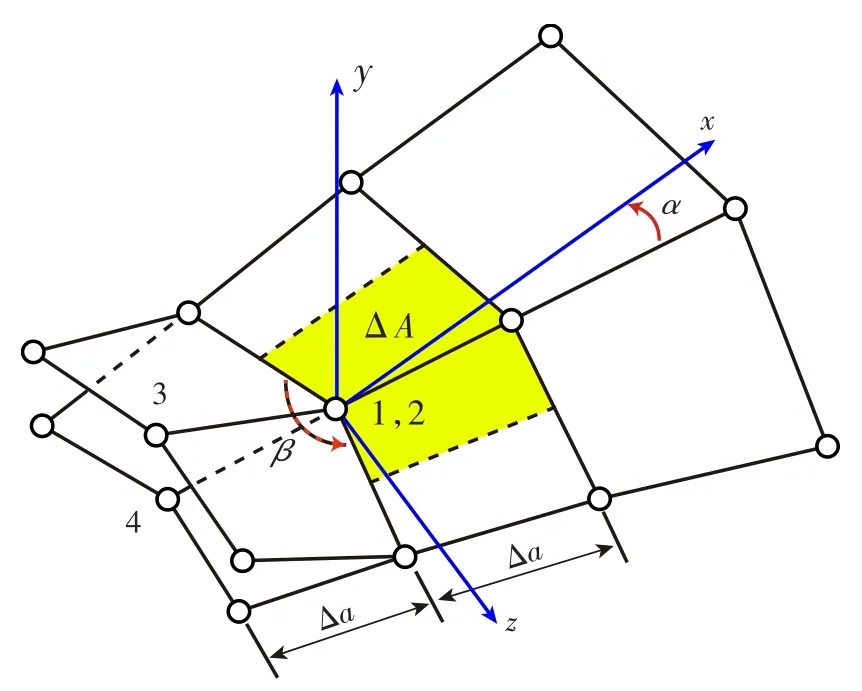
图6 曲线三维裂纹前缘局部Fig.6 Curve on local three-dimensional crack front

本文的VCCT法网格与奇异元网格通过参数控制可相互切换，而可维持非裂纹块网格相同，方便于选择不同的计算应力强度因子方法，以便相互验证。

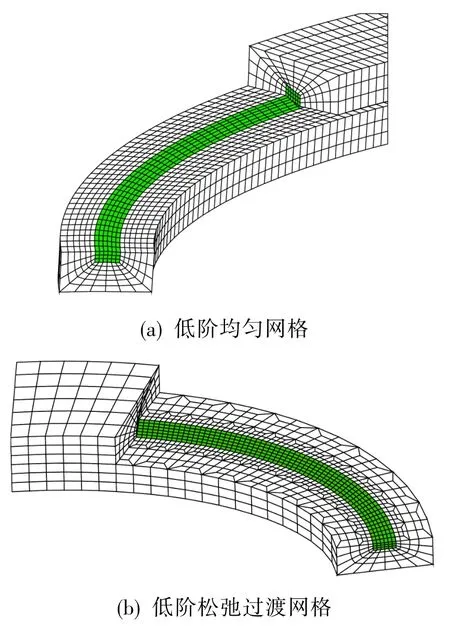
图7 VCCT法裂纹尖端参数化网格Fig.7 Virtual Crack Closure Technique for parametricmesh modelof crack tip

三维裂纹实体参数化模型在裂纹前缘附近形成4个截面大小相等的规则六面体，容易生成大小一致的网格，与VCCT法要求的均匀网格划分要求自然匹配。图7为设计的裂纹前缘网格，整个网格分为中心部位单元和外围单元两部分。中心部位被均匀划分成6×6共36个单元，且单元在裂纹扩展方向和裂纹面法向均等距，外围单元为放射式过渡单元，且中心单元的尺寸及过渡单元的圈数均设计成可调参数。而在田字边界与奇异单元边界网格划分数一致，可保持两种网格的互换性。中心单元与外围单元均采用低阶Solid45单元。为减小α与 β的影响，除在裂纹前缘形成正交网格外，还可采用局部松弛网格。采用松弛网格目的是在裂纹块边界网格与中心的36个裂尖单元间形成适当的过渡网格，有利于

4 算例

4.1 受倾斜的均匀拉伸应力作用的内埋圆裂纹算例

分别用奇异元法和VCCT法对有理论解的内埋圆形裂纹进行应力强度因子计算，以验证裂纹模型计算应力强度因子的精度。

如图8所示，一半径为a的圆形裂纹受倾斜拉伸作用，倾斜角为γ，其投影与 X轴的夹角为ω。文献[16]给出了该问题应力强度因子的解析解，文献[15]也对该问题应用有限元进行了裂纹建模分析(其计算最大相对误差为2.3%)。为便于比较，本文所取几何参数与文献[15]的一致，即内埋圆形裂纹半径为1mm，圆柱半径为20mm，圆柱高40mm。材料弹性模量为2×105MPa，泊松比为0.3，均匀拉伸载荷为100MPa。

对于该内埋裂纹，由于存在对称性，取半个圆柱体进行有限元建模(裂纹模型取γ=45°，ω=0)。采用奇异单元模型计算裂纹应力强度因子，其有限元网格见图9。奇异单元网格模型裂纹尖端采用图5所示的参数化网格，围绕裂纹周向分为24个单元，沿着裂纹前缘分100个单元。VCCT法采用图7(b)中的低阶松弛网格过渡网格，中心36个单元，过渡单元为6圈。

图8 内埋圆形裂纹受倾斜均匀拉伸作用力示意图Fig.8 Uniform slope tension effectson an internal circular crack

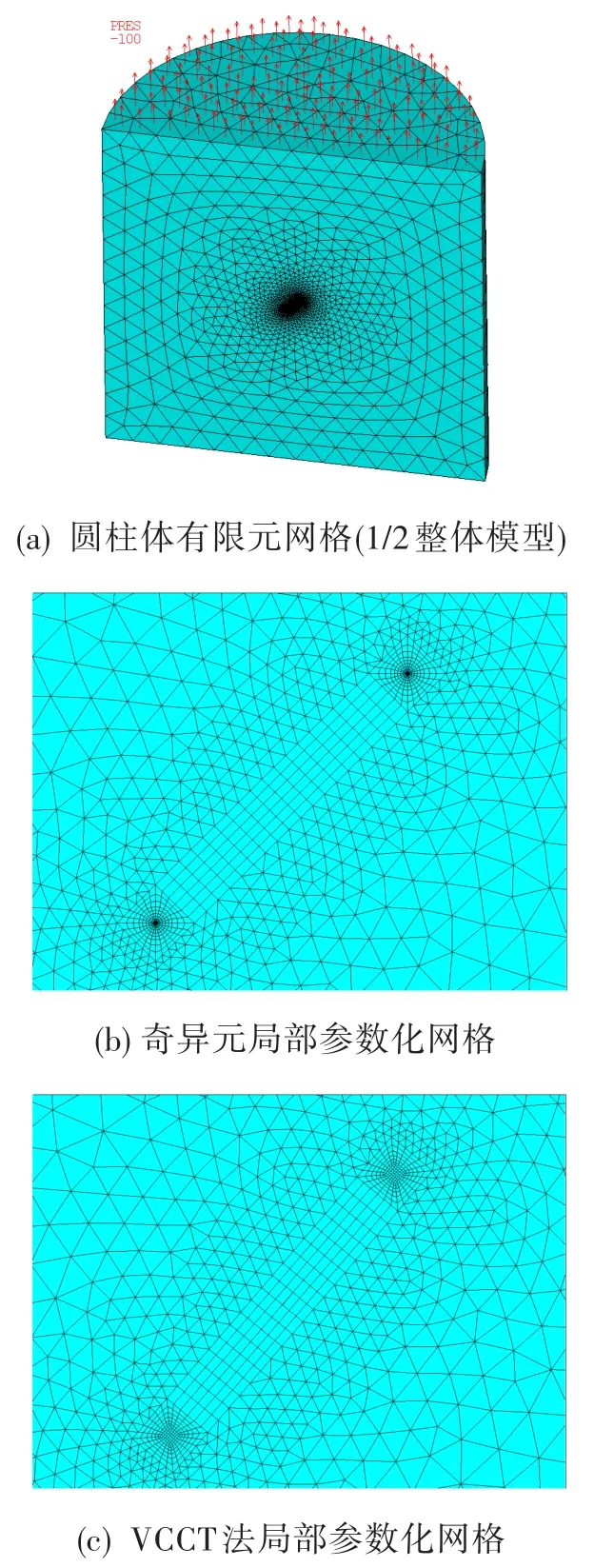
图9 有限元计算网格划分Fig.9 Computationalmesh generation using finite elementmethod

图10为奇异元法应力强度因子计算结果与解析解的比较。图中：KⅠ、KⅡ、KⅢ分别为Ⅰ、Ⅱ、Ⅲ型应力强度因子。可看出，其计算结果与解析解十分吻合。无论是Ⅰ型应力强度因子，还是其他两个分量(对应Ⅱ、Ⅲ型)，其结果与解析解的差别从图中已无法分辨。

图10 奇异元法计算结果与解析解的比较Fig.10 Comparison between FEM solution and theoretical result

对于Ⅰ型应力强度因子，奇异元法最大相对误差小于0.05%；对于Ⅱ型应力强度因子，其最大相对误差小于0.10%；对于Ⅲ型应力强度因子，其最大相对误差为0.51%(101个节点中，95个计算点相对误差小于0.10%，4个节点的相对误差在0.10%～0.51%之间，2个理论值为0)。

图11示出了VCCT法计算结果与解析解的相对误差。对于Ⅰ型应力强度因子，VCCT法最大相对误差介于0.20%～0.25%之间；对于Ⅱ型应力强度因子，其最大相对误差介于0.05%～0.15%之间；对于Ⅲ型应力强度因子，其最大相对误差介于0.15%～0.30%之间。

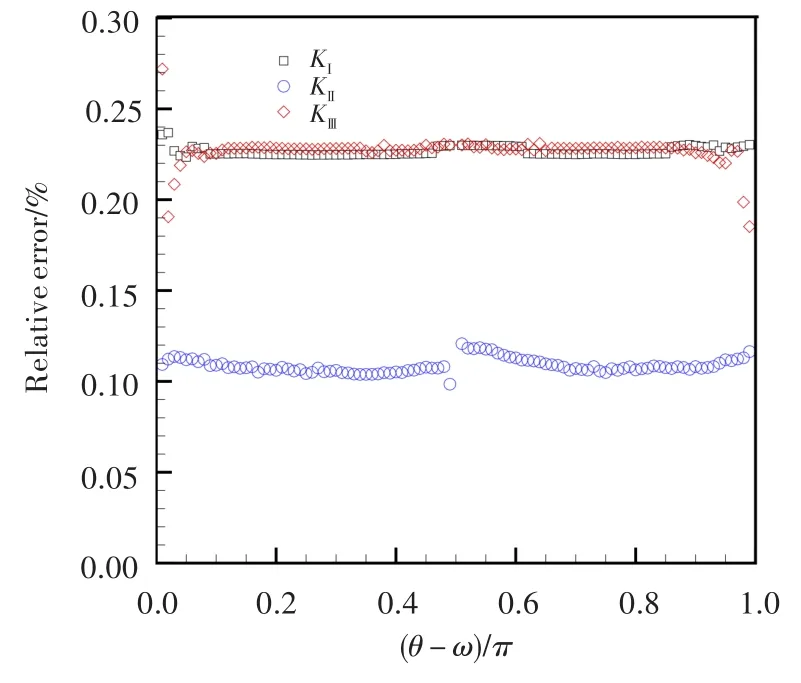
图11 VCCT法计算应力强度因子与解析解的相对误差Fig.11 Comparison between VCCT and theoretical resultbased on relative error of stress intensity factor

从计算结果与解析解的对比分析可以看出，无论是本文建立的奇异元法网格模型还是VCCT法网格模型，获得的应力强度因子精度都很高。虽然VCCT法平均误差略大，但其误差趋于均匀化，相对误差的分散性反而小于奇异单元法，显示出很好的数值稳定性。

4.2 涡轮叶片疲劳裂纹扩展算例

某涡轮叶片按前述方法建立的具有裂尖的计算网格如图12所示，在离心和气动力共同作用下涡轮叶片发生疲劳破坏。通过模拟分析该叶片疲劳破坏形貌，其结果与实际涡轮叶片疲劳裂纹扩展的对比如图13所示，可见其形貌吻合良好。

图12 涡轮叶片裂纹块计算网格Fig.12 Computationalmesh generation of the turbinewith the cracked block

图13 涡轮叶片裂纹扩展轨迹数值模拟结果与实际开裂形貌的对比Fig.13 Comparison between calculation and reality for crack shape developmentofa turbine blade

5 结论

基于参数化设计思想，分别开发了奇异元法和VCCT法对应的两种裂尖参数化网格模型。这两种模型首先通过实体分块，将裂尖附近划分出比较规则的实体模型，然后选择适当的参数进行网格细化，并通过编程实现裂纹体与无裂体网格的无缝对接，并保证裂纹前缘网格正交。算例验证表明，三维实体裂纹前缘参数化网格模型建模方法合理、可行，具有良好的计算精度。

[1]Schöllmann M，Fulland M，Richard H A.Development of a new software for adaptive crack growth simulations in 3D structures[J].Engineering Fracture Mechanics，2003，70 (2)：249—268.

[2]Zentech manufacturing-contractmanufacturing and engi⁃neering design services[EB/OL].http://www.zentech.com/.

[3]Cornell fracture group[EB/OL].http://www.cfg.cornell.edu/ index.htm.

[4]徐 杰.表面疲劳裂纹扩展的数值模拟[D].杭州：浙江理工大学，2012.

[5]唐俊星，陆 山.三维裂纹整体参数化模化方法[J].航空动力学报，2008，23(4)：737—741.

[6]于培师.含曲线裂纹结构的三维断裂与疲劳裂纹扩展模拟研究[D].南京：南京航空航天大学，2010.

[7]贾 旭，胡绪腾，宋迎东.基于三维裂纹尖端应力场的应力强度因子计算方法[J].航空动力学报，2016，31(6)：1417—1426.

[8]陈景杰，黄 一，刘 刚.基于奇异元计算分析裂纹尖端应力强度因子[J].中国造船，2009，51(3)：56—64.

[9]俞树荣，吴艳萍，荆 炀.表面裂纹的三维模型及应力强度因子计算[J].兰州理工大学学报，2017，43(1)：160—164.

[10]齐桂营.具有倾斜裂纹的CTS试样三维断裂行为的研究[D].哈尔滨：哈尔滨工程大学，2011.

[11]Lin X B，Smith R A.Finite elementmodeling of fatigue crack growth of surface cracked plates PartⅠ:The numerical tech⁃nique[J].Engng.FractureMech.，1999，63(5)：503—522.

[12]Lin X B，Smith R A.Finite element modeling of fatigue crack growth of surface cracked plates PartⅡ:Crack shape change[J].Engng.Fracture Mech.，1999，63(5)：523—540.

[13]Shivakumar K N，Tan P W，Newman J J.A virtual crack-closure technique for calculating stress intensity factors for cracked three dimensional bodies[J].Interna⁃tional Journalof Fracture，1988，36(1)：43—50.

[14]Rybicki E F，Kanninen M F.A finite element calculation of stress intensity factors by amodified crack closure integral [J].Engineering FractureMechanics，1977，(9)：931—938.

[15]樊 鸿，张 盛，王启智.复合型三维裂纹应力强度因子计算方法研究[J].四川大学学报，2009，41(4)：48—52.

[16]中国航空研究院.应力强度因子手册[M].北京：科学出版社，1993.

M esh param eterizationm odelsof three-dim ensional crack front

HOU Le-yi1，TANG Jun-xing2
(1.Nanjing Engineering Institute of AircraftSystems，Jincheng，AVIC，Nanjing 211106，China；2.Schoolof Power and Energy，Northwestern PolytechnicalUniversity，Xi’an 710072，China)

To realize the automatic 3D crack fatigue propagation simulation and obtain higher accuracy of stress intensity factor(SIF),on the basis of the parametric entitymodeling,two kinds of parametricmesh of near crack tip were developed,which corresponding to the singular elementmethod and virtual crack clo⁃sure technique(VCCT)to calculate the SIF,and both parametricmesh were interchangeable formutual au⁃thentication.Both crack models were carefully designed,using uniform transition orthogonal grid near the crack tip,and densitywas adjustable also along the crack front.Compared with analytical solution results,it shows that both kinds of parametric grid model have high calculation precision,thus can provide a techni⁃calsupport in achievingmore accurate resultof the SIF for a generalengineering structure.

three dimensional fatigue crack；crack propagation；virtual crack closure technique；

V231.9；O346.1

A

1672-2620(2017)03-0042-06

2017-04-11；

2017-05-12

侯乐毅(1977-)，男，山东潍坊人，高级工程师，主要从事辅助动力系统研究。