基于近似模型的变循环发动机稳态性能分析及优化

韩 佳，苏桂英，张跃学

(中国航发沈阳发动机研究所，沈阳110015)

基于近似模型的变循环发动机稳态性能分析及优化

韩 佳，苏桂英，张跃学

(中国航发沈阳发动机研究所，沈阳110015)

针对变循环发动机可调节变量多的特点，基于变循环发动机稳态性能计算结果，提出了通过构建和利用近似模型对稳态性能进行分析、优化的研究方法，同时还建立了优化求解程序。以超声速巡航工况稳态性能的分析及优化为例，解析了主要变几何部件调节对推力和耗油率的影响，获得了满足优化条件的性能方案。与传统大范围变几何部件参数研究方法对比验证表明，该方法在提高设计效率方面作用显著。为变循环发动机性能分析及控制规律设计提供了一种研究方法。

航空发动机；变循环；变几何部件；双外涵；性能优化；近似模型；响应曲面

1 引言

变循环发动机(VCE)能通过改变可变几何部件/机构的形状、尺寸或位置来改变发动机的热力循环参数，从而使发动机在各种工作条件下都具有优良的热力循环状态[1-3]。但由于变循环发动机可调部件的增加和参变量的增多，也导致其性能优化较常规涡扇发动机更为复杂[4]。因此，VCE的特性分析及性能优化对其研究具有重要的意义。

从上世纪50年代末60年代初VCE概念提出至今，美国从未间断对变循环技术的研究。同时，法国和日本也紧随美国的研究步伐开展了相关研究，积累了一定经验。国内对VCE的研究起步较晚、基础较薄，对其特性的认识也较浅。工程上，主要基于大范围的可调部件参数研究结果，根据约束条件进行筛选，观察分析变化规律，细化调节范围及步长、反复计算，最终得到工程上的最优方案。基础研究方面，朱之丽、王占学等开展了变几何部件调节对VCE性能影响的研究[5-7]，黄红超、刘振德等开展了基于Isight平台的发动机性能优化分析[8-9]，随阳等提出了基于遗传算法的VCE稳态性能优化方法[10]。但研究也发现：基于可调部件参数研究的优化方法，存在计算量大、设计效率低且无法考虑到空间内所有解的问题；基于遗传算法等的优化方法[11-12]，虽然能快速得到VCE稳态性能的优化结果，但却很难获取变几何部件调节对稳态性能的影响规律，不利于对VCE特性的研究。

为此，本文提出了基于近似模型的发动机性能分析及优化方法。以VCE超声速巡航状态为例，通过构建和求解近似模型，分析了变几何部件调节对发动机稳态性能的影响规律；同时建立优化程序，求出较优的性能方案，并与参数研究的寻优结果进行对比，以期为VCE的设计和性能优化提供帮助。

2 研究方案

以一双外涵VCE的设计方案为基础，对其超声速巡航性能进行分析、优化。首先根据典型工作状态，确定变几何部件寻优分析的调节范围；应用适当的虚拟试验设计方法确定样本方案点，并利用VCE稳态性能计算程序对样本方案点进行计算。随后根据样本方案点的计算结果，建立发动机性能参数及约束参数关于变几何部件调节参数的近似模型，利用近似模型对部件调节的耦合作用进行分析。最后根据方案优化设计中的约束条件，对近似模型直接求解，得到优选方案，指导VCE设计和研究。分析及优化流程如图1所示。

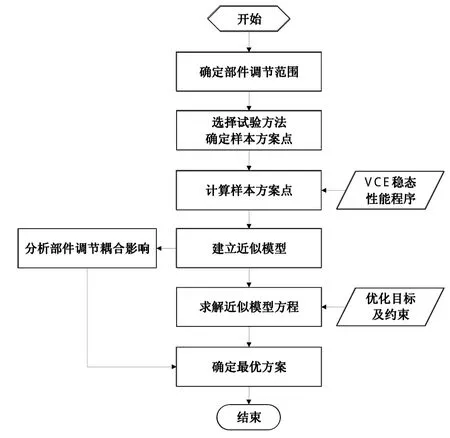
图1 基于近似模型的稳态性能分析及优化流程Fig.1 Analysisand optim ization processof VCE steady-state performance based on approximatemodels

3 近似模型的建立

超声速巡航时，要求发动机在不加力状态下工作。为获取足够的推力，在该状态点选用单外涵小涵道比模式。此时核心机驱动风扇(CDFS)导叶角度开大，同时低压涡轮导向器面积开大、后涵道引射器(RVABI)外涵面积及喷管喉部面积缩小。本文在方案分析时，CDFS导叶角度开至最大，在高/低压物理转速、涡轮前温度不超限的情况下，改变低压涡轮导向器面积、RVABI外涵面积及喷管喉部面积进行性能匹配，控制规律表达式见式(1)。

式中：n1为低压物理转速，n2为高压物理转速，T4为涡轮前温度，下标max表示最大限制值。

变几何部件参数调节范围见表1，表中 ALPT代表低压涡轮导向器面积，ARVABI代表后涵道引射器外涵面积，A8代表喷管喉部面积。为方便数据处理及分析，文中推力Fn、耗油率SFC均以相对变几何部件不调节方案性能变化百分比表示。

表1 变几何部件参数调节范围Table 1 Parameter adjustmentdomain of variablegeometry components

在变几何部件参数调节范围内，选取85个样本方案点，利用VCE稳态性能程序对样本方案点进行计算，并对计算结果进行二次响应曲面(RSM)[13]建模分析，建立寻优目标及限制参数的近似模型。

近似模型的复相关系数R2及修正的复相关系数AdjR2较高，表明模型具有高的响应度。图2给出了表1参数变化范围内，步长为单位1的所有点组合方案的近似模型计算值相对稳态性能程序计算值的误差分布。从图中可以看出：所建立的近似模型的误差在3%以内，且误差在-1%～1%之间的方案占总方案的百分比高于50%。这表明该近似模型误差较低，分布趋势近似正态分布，可以用于参数分析及性能优化。

4 基于近似模型的性能分析及优化结果

4.1 变几何部件联合调节对性能的影响

近似模型能反映变几何部件调节对总体性能影响的趋势。图3给出了任意两个变几何部件调节对超声速巡航状态推力及耗油率的影响，其中第三个参数设为取值范围内的中间值。

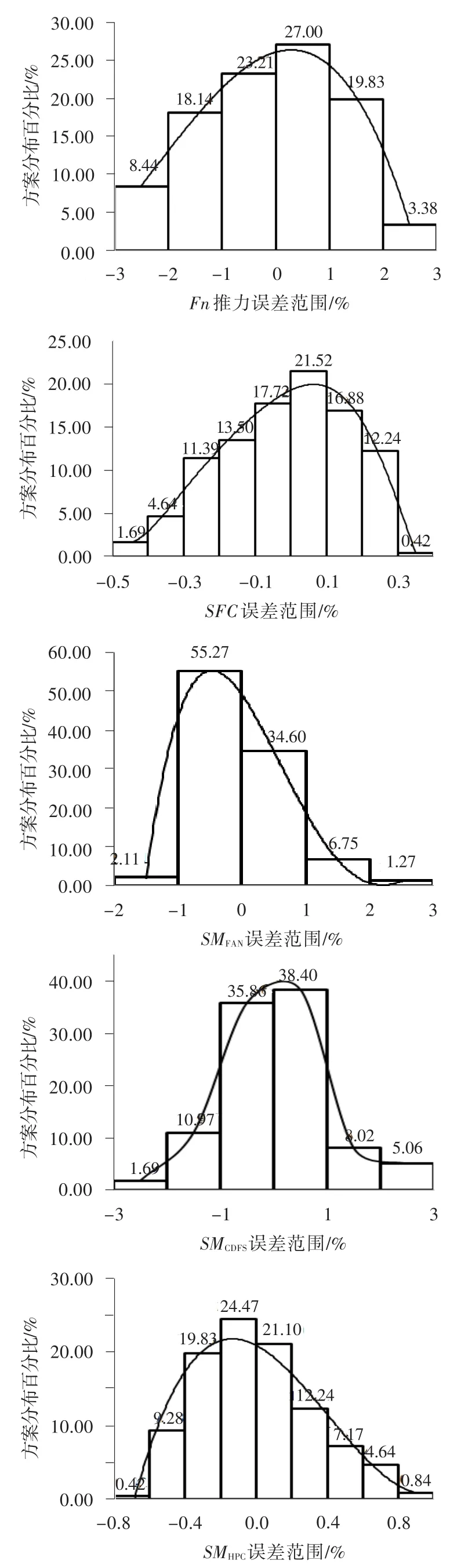
图2 近似模型的求解误差分布Fig.2 Solution error distribution ofapproximatemodels

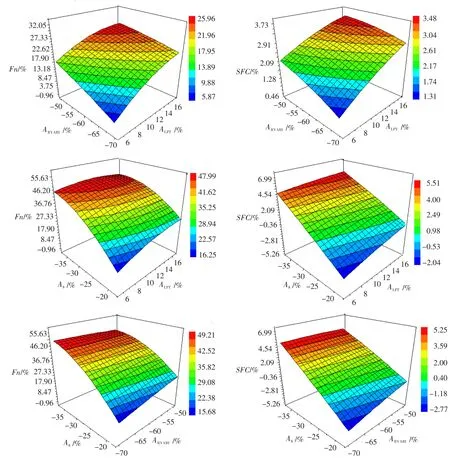
图3 任意两个变量对推力、耗油率的影响Fig.3 Effectofany two variableson Fn and SFC

分析图3可知，变几何部件调节对超声速巡航状态推力和耗油率的影响趋势基本一致；喷管喉部面积和低压涡轮导向器面积对性能的影响较大，而后涵道引射器外涵面积对性能的影响较小；各变几何部件调节对发动机性能存在耦合作用。喷管喉部面积和低压涡轮导向器面积匹配调节的耦合作用明显，下面就两者耦合作用对推力的影响进行详细分析。

随着喷管喉部面积的增加，低压涡轮膨胀比增大，涡轮做功能力增强，高、低压物理转速呈现增加的趋势，而低压物理转速先达到限制值。随着喷管喉部面积的进一步增加，低压涡轮膨胀比进一步增大，此时必须通过减小燃烧室供油量降低涡轮前温度，以保持低压物理转速不超出限制值，而此时高压物理转速开始减小，推力呈下降趋势。

随着低压涡轮导向器面积增加，高压涡轮膨胀比增大，高压涡轮功增加，高压物理转速增加，发动机涵道比降低，推力呈增加趋势。然而，高压物理转速达到限制值后，需要通过减小燃烧室供油量降低涡轮前温度，以保持高压物理转速不超出限制值，此时发动机推力呈降低趋势。

喷管喉部面积较大时，低压物理转速较高，甚至达到限制值。此时，高压物理转速较低，高压物理转速可增加的裕度较大。因此，随着低压涡轮导向器面积的增加，高压物理转速增大，推力增加。随着喷管喉部面积的减小，低压物理转速不再受限，涡轮前温度提高，高压物理转速增大。此时，高压物理转速可增加的裕度较小，随着低压涡轮导向器面积的增加，高压物理转速增加直到达到限制值。因此，推力呈先增加后下降的趋势。喷管喉部面积进一步减小，高压物理转速此时已达到限制值，随着低压涡轮导向器面积的增加，涡轮前温度降低，推力呈下降趋势。

4.2 稳态性能优化结果

不加力超声速巡航状态对发动机推力提出了较高的要求，同时还要求发动机具有较低的巡航耗油率。因此，在VCE方案设计阶段，选取在一定耗油率限制内使得推力最优的模式，对超声速巡航状态性能进行优化。

优化目标：Fn约束条件：

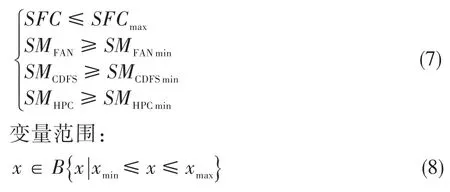
式中：x为变几何部件调节变量。

采用传统大范围参数研究的方法，选取的参数见表2。需计算1 573个方案点。经计算及筛选，得出超声速巡航状态工作点参数，见表3中传统方法的优化方案。根据所建立的近似模型及优化限制条件，对超声速巡航状态方案进行优化，得到变几何部件的最佳参数组合，并以VCE稳态性能程序对该参数组合进行验算，得出最终优化方案的推力及耗油率。优化方案1的优化目标是推力最大；优化方案2的优化目标是推力与传统方法优化结果相等，减小变几何部件调节量。优化结果见表3中基于近似模型的优化方案1和优化方案2。

表2 变几何部件参数研究范围Table 2 Parameter study range of variable geometry components

表3 传统方法和基于近似模型优化方法的优化结果Table 3 Optimization resultswith traditionalmethod and themethod based on approximatemodels

从表3中可以看出，在耗油率、压缩部件稳定裕度满足要求的条件下，优化方案1的无量纲推力较传统优化方法的推力高0.57个百分点，低压涡轮导向器面积调节量降低8.39个百分点，RVABI外涵面积调节量降低8.24个百分点；推力相当时，优化方案2的低压涡轮导向器面积调节量较传统优化方法降低8.73个百分点，RVABI外涵面积调节量降低10.46个百分点。由此可见，采用基于近似模型的优化方法，可以以更少的计算量得到更优的方案计算结果。

5 结论

以超声速巡航状态优化为例，验证了基于近似模型的变循环发动机优化方法的可行性及准确性。通过研究得出以下结论：

(1)超声速巡航状态，喷管喉部面积减小、低压涡轮导向器面积增大会造成推力和耗油率有增加的趋势，RVABI外涵面积对发动机性能的影响较小。

(2)相比常规涡扇发动机，变循环发动机性能模型的非线性、强耦合特点更加明显，变几何部件交互作用对性能的影响较大；随着低压涡轮导向器面积的增大，推力、耗油率增加，但这种趋势随着喷管喉部面积的减小而减弱，在喷管喉部面积小至一定程度后，推力甚至有降低趋势。

(3)基于近似模型的优化算法，一方面能够在保证发动机稳定裕度要求的前提下，匹配出较优的变几何部件调节方案，将变循环发动机的性能发挥得更优；另一方面能够在满足一定性能要求的前提下，匹配出变几何部件调节量更小的方案，降低变几何部件和控制系统的设计难度。

(4)本文的优化流程、方法同样适用于变循环发动机的其他飞行状态，有利于充分挖掘变循环发动机的性能优势，提高设计研究效率，为变循环发动机的特性研究及控制规律设计提供新思路、新方法。

[1]Vyvey P，Bosschaerts W，Villace V F，et al.Study of an airbreathing variable cycle engine[R].AIAA 2011-5758，2011.

[2]Johnson JE.Variable cycle engines-the next step in pro⁃pulsion evolution[R].AIAA-P-76-758，1976.

[3]方昌德.变循环发动机及其关键技术[J].国际航空，2004，(7)：49—51.

[4]朱之丽，王晓波.高推重比涡扇发动机性能寻优分析研究[J].航空动力学报，1999，14(7)：260—264.

[5]朱之丽，李 东.变几何涡扇发动机几何调节对性能的影响[J].航空动力学报，1999，14(1)：35—38.

[6]周 红，王占学，刘增文，等.双外涵变循环发动机可变几何特性研究[J].航空学报，2014，35(8)：2126—2135.

[7]刘增文，王占学，黄红超，等.变循环发动机性能数值模拟[J].航空动力学报，2010，25(6)：1310—1315.

[8]黄红超，王占学，刘增文，等.基于iSIGHT的变循环发动机性能优化[J].机械设计与制造，2012，(2)：217—219．

[9]刘振德，薛 亮，陈玉春，等.涡扇发动机性能优化调整的理论与试验研究[J].推进技术，2006，27(3)：211—215.

[10]随 阳，叶志锋，薛益春.基于遗传算法的变循环发动机稳态性能优化[J].航天控制，2013，31(6)：17—21.

[11]刘旭东，郭迎清.基于遗传算法的涡扇发动机最大状态性能寻优[J].航空计算技术，2006，36(6)：54—58.

[12]时瑞军，樊思齐.基于遗传算法的涡扇发动机多变量加速寻优控制[J].推进技术，2003，24(4)：357—360.

[13]薛 亮，韩万金.基于遗传算法与近似模型的全局气动优化方法[J].推进技术，2008，29(3)：360—366.

Analysisand optim ization of variab le cycle engine steady-state perform ance based on app roxim atem odels

HAN Jia，SUGui-ying，ZHANG Yue-xue
(AECCShenyang Engine Research Institute，Shenyang 110015，China)

Focus on features of variable cycle enginewhich hasmany variable geometry components,based on results of steady-state engine performance calculation as well,approximatemodelwas constructed and itsutilization on performance analysisand optimization was proposed as researchmethod.Optimization solv⁃er program was also established.Taking performance analysis and optimization of supersonic cruise condi⁃tion asexample,influence of themain variable geometry components on thrustand fuel consumption wasan⁃alyzed and performance scheme satisfying the optimization condition wasobtained.Compared with tradition⁃alwide-range variable geometry components parameters studymethod,this one shows significantmerits on improving design efficiency.Itprovides a researchmethod for the performance analysis of variable cycle en⁃gine and control law design.

aero-engine；variable cycle；variable geometry component；double bypass；performance optimization；approximatemodel；response surface

V231.3

A

1672-2620(2017)03-0016-05

2016-11-06；

2017-02-22

韩 佳(1987-)，男，黑龙江齐齐哈尔人，工程师，硕士，主要从事航空发动机总体性能设计工作。