“比例尺”教学中怎样引领学生思考
2017-07-24陈祖爱
文︳陈祖爱
“比例尺”教学中怎样引领学生思考
文︳陈祖爱
“比例尺”这一内容,是通过比例尺的意义和例题的教学,使学生理解比例尺的含义,学会求平面图的比例尺。本课的重点是让学生理解比例尺的意义,学会求比例尺,难点是多角度理解比例尺的含义。那么,教师在比例尺教学中如何增强学生的数学思考呢?
一、创设情境,激发学生思考
课始,我设计了一道脑筋急转弯题:“今天早上老师从家到学校上班用了15分钟,可是有一只蚂蚁从县城爬到长沙却只用了1分钟,这是为什么?”学生感到很奇怪,激发了学习兴趣。有学生想到:蚂蚁是在地图上走。教师顺势介绍图上距离和实际距离的概念,追问:“从县城到长沙的距离很长,为什么画出来却那么短呢?”学生说:“已经被缩小了!”教师很自然地揭示课题:“在生活中,我们经常要把一些物体按一定比例放大或缩小。这个统一的标准就叫做比例尺。看了这个课题,你想知道什么?”有学生说:“我想知道什么叫比例尺。”也有学生说:“我想知道比例尺有什么用。”由此,学生带着问题开始了新课的学习。
二、把握本质,探究引发思考
在教学比例尺的概念时,当学生理解了1∶100000000的含义后,教师指出,1∶100000000还可以写成分数形式,并介绍数值比例尺概念。接着,教师出示线段比例尺(图上的厘米代表实际的千米),问:“图上1厘米表示实际多长?”学生回答:“1厘米表示实际的50千米。”教师追问:“50千米就是多少厘米?”学生说:“5000000厘米。”教师顺势小结:“这两种比例表示的意义是相同的,都是图上距离与实际距离的比。”教师接着追问:“数值比例尺与线段比例尺,你更喜欢哪一个?为什么?”学生通过探究、比较,把握了线段比例尺的优势。
接着,教师用课件展示教材中的设计图纸,提问:“图中的2∶1表示什么?”学生说:“图上距离是实际距离的2倍。”教师追问:“这个比例尺跟刚才的比例尺有什么不同?”学生说:“刚才的比例尺前项是1,现在的比例尺后项是1。”教师追问:“为什么会这样?”学生说:“刚才是把物体缩小,现在是把物体放大。”教师顺势揭示放大比例尺的概念,并总结:不管是放大比例尺还是缩小比例尺,它们都有一项是1。为了计算方便,通常把比例尺写成前项或后项是1的比。在画图时,根据一定的比例尺,我们可以把物体放大或缩小。当然,也可以把物体按照原来大小画下来。
把放大、缩小和等比比例尺三种情况放在一起比较,学生理解了比例尺的本质属性。
三、拓展提升,问题激活思考
在完成基本练习后,教师补充拓展提高练习(课件出示):说出下面比例尺的实际意义。
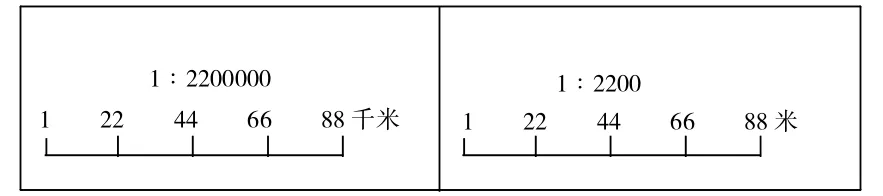
在学生说出比例尺的含义后,教师提问:“哪一幅图上的1厘米表示的实际距离长?理由是什么?”学生说:“第一幅图的1厘米表示22千米,第二幅图的1厘米表示22米。所以是第一幅图。”教师肯定了学生的想法,继续提问:“同样长的实际距离,画在哪一幅图上长呢?理由呢?”学生都认为是画在第二幅图上的线段长,并认为第二幅图的比例尺小。教师追问:“仔细想一想,是第二幅图的比例尺小吗?”学生沉思片刻后,说:“是第二幅图的比例尺的值大,缩小的比第一幅图少,所以画在第二幅图上的线段长。”教师小结:“同样长的实际距离,当比例尺的值大时,图上的距离长;当比例尺的值小时,图上的距离就短。”
这两个问题激活了学生的数学思考,让学生在思考中受益匪浅。
(作者单位:攸县莲塘坳中心小学)
