基于PMSM DTC的单位功率因数控制方法的研究

申 斌, 张晓宇

(华北科技学院 电子信息工程学院，北京 东燕郊 101601)

基于PMSM DTC的单位功率因数控制方法的研究

申 斌, 张晓宇

(华北科技学院 电子信息工程学院，北京 东燕郊 101601)

针对内置式永磁同步电机(IPMSM，Interior Permanent Magnet Synchronous Motor)，为充分利用逆变器的容量，提出了一种新型单位功率因数(cosφ=1)控制方法，无需进行复杂的坐标变换，实现起来更简单。在转子同步旋转坐标系下，对永磁同步电机的数学模型进行分析，推导得出单位功率因数控制的电磁转矩、定子电流以及电机转矩角的表达式，并详细阐明具体实现方法。同时采用SVPWM算法以减小转矩脉动，最后用MATLAB/Simulink软件搭建单位功率因数控制系统的仿真模型，仿真结果验证了该方法的有效性。

永磁同步电机；直接转矩控制；单位功率因数；SVPWM

0 引言

永磁同步电机的直接转矩控制是以定子磁场定向，直接把转矩作为被控量，通过选择合适的空间电压矢量来控制定子磁链的运动，最终达到控制电磁转矩的目的，具有结构简单、动态响应快等优点。对永磁同步电机直接转矩控制的研究，很多文献关注如何减小转矩脉动这一点上，如文献[1]提出运用空间矢量电压调制的方法以使逆变器开关频率恒定，从而减小转矩脉动；文献[2]提出一种改进的占空比调制方法来减小转矩脉动，都取得了一定成果。

已有文献中，详细研究单位功率因数控制的并不多见，文献[3]提出了一种基于永磁同步电机直接转矩控制的单位功率因数控制方法，但其中所用到的坐标变换比较复杂，本文的研究正是在文献[3]的基础上进行的，直接根据电磁转矩求出定子电流的交、直轴分量，从而使控制结构更加简单，容易实现。

1 永磁同步电机的数学模型分析

文中一律采用内置式永磁同步电机，电机在转子同步旋转坐标系下的矢量图如图1所示，图中α-β为两相静止坐标系，M-T为两相定子磁链同步旋转坐标系，其中M轴方向为定子磁链方向，d-q轴为两相转子磁链同步旋转坐标系，其中d轴方向与转子磁场方向重合。

图1 IPMSM坐标系和矢量图

定子磁链方程为

(1)

定子电压方程为

(2)

电磁转矩方程为

(3)

式中，Rs是定子电阻；ud、uq、id、iq、Ld、Lq、ψd、ψq分别是电压、电流、电感和定子磁链在d、q轴上的分量；ψs、ψf分别是定、转子磁链；ω是转子的电角速度；Te是电磁转矩；p是电机极对数；δ是定转子磁链之间的夹角，即转矩角；φ是定子端电压us与定子电流is之间的夹角，即功率因数角。

当采用id=0控制时，is方向与q轴重合，此时内功率因数角为零，转矩角与功率因数角相等，即δ=φ，电流、磁链、转矩、功率因数分别计算如下：

由此可得功率因数为

由转矩公式可见，采用id=0控制时，由于永磁体磁链大小不变，电磁转矩中只包含永磁转矩部分，而磁阻转矩部分为零，未充分发挥内置式永磁同步电机交直轴电感不等、磁阻转矩大的优点，正因为此，id=0控制多应用于表面式永磁同步电机[5]。从功率因数公式中可看出，功率因数随定子电流的增大而减小，而电磁转矩大小又与定子电流大小成正比，故当负载转矩加大时，定子电流增大，功率因数下降，这正是采用id=0控制时的劣势，而单位功率因数控制正好可以弥补这一不足[6-8]。

2 单位功率因数控制分析及系统实现

当采用单位功率因数控制时，功率因数恒为1，即定子端电压us与定子电流is重合，故is与q轴之间的夹角也等于转矩角δ。

由此可得出

(4)

把(4)式代入(3)式，可得

(5)

把(4)式代入(1)式，定子磁链变为

(6)

(7)

将(6)式代入(7)式，可得

Ldissin2δ+Lqiscos2δ-ψfsinδ=0

(8)

对(8)式变形为

(Lq-Ld)issin2δ+ψfsinδ-Lqis=0

求解可得单位功率因数控制的转矩角表达式

(9)

在(8)式两边同乘以is，并把(4)式代入其中，可得

(10)

将(10)式代入(3)式可得电磁转矩与定子电流直轴分量关系为

(11)

文献[3]中，在实现永磁同步电机的单位功率因数控制时，引入了P-Q同步旋转坐标系，把P轴作为有功功率轴，与定子电压矢量us方向相同，Q轴作为无功功率轴，与定子磁链矢量ψs方向相同。只需保证定子电流矢量is也与P轴重合，即可实现单位功率因数控制。但在求出功率因数角之后，仍需进行α-β坐标系到P-Q坐标系的变换，实现起来比较复杂。

本文中，模仿永磁同步电机直接转矩控制系统的最大转矩电流比控制[9]时，采用的已知电磁转矩求定子电流交、直轴分量的过程，提出一种新的单位功率因数控制方法，可省去从α-β坐标系到P-Q坐标系变换这一过程。图2为单位功率因数控制框图：

当传感器检测到的电机转速反馈值与给定转速值比较后，经过限幅PI调节器后，得到电磁转矩Te；将电磁转矩值代入(11)式中，即可求得定子电流直轴分量id的值，再将id的值代入(10)式，又可求得定子电流交轴分量iq的值，这一计算过程实际上就是图2框图中的cosφ=1控制部分，由此可见这种方法能够省去一次坐标变换。由于式(11)、(10)都比较复杂，为保证控制系统的实时性，本文采用曲线拟合的方法，具体可参见文献[9]。图3为仿真中采用的SVPWM模型。

图2 单位功率因数控制框图

图3 SVPWM仿真模型图

3 仿真分析

针对一台内置式永磁同步电机，利用Matlab/Simulink仿真软件首先对其建立单位功率因数控制系统的仿真模型，之后进行仿真分析，电机参数为：定子电阻为3.8 Ω，直轴电感为0.129 H，交轴电感为0.265 H，电机极对数为4，电机转动惯量为0.0006 kg·m2。设置仿真系统为固定步长(Fixed-step)仿真，步长为1e-5s，求解器采用ode4(Runge-Kutta)算法，仿真总时间为0.5 s。仿真中经试凑得到，转速调节器的PI参数设为Kp=1、Ki=12，交、直轴电流调节器的PI参数均为Kp=1.6、Ki=30。

仿真初始时刻，设定电机负载为空载，电机给定转速为500 r/min；0.15s时刻给电机加负载3 N·m，同时给定转速为1000 r/min；0.3 s时刻给电机加负载6 N·m，同时给定转速为1200 r/min。

永磁同步电机单位功率因数控制的电磁转矩波形如图3所示，从图3中可看出电机的输出转矩能准确跟踪给定转矩，在0.15 s时输出转矩迅速稳定在3 N·m附近，在0.3 s以后输出转矩稳定在6 N·m附近，且转矩脉动较小；图4为电机转速波形，从图4可看出，电机只有在刚启动0.05 s内，转速有一微小波动，0.05 s之后能严格跟随给定转速，在0.15 s和0.35 s时刻，当给定转速改变时，电机输出转速能在瞬间改变，这说明所采用的控制方法保留了直接转矩控制动态性能好的优点。

图3 电磁转矩波形

图4 转速波形

图5为定子三相电流波形，图6为定子A相电流波形，从图中可看出，在电机启动瞬间有较大的冲击电流，但持续时间很短暂。当电机输出转矩增大时，对应的定子电流也相应增大。

图5 定子三相电流波形

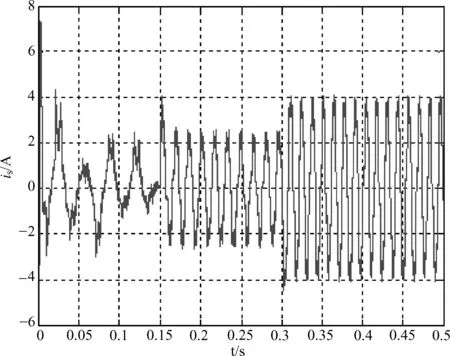
图6 定子A相电流波形

4 结论

本文对内置式永磁同步电机的单位功率因数(cosφ=1)控制方法进行了研究，文中采用的方法无须用到复杂的坐标变换，实现起来更为简单。同时，可以在一定程度上减小定子电流幅值，进而可以降低电机损耗，提高电机运行效率，提高对逆变器容量的利用率。仿真结果验证了，所采用的单位功率因数控制方法完全保留了传统DTC的优良性能，能够实现系统控制的快速性和准确性，具有一定的工程意义。

[1] 孙丹，贺益康. 基于恒定开关频率空间矢量调制的永磁同步电机直接转矩控制[J].中国电机工程学报，2005，25(12):112-116.

[2] 孙德明,杜明星,刘志宏,等.一种改进的永磁同步电机直接转矩控制方法[J].电机与控制应用,2017,44(2):47-52.

[3] 刘文良,张国政. 永磁同步电机单位功率因数控制[J].微电机,2012,45(2)：63-67.

[4] 唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社，2016.

[5] 樊明迪.永磁同步电机直接转矩控制技术研究[D]. 西安:西北工业大学，2014.

[6] 盛义发,喻寿益.新型 PMSM 直接转矩控制方法[J].电气传动，2009，39(3)：14-17.

[7] 唐校，杨向宇，赵世伟,等.非恒定磁链幅值给定的永磁同步电机直接转矩控制[J].电力自动化设备,2015,35(9)：37-42.

[8] 杨建飞,胡育文.永磁同步电机最优直接转矩控制[J].中国电机工程学报,2011,31(27)：109-115.

[9] 曹晖,罗峰,周盼,等.永磁同步电机最大转矩电流比控制的仿真研究[J].微电机,2015,48(6)：55-59.

Research on Unity Power Factor Control Based on PMSM-DTC

SHEN Bin, ZHANG Xiao-yu

(NorthChinaInstituteofScienceandTechnology,Yanjiao, 101601,China)

Based on the interior permanent magnet synchronous motor, a new unity power control method is proposed in order to make full use of the inverter capacity, which is easier to implement without complex coordinate transformation. In the rotor coordinate system which rotates synchronously, the mathematical model of permanent magnet synchronous motor is analyzed. The electromagnetic torque, stator current and the torque angle of the unity power factor control are derived and realized. And the algorithm of SVPWM is used to reduce the torque ripple. Finally, the simulation model of the unity power factor control is built in the Simulink of Matlab and the simulation results show the feasibility of the method.

PMSM; Direct Torque Control(DTC); Unity Power Factor; SVPWM

2017-01-12

国家自然科学基金(61304024)；河北省科技计划项目(15272118)；中央高校基本科研业务费资助项目(3142015143、3142016022)

申斌(1988-)，男，河南郑州人,华北科技学院在读硕士研究生。E-mail：18730652940@163.com

TM351

A

1672-7169(2017)02-0097-05