长短桩复合地基沉降计算方法分析及探讨

张昌进，张 勇

(华北科技学院，北京 东燕郊 101601)

长短桩复合地基沉降计算方法分析及探讨

张昌进，张 勇

(华北科技学院，北京 东燕郊 101601)

地基沉降计算在地基基础工程中存在着很大的难题。虽然许多研究在沉降计算方面付出了巨大的努力,但在计算精度上仍存在很大差异。现行的关于长短桩复合地基沉降理论一直处于摸索和发展之中。本文通过对等效天然地基法和加权模量法进行沉降计算，分析得出：(1)等效天然地基计算计算结果比较符合实际，加权模量法计算虽然比较简单，但是沉降计算的误差比较大。(2)加权模量法沉降计算中，桩体对褥垫层及下卧层都具有一定的刺入变形。针对刚性长短桩体在复合地基中的压缩模量计算没有考虑桩顶和桩底的刺入变形效应。而在实际工程中，仅由桩身压缩模量计算得到的复合模量和实际有很大误差，因而计算得到长短桩复合地基的沉降量很小，不符合实际需要，故本文提出一种方法对加权模量法计算方法进行改进，希望其有助于复合地基沉降计算的深入研究。

长短桩复合地基；等效天然地基法；加权模量法

长短桩复合地基[1-3]一般是采用短桩加固浅层软土，提高其承载力和压缩模量，减少沉降; 而长桩则考虑应力扩散的关系，上部荷载通过桩身向深层传递，控制沉降。复合地基沉降是值得研究的重要问题之一，但由于复杂性，沉降规律仍处于发展之中。加固层的沉降主要由桩体和天然土所形成的复合土的变形构成。下卧层土层由于加固区存在,使其压缩增加。由于长短桩复合地基变形分析理论不完善，所以目前的沉降计算大多采用经验公式。一般来说，沉降量分为三个部分，即长短桩共同加固区沉降量、长桩单桩加固区沉降量及下卧层沉降量。其研究主要集中在加固区的复合模量计算方法[4-6]。加固区的复合模量计算方法用于工程设计的主要有等效天然地基法和加权模量法。

1 等效天然地基法

1.1 复合模量计算

复合地基中桩体的存在可以大大提高天然地基的承载特性和控制沉降变形量，复合模量的计算也是沉降计算的关键之处。在实际工程中，桩的变形模量的确定是困难的。考虑桩土应力比和桩土模量相关性，土的模量[7-8]可以表示为弹性模量，，通过分析比较图桩体模量以及土体模量的相互作用性，可以反映其桩土的作用关系，从而提高桩体和土体参数的准确性，减小误差。长短桩复合地基的复合模量确定如下：

(1) 将长短桩复合地基视为天然地基。加固土层压缩提高系数为ζ1，根据每个土层的压缩模量所得，ζ1可按照下式计算：

ζ1=fspk/fak

fak—天然地基承载力特征值，kPa；

fspk—长短桩复合地基承载力特征值，kPa。

(2) 计算了等效天然地基法以及短桩复合地基的复合模量，即长短桩复合地基的复合模量。将短桩桩长范围内各个土层的模量均乘以ζ2得到加固区后各土层的模量。ζ2可以按下式计算：

ζ2=fspk1/fspk

fspk1—长桩单独加固复合地基承载力特征值，kPa；

fspk—长短桩复合地基承载力特征值，kPa；

2 加权模量法

复合地基沉降计算的关键在于分析土中附加应力的分布及复合地基复合模量的计算。在了解长短桩复合地基的受力变形机理后，再来讨论其复合模量的确定方法。

在复合模量法中，桩土复合模量通常采用面积加权法计算，在复合地基中假设桩土共同作用时变形协调，按照材料力学方法，由桩土变形协调条件推导出面积加权公式。

长短桩共同加固区复合模量：

Esp1=m1Ep1+m2Ep2+(1-m1-m2)Es

长桩单独加固区复合模量：

Esp2=m1Ep1+(1-m1)Es

式中，Ep1、Ep2、Es分别为长桩、短桩和桩间土压缩模量,m1、m2分别为长桩和短桩的面积置换率。

该方法简单，并且具有一定的精度。但其假设过于理想，不能反映复合土的变形特性，因而存在一定的缺陷。对于中、高粘结强度桩，如果两桩复合地基材料相同而桩长不同，土压缩模量Es相同。较高的复合模量相同桩在相同的条件下，桩端落在软、硬层的复合模量是不一样的，但根据上面的公式计算是一样的，体现不出最终的效果。

3 工程实例沉降计算

3.1 工程概况

拟建天洋城三期工程地点位于燕郊开发区亿丰大街南侧、汉王路西侧。场地所处地貌类型为第四纪河流冲击平原地貌。剪力墙结构，筏板基础，埋置深度7 m。经地质勘查，基础持力层以3层粉质粘土为主。由于基底以下存在较厚的杂填土，天然地基不能满足要求。经对桩基和复合地基的分析，地基采用CFG桩和素混凝土夯扩桩组合的复合地基处理形式。基础底面尺寸长90 m，宽14 m。CFG桩有效桩长29 m，直径为450 mm，共295根，正三角形布桩，桩间距为1.5 m。夯扩桩共295根，有效桩长为8 m，直径为500 mm。两类桩体材料采用碎石、中粗砂，按体积比2 ∶1人工拌和，碎石最大粒径小于30 mm。各土层参数见下表1所示。

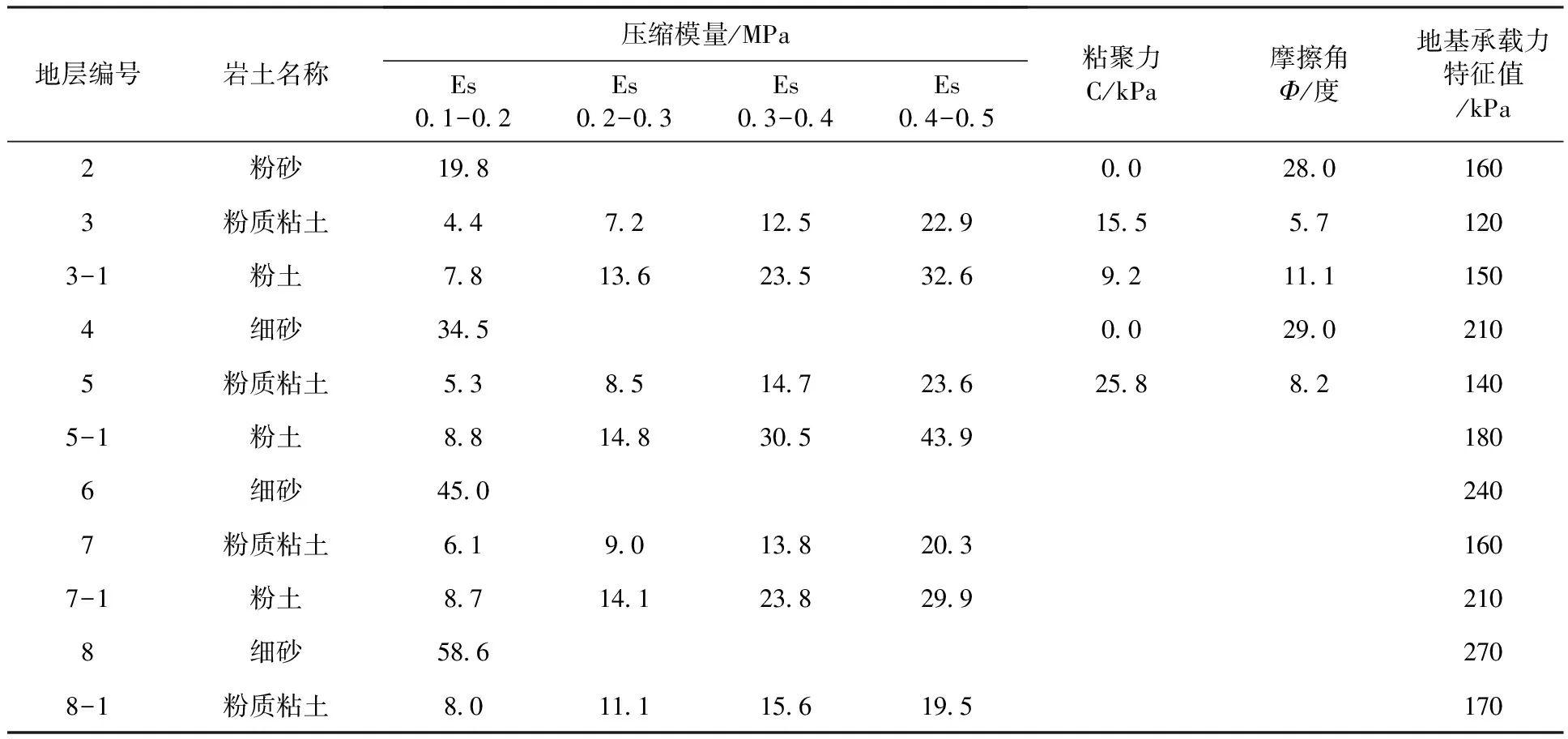
表1 土层主要物理参数

3.2 等效天然地基法沉降计算

根据布桩情况可知，长桩和短桩的面积置换率分别为0.018和0.022，截面积分别为0.159 m2和0.196 m2。基础底面附加应力为305.4 kPa。

加固区承载力特征值：

=281.754(kPa)

式中β—桩间土发挥系数，结合工程经验取值0.95.

取沉降计算经验系数ψs=0.25，计算过程如图表2所示，所得沉降量为：

长短桩共同加固区沉降量：

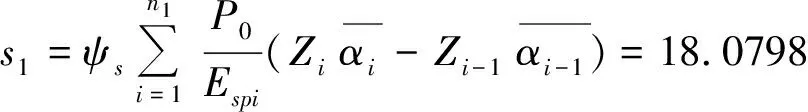
长桩加固区沉降量：

下卧层沉降量：

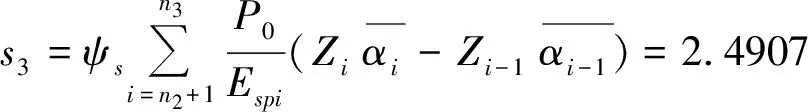
计算结果表明，总沉降量为33.9 mm。沉降主要发生在加固区，加固区沉降占总沉降的比值为92.64%。下卧层沉降量不大。

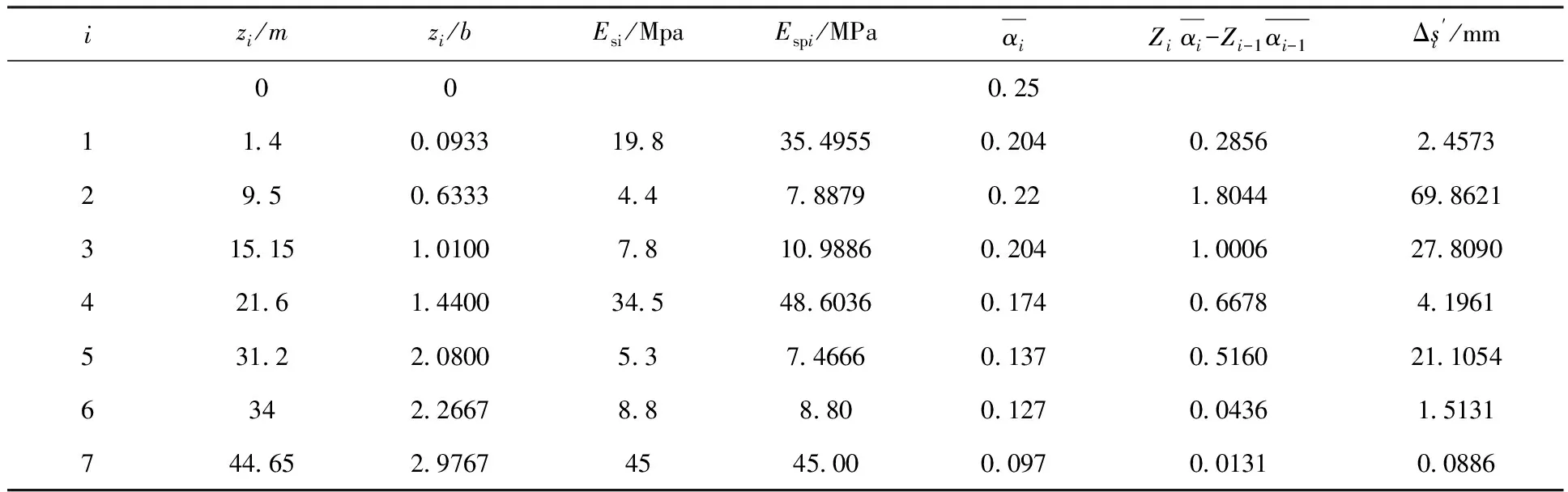
表2 等效天然地基法地基沉降量计算

续表

3.3 加权模量法沉降计算

在本工程中，长桩和短桩的压缩模量分别为30000 MPa和17500 MPa，面积置换率分别为0.018 m2和0.022 m2，沉降计算经验系数为0.25。其计算过程如下表3所示，各部分沉降量分别为：

长短桩共同加固区沉降量：

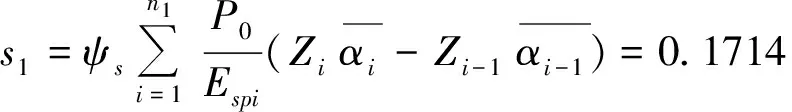
长桩加固区沉降量：

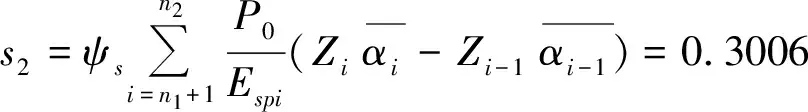
下卧层沉降量：

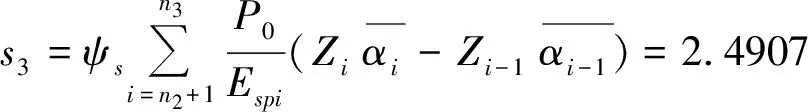
计算结果表明，总沉降量为3.0 mm，加固区的沉降量较小，加固区沉降占总沉降的比值为15.93%，而下卧层沉降量较大。

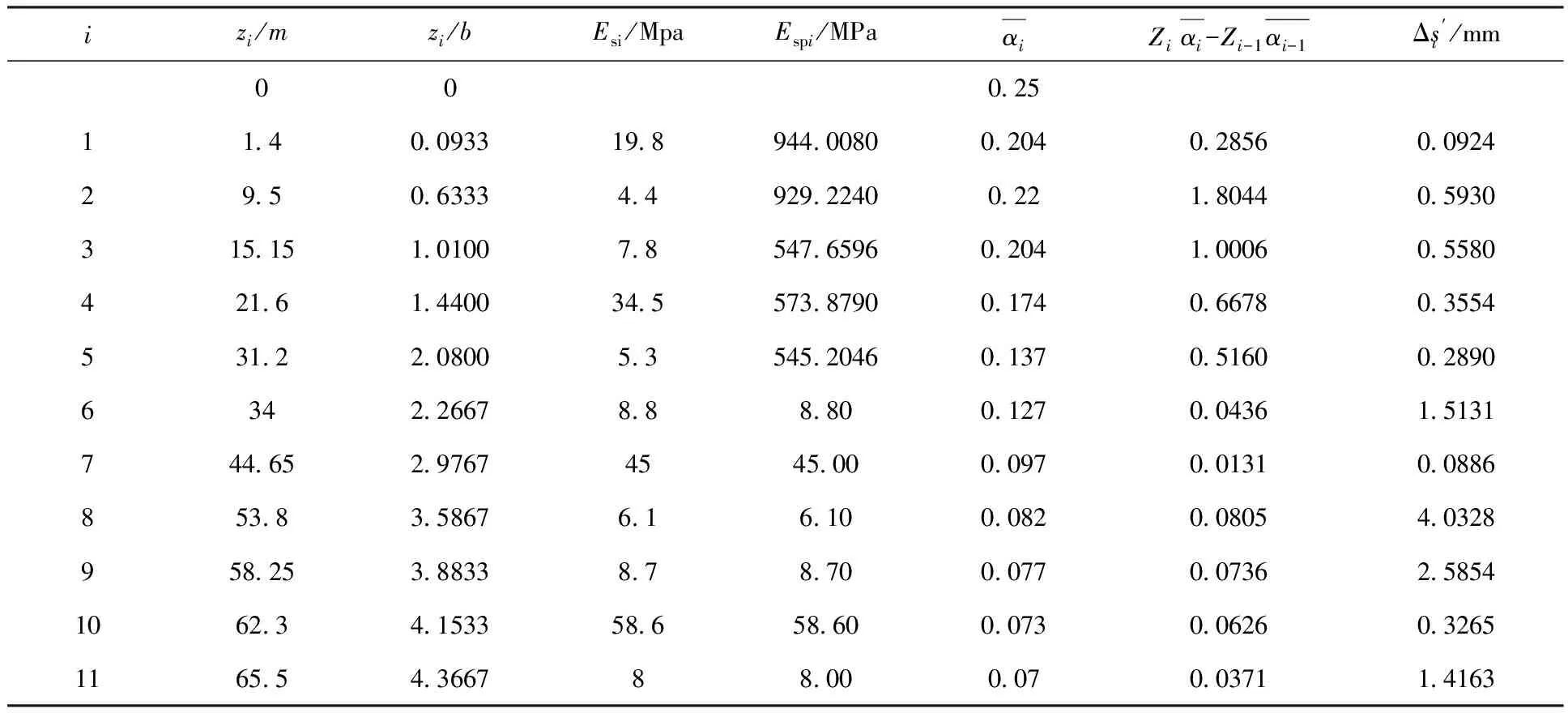
表3 加权模量法地基沉降量计算

3.5 计算与实测结果对比分析

从对比中可以看出，等效天然地基法得出总沉降量为33.9 mm。沉降主要发生在加固区，加固区沉降占总沉降的比值为92.64%。下卧层沉降量不大。采用加权模量法得出总沉降量为3.0 mm，

表4 沉降计算结果

加固区的沉降量较小，加固区沉降占总沉降的比值为15.93%，而下卧层沉降量较大。这与等效天然地基法得出的结果不同。虽然加权模量法计算比较简单，但是沉降计算的误差比较大，而等效天然地基法计算结果比较符合实际。

4 讨论

加权模量法的适用于散体桩或柔度较大的桩，并没有考虑桩长效应和桩端阻力效应。针对刚性长短桩体在复合地基中，桩体对褥垫层及下卧层都具有一定的刺入变形。而在实际工程中，桩体的压缩模量是由桩身模量和土层模量共同决定的。造成仅由桩身压缩模量计算得到的复合模量和实际有很大误差，因而计算得到长短桩复合地基的沉降量很小，不符合实际需要。

在实际工程中，由于存在桩顶和桩底的刺入变形，桩身应变εp远小于桩间土应变εs，加权模量法计算与实际情况相比误差较大，计算沉降量往往偏小。针对刚性长短桩复合地基加固区的复合模量过于放大，用桩体材料的压缩模量计算复合模量不能准确反应桩体的实际作用，应引入一个参数μ表示模量发挥系数即:

式中:n表示桩土应力比。故加权模量法改进后的长短桩复合地基各部分压缩的复合模量为：

Esp=μ1m1Ep1+μ2m2Ep2+(1-m1-m2)Es

Esp2=μ1m1Ep1+(1-m1)Es

由于其受力的复杂性及众多影响因素，对于长短桩复合地基的变形计算影响因素比较复杂，对桩顶和桩底的刺入变形计算和土层压缩模量需要考虑各种因素，故本文提出一种思路方法进行

加权模量法计算方法的改进，希望针对其复合地基沉降计算有助于深入研究。

5 结论

(1) 等效天然地基计算计算结果比较符合实际，加权模量法计算虽然比较简单，但是沉降计算的误差比较大。

(2) 加权模量法沉降计算中，桩体对褥垫层及下卧层都具有一定的刺入变形。针对刚性长短桩在复合地基中的压缩模量计算没有考虑桩顶和桩底的刺入变形效应。而在实际工程中，仅由桩身计算得到的压缩模量和实际有很大误差，因而计算得到长短桩复合地基的沉降量很小，不符合实际需要，提出一种改进的思路和方法。

[1] 桩基工程手册编写委员会.桩基工程手册[M].北京：中国建筑工业出版社,1997.

[2] 中华人民共和国国家标准编写组.GB5007-2011建筑地基处理技术规范[S].北京：中国建筑工业出版社，2012.

[3] 龚晓南.复合地基设计和施工指南[M].人民交通出版社,2003.

[4] 阎明礼,张东刚.CFG桩复合地基技术及工程实践[M].中国水利水电出版社，2001.

[5] 刘海涛,谢新宇,程功，等.刚-柔性桩复合地基试验研究[J].岩土力学,2005,26(2):303-306.

[6] 李锋利.长短桩组合桩基础室内模型试验分析研究[D].上海：同济大学,2006.

[7] 陆华,高全臣,吴浩，等.长短组合桩复合地基沉降预测研究[J].施工技术，2013,42(19)：30-36.

[8] 潘烈.填方路基下长短桩复合地基的沉降特性研究[D].西安:西安建筑科技大学，2012.

Analysis and Discussion on Settlement Calculation Method of Long and Short Pile Composite Foundation

ZHANG Chang-jin，ZHANG Yong

(NorthChinaInstituteofScienceandTechnology,Yanjiao,101601,China)

The foundation settlement calculation is a great problem in the foundation engineering. Although many studies have made great efforts in settling calculations, there are still significant differences in computational accuracy. The existing theory of composite foundation settlement for long and short pile has been in the process of groping and developing. In this paper, the equivalent natural foundation method and the weighted modulus method are used to calculate the settlement.The results show that (1) The calculation results of the equivalent natural foundation are realistic, and the calculation of the weighted modulus method is simple, but the error of its settlement calculation is larger.(2) In the settlement calculation of the weighted modulus method, the pile has a certain piercing deformation on the mattress layer and the layer under the floor. The calculation of the compressive modulus of the rigid long and short pile in the composite foundation does not take into account the piercing deformation effect of the pile top and the pile bottom. In the actual engineering, the composite modulus calculated by the compressive modulus of the pile only has a great error. Therefore, it is calculated that the settlement of the composite foundation is very small and does not meet the actual needs. Therefore, this paper proposes a method that improves weighted modulus method, and it is hoped that it can help to the deep study on the calculation of composite foundation settlement.

long and short pile composite foundation; equivalent natural foundation method; weighted modulus method

2017-03-25

中央高校基本科研业务费资助(3142015145,3142015136)

张昌进(1990-)，男，山东泰安人，华北科技学院在读硕士研究生。E-mail：1057995126@qq.com

TU473.1

A

1672-7169(2017)02-0044-05