基于复合抗饱和策略的火星飞机自适应控制

韩少君 倪 昆 熊寸平 张庆振

1.北京航空航天大学，北京 100191 2.北京航天自动控制研究所, 北京 100854

基于复合抗饱和策略的火星飞机自适应控制

韩少君1倪 昆1熊寸平2张庆振1

1.北京航空航天大学，北京 100191 2.北京航天自动控制研究所, 北京 100854

目前，伴随着火星探测的兴起，火星飞机越来越受重视。目前对火星大气研究不充分，火星飞机飞行环境特殊，存在强烈的不确定性和干扰。同时稀薄的火星大气与受限的飞机尺寸限制了操纵的机构控制能力。为了解决这2个关键问题，提出了一种基于复合抗饱和策略的自适应控制器，将模型误差、不确定性和干扰视为系统的“总和扰动”，利用扩张状态观测器观测并加以补偿。针对控制能力受限带来的控制饱和，提出伪控制限制与基于误差补偿的扩张状态观测器抗饱和方案相结合的复合抗饱和策略。仿真结果表明，该控制方法能较好地完成指令跟踪，并有效抵制不确定性和干扰影响，效果良好，有效改善了控制饱和带来的响应迟滞等现象，使系统具有较强的抗饱和特性。 关键词 火星飞机；扩张状态观测器；伪控制限制；复合抗饱和策略

近年来，对于火星飞机作为火星探测科学平台的讨论不断。传统轨道探测器属于大尺度探测，探测范围广，但探测颗粒度较大；火星探测器探测颗粒度较小，但属于小尺度探测，活动范围小。火星飞机则属于中尺度探测[1]，具有比天基平台轨道探测更高的分辨率及比火星表面探测器更大的活动范围，还具有比其他科学平台更高的操纵性。但是，火星飞机控制系统设计中面临几大突出问题：控制受限、强干扰和不确定性。

目前国内外对火星飞机控制问题有一些研究，主要采用H∞控制、复合非线性反馈控制的方法来设计火星飞机的控制系统[2-3]，这些文献中的控制器大都是基于理想情况设计的。实际上，由于火星表面大气稀薄、环境复杂， 火星飞机巡航飞行时，飞行跨度过大，或遇到外界干扰使飞行器的状态发生突变，执行机构容易饱和。当执行机构饱和后，飞行控制系统的控制性能将下降，甚至不稳定。对于自适应控制系统，执行器的长期饱和将带来严重不利的影响。因此，为了保证控制系统的性能，本文引入伪控制限制(Pseudo-ControlHedging,PCH)[4]及基于误差补偿的扩张状态观测器(ExtendedStateObserver,ESO)抗饱和方案[5]这2种机理不同但互补的抗饱和方案形成复合抗饱和策略，将其与控制系统结合，形成具有强鲁棒性与抗饱和特性的控制系统。

本文从火星飞机的纵向模型出发，考虑巡航飞行控制要求与参数不确定性，对模型进行反馈线性化处理，继而搭建基于扩张状态观测器的自适应控制系统，并且加入了复合抗饱和策略。给出了火星飞机模型、控制系统的结构与相关的数值仿真结果，验证了本文提出方法的有效性和优越性。

1 火星飞机模型

研究模型是火星飞机模型，由于火星大气稀薄，

假定火星飞机横纵向耦合较弱，建立纵向模型

(1)

其中，V,γ,h,α,q,β分别为速度、航迹倾斜角、高度、攻角、俯仰角速度和发动机节流阀；L,D,T,Myy分别为升力、阻力、推力和俯仰力矩，具体计算公式见文献[2]。

为了研究火星飞机巡航飞行控制，气动数据是在标称巡航段拟合简化而得，以文献[2]的气动数据为基准，加入拉偏项如下

(2)

火星环境数据及火星飞机模型数据获取自文献[6]，加入拉偏项如下

(3)

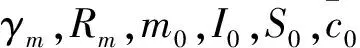
2 基于ESO的自适应控制器设计

2.1 输入/输出线性化

反馈线性化的基本思想是通过状态反馈消去非线性系统中的非线性部分，使闭环动态成为一个线性系统。输入/输出线性化是反馈线性化的一种，目的是建立系统输出与控制输入之间的一个简单而直接的关系。对于MIMO系统，每一个输出对时间求足够次数的微分，直至结果出现至少一个控制量为止，并记微分次数为ri。对于m维输出向量的n阶非线性系统，其相对阶r定义为

(4)

若r=n，则该系统能完全反馈线性化，没有零动态。在设计控制器时，不需要检验内动态是否稳定[7]。

对于巡航飞行控制，输出是火星飞机的速度V和高度h，输入为节流阀设置βc和升降舵偏角δe。对速度和高度分别连续求3次和4次微分，可以得到线性输出动态，则相对阶r为7。考察式(4)，系统阶数n为7。由于r=n，系统能完全反馈线性化，具体推导参见文献[8]，结果如下所示

(5)

2.2 控制器设计

式(5)写成紧凑形式

(6)

其中，f=[fV,fh]T,u=[βc,δe]T。

u=B-1(v-f)

(7)

根据式(7)设计非线性动态逆控制器

(8)

其中，

(9)

(10)

式(9)和(10)对应Vd,V,hd,h的各阶导数均由跟踪微分器生成。

结合上述式子，可以得到闭环系统的误差动态

(11)

式(11)对应的特征方程为

(12)

根据飞行任务要求，调整上述特征方程的系数至符合Hurwitz判据，能使速度、高度的误差动态渐进稳定到0。

2.3 扩张状态观测器(ESO)设计

火星飞机飞行过程中呈现很强的非线性特性，难以用解析式描述，导致动态逆控制器的控制性能降低。为了对系统的不确定性进行补偿，引入扩张状态观测器。ESO是自抗扰控制的核心，它能对系统的总扰动进行动态观测并在控制器中进行自适应补偿，且ESO的构建不依赖于生成扰动的具体数学模型，十分实用[9]。

在式(6)中加入火星飞机模型的不确定性及外界扰动，并将其等效至速度及高度通道，得

(13)

其中，[gV,gh]T为等效扰动，在此假定执行机构没有饱和情况出现，存在执行器饱和的情况将在后面详细介绍。

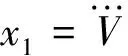
(14)

对式(14)系统设计二阶ESO

(15)

其中，非线性函数

g(z)=fal(z,α,δ)

(16)

根据文献[10]中“参数动态确定法”选取合适的α,δ,β01,β02，扩张状态观测器在保证自身渐近稳定性的同时，可以对等效扰动进行很好的估计，高度回路ESO的设计基本相同。

在对等效扰动[gV,gh]T进行了准确的估计之后，对2.2节中设计的动态逆控制器加入对扰动的抑制，可以实现对指令信号更好的跟踪，控制律为

(17)

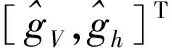
(18)

可以看出，只要ESO观测结果准确，等效扰动就可以得到很好的补偿，速度和高度得以准确地跟踪指令信号。

3 复合抗饱和策略

3.1 伪控制限制

(19)

将伪控制补偿信号引入参考模型中，改变参考模型的状态更新，进一步影响参考模型输出，从而将执行机构的饱和特性影响转移到参考模型中[4]。

伪控制限制结构如图1所示。

图1 伪控制限制结构

对于速度的参考模型，由于控制器的输入需要速度的3次微分，因此选择4阶的跟踪微分器，微分方程如下：

u=Vc

(20)

(21)

(22)

其中，

(23)

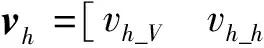
该跟踪微分器输出y的前3个分量，用于计算跟踪误差，即：

(24)

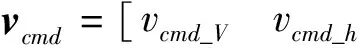
vcmd_V=x4

(25)

同理，对于高度的参考模型，选择5阶的跟踪微分器，微分方程及参考模型的输出如下：

u=hc

(26)

(27)

(28)

该跟踪微分器输出y的前4个分量，用于计算跟踪误差，即

(29)

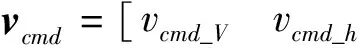
vcmd_h=x5

(30)

以速度通道为例，假设控制指令过大，执行机构饱和，则产生对应的伪控制补偿信号：

vh_V>0

(31)

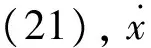
分析来自La Esperanza地区调查的数据。首先，参与超市供应链的概率被评估为社会经济，农业，交易成本和组织变量的函数。这一分析结果表明，社会经济和农业特点无统计显著性差异。这一结果的原因可能是调查人口的同质化，主要包括条件相似的小规模农户。然而，交易成本与生产低质量风险，运输和分级问题这些因素有非常重要的相关性，构成了农民在超市供应链中的参与约束。相反，供应链中相对较高的价格和对买家的信任，对农民加入又有积极的作用。有关交易成本的结果与本研究分析框架中的理论预期是一致的。

综上，伪控制限制抗饱和策略将执行机构输入动态对自适应控制器的影响转化为对参考模型的影响，从而避免扩张状态观测器受执行机构输入饱和的影响而输出错误的补偿信号。因此，引入伪控制限制抗饱和策略能保证扩张状态观测器估计补偿作用的正常运行，使自适应控制系统具有一定的抗饱和特性。

3.2 基于误差补偿的ESO抗饱和策略

执行机构饱和使控制器输出与执行器输出之间存在误差，导致控制器状态无法准确估计。ESO具有估计执行机构状态的功能，因此，可以将控制器输出与执行器输出之间的误差反馈回ESO，这样ESO就可估计并补偿执行机构饱和所带来的误差，实现抗饱和效果。同样，饱和约束环节前后的信号一致，补偿环节将不再发挥作用，系统转换为一般的自适应控制系统。

这种基于误差补偿的ESO抗饱和机构如图 2所示。

图2 基于误差补偿的ESO抗饱和方案

图2中，kc为可调节的误差补偿系数，增加kc可以使误差得到更快的补偿，但是会造成ESO的不稳定，因此kc需要调节至合适的值[5]。

以速度通道为例，扩张状态观测器经过抗饱和环节之后由式(15)成为

(32)

此时，由于控制饱和所造成的误差可以借助ESO的估计能力得到估计和补偿。

3.3 复合抗饱和策略与控制系统的结合

实际控制系统中，执行机构由于自身特性的限制，输出值不能准确地跟踪控制器输出，导致系统动态性能变差,甚至崩溃。执行机构约束造成控制器输出与执行器输出之间存在误差，抗饱和策略的实现正是基于这个误差。

由3.1节可知，伪控制限制抗饱和策略将控制器输出与执行器输出之间的误差称为伪控制补偿信号，通过输入输出线性化后的模型求解转化为参考模型补偿信号，将其引入参考模型生成环节中，通过减缓参考模型信号达到抗饱和的作用，从而保证扩张状态观测器的正常工作。

3.2节中基于误差补偿的扩张状态观测器抗饱和方案同样是基于控制器输出与执行器输出之间误差进行工作的。将该误差引入ESO中，利用ESO自身的估计补偿作用对其进行估计并补偿。通过改变ESO输出前馈补偿量调节控制器输出来达到抗饱和效果。

因此，伪控制限制与基于误差补偿的扩张状态观测器抗饱和方案同是基于控制器输出与执行器输出之间误差进行工作，伪控制限制抗饱和策略通过调节参考模型信号保证扩张状态观测器的正常工作，扩张状态观测器通过对该误差进行估计补偿，调节执行器输入达到抗饱和的效果。两者相辅相成、协同运作，成为一种复合抗饱和策略，与控制系统结合可以有效提高系统的抗饱和性能。

完整的控制系统如图3所示。

4 仿真结果及分析

初始条件：标称巡航段(V=150m/s,h=2500m)的配平状态，如下所示：

V=150m/s,γ=0rad,α=0.0281rad,

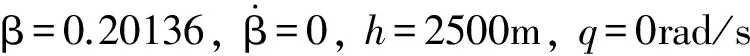
图3 复合抗饱和策略与控制系统结合

对于升降舵，传递函数为二阶惯性环节(ξ=0.707,ωn=25)，舵面偏转角最大范围为±20°，偏转速率最大范围为±60(°)/s。对于发动机节流阀，工作范围为[0,1]。

仿真指令：Vd=220m/s,hd=2700m的阶跃信号；ESO参数：α=0.5,δ=0.05,β01=100,β02=500；ESO误差补偿系数:kc_ βc=0.5,kc_δe= 0.9。

控制系统参数：λ1=0.8,λ2=1,

设定如下拉偏量：

无参数拉偏、加入扩张状态观测器、不加入抗饱和策略时，仿真结果如图 4所示，由于执行机构的持续饱和，ESO输出错误的补偿信号，导致高度和速度回路全都发散，最终导致系统崩溃。

在以上仿真基础上加入复合抗饱和策略，仿真结果如图 5所示，高度和速度准确跟踪参考模型输出。

图4 标称情况无抗饱和策略仿真结果

控制量仿真曲线如图 6所示，可以看出发动机节流阀在0～38s内一直处于幅值饱和状态，而升降舵在0～3s内处于速率饱和状态。扩张状态观测器结构中,由于饱和误差存在产生误差补偿量，对应于控制量饱和时段，基于误差补偿的扩张状态观测器抗饱和策略一直工作到执行机构饱和结束，由于执行机构饱和情况不太严重，仅有这一种抗饱和策略在工作，伪控制限制抗饱和策略没有产生作用，输出为0。

在参数拉偏、加入复合抗饱和策略时，仿真结果如图 7所示。由仿真结果可见，在执行机构饱和情况下，复合抗饱和策略同时作用,有效地消除执行机构饱和所带来的误差，高度和速度准确跟踪参考模型输出。

由图8可见，执行机构饱和时，伪控制限制环节有输出，从而影响参考模型的输出，减弱执行机构饱和影响。同时，ESO中误差补偿环节也在作用，通过ESO的估计补偿作用补偿消除部分执行机构饱和所带来的误差，通过复合抗饱和策略的应用，最终使系统跟踪误差无静差镇定到0，使系统具有较强的抗饱和特性。

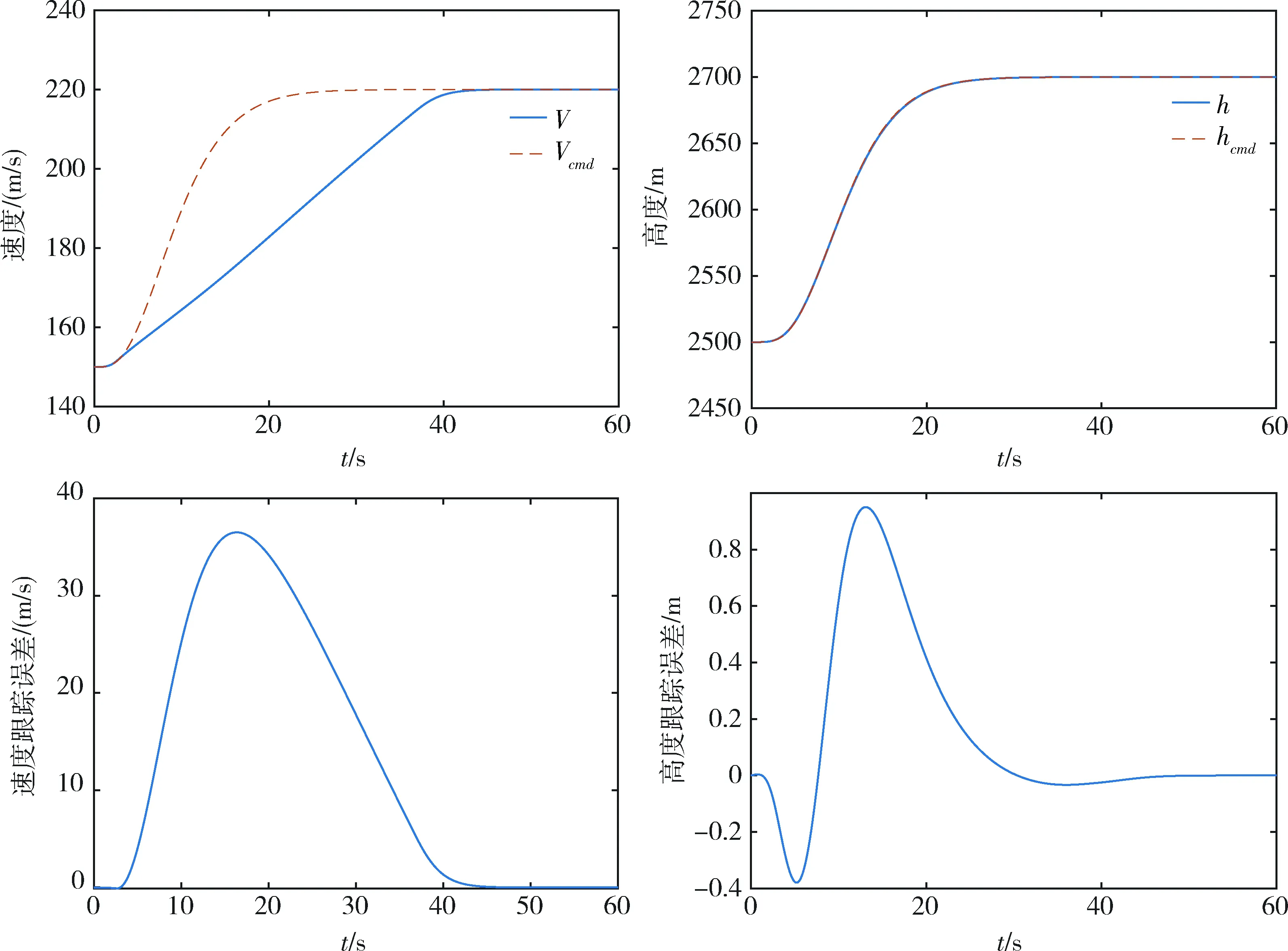
图5 标称情况应用复合抗饱和策略速度及高度跟踪曲线

图6 标称情况应用复合抗饱和策略控制量曲线

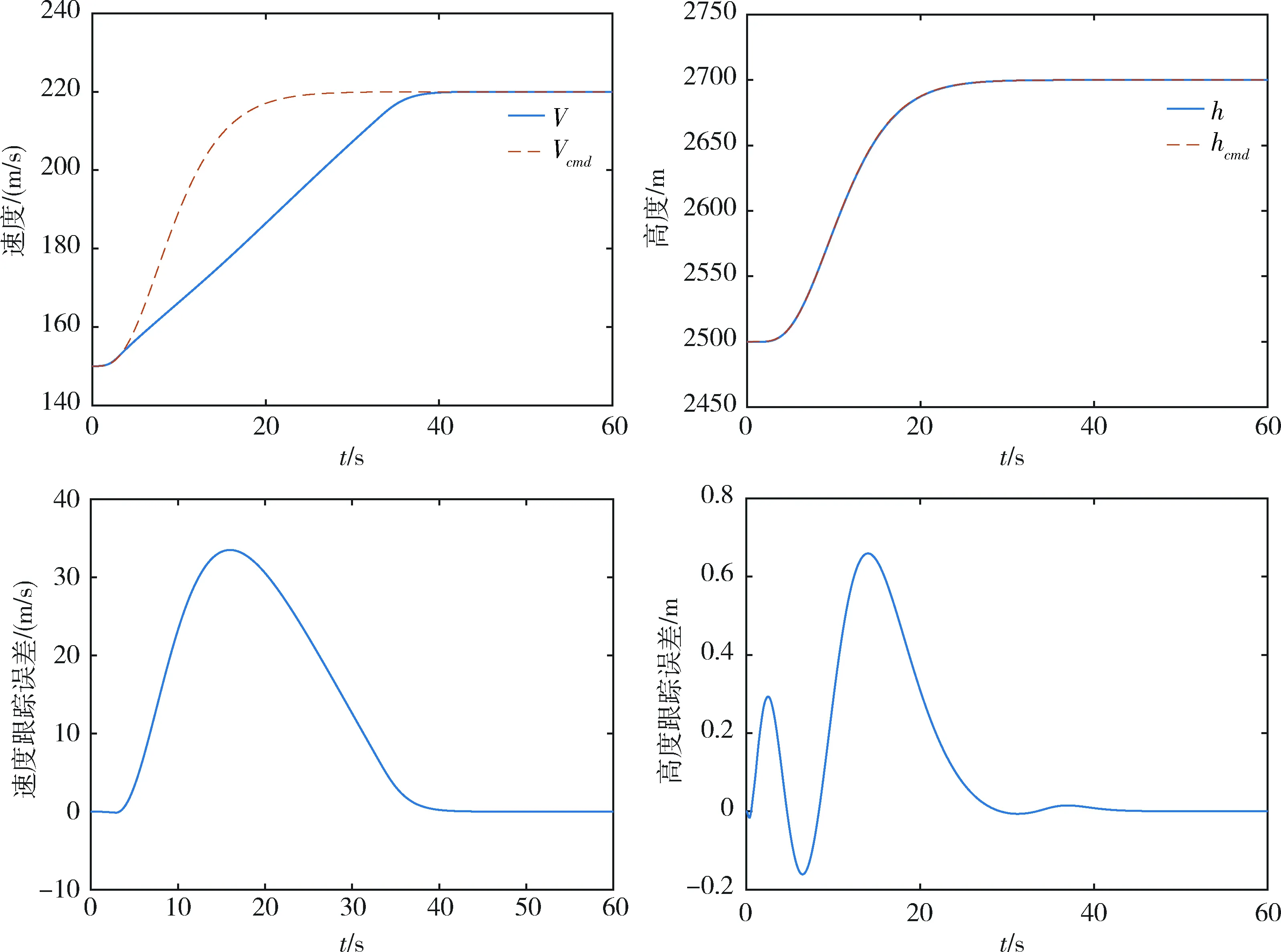
图7 拉偏情况应用复合抗饱和策略速度及高度跟踪曲线

图8 拉偏情况应用复合抗饱和策略控制量曲线

5 结论

研究了火星飞机巡航飞行控制问题，针对参数不确定性和输入饱和，设计了基于复合抗饱和策略的自适应控制器。利用扩张状态观测器良好的估计补偿能力，在没有或短时间的输入饱和情况下，扩张状态观测器能很好地消除模型误差，使系统的跟踪误差无静差镇定。同时，控制系统采用复合抗饱和策略,通过伪控制限制调节参考模型输出以及通过ESO估计补偿执行机构饱和带来的误差，避免长时间的输入饱和导致系统崩溃，使系统能够克服一定程度的输入受限问题。仿真结果表明，所设计的基于复合抗饱和策略的自适应控制系统具有较强的稳定性、鲁棒性和抗饱和特性。

[1]GuynnM,CroomM,SmithS,etal.EvolutionofaMarsAirplaneConceptfortheARESMarsScoutMission[C]//2ndAIAA"UnmannedUnlimited"Conf.andWorkshop&Exhibit. 2003: 6578.

[2]LiuY,PengK,LuY,etal.FlightControlLawUsingCompositeNonlinearFeedbackTechniqueforaMarsAirplane[J].JournalofGuidance,Control,andDynamics, 2016: 2199-2204.

[3]BhattacharyaR,ValasekJ,SinghB,etal.OnModelingandRobustControlofARES[C]//AIAAGuidance,NavigationandControlConferenceandExhibit. 2008: 7454.

[4] 轩慧娉, 贾晓洪, 马建伟, 刘忠. 基于伪控制隔离器的导弹控制方法研究[J]. 弹箭与制导学报, 2010, 30(5): 17-19.(XuanHuiping,JiaXiaohong,MaJianwei,LiuZhong.AdaptiveControlUsingPseudoControlHedgingforMissileCompoundControlSystem[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2010, 30(5): 17-19.)

[5] 周宏, 谭文. 线性自抗扰控制的抗饱和补偿措施[J]. 控制理论与应用, 2014, 31(11):1457-1463.(ZhouHong,TanWen.Anti-windupSchemesforLinearActiveDisturbanceRejectionControl[J].ControlTheory&Applications, 2014, 31(11): 1457-1463.)

[6]HjartarsonA,PawY,ChakrabortyA.ModelingandControlDesignfortheARESAircraft,Model-basedAerospaceChallenge# 1[C]//AIAAGuidance,NavigationandControlConferenceandExhibit. 2008: 7452.

[7]IsidoriA.NonlinearControlSystems[M].SpringerScience&BusinessMedia, 2013.

[8] Xu H, Mirmirani M D, Ioannou P A. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838.

[9] Han J. From PID to Active Disturbance Rejection Control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.

[10] 康忠健, 陈学允. 非线性扩张状态观测器的一种设计方法[J]. 电机与控制学报, 2001, 5(3): 199-203.(Kang Zhongjian, Chen Xueyun. A Design Method of Nonlinear Extension State Observer [J]. Electric Machines and Control, 2001, 5(3): 199-203.)

[11] 韩京清, 王伟. 非线性跟踪一微分器[J]. 系统科学与数学, 1994, 14(2): 177-183.(Han Jingqing, Wang Wei. Nonlinear Traclong-differeentiator[J]. Journal of Systems Science and Mathematical Sciences, 1994, 14(2): 177-183.)

Adaptive Control of Mars Aircraft Based on Compound Anti-Saturation Strategy

Han Shaojun1，Ni Kun1，Xiong Cunping2，Zhang Qingzhen1

1.Beijing University of Aeronautics and Astronautics, Beijing 100191, China 2. Beijing Aerospace Automatic Control Institute, Beijing 100854, China

Atpresent,withtherisingofMarsexploration, Marsaircraftisfocusedincreasingly.DuetothelackofatmosphericresearchonMarsandspecialflyingenvironmentoftheMarsaircraft,therearealsostronguncertaintyandinterference.ThecontrolofthecontrolmechanismisdeterminedbythethinMarsatmosphereandthelimitedsizeoftheaircraft.Inordertosolvethesetwokeyproblems,anadaptivecontrollerbasedoncompoundanti-saturationstrategyisproposed.Themodelerrors,uncertaintiesanddisturbancesareconsideredassumdisturbancesofthesystem,whichareobservedandcompensatedbyusingtheextendedstateobserver.Aimingatthecontrolsaturationcausedbythelimitationofcontrolability,acompoundanti-saturationstrategywhichiscombiningpseudo-controlhedgingwithanti-saturationschemebasedonextendedstateobserverisproposed.Thesimulationresultsshowthattheinstructioncanbetrackedandtheinfluenceofuncertaintyandinterferencecanberesistedeffectivelybyusingtheproposedcontrolmethod.Thecompoundanti-saturationstrategyhasgoodeffectandcanimprovetheresponsehysteresiscausedbythecontrolsaturation.Thus,thesystemhasastronganti-saturationcharacteristics.

Marsaircraft;Extendedstateobserver(ESO);Pseudo-controlhedging(PCH)；Compoundanti-saturationstrategy

2017-03-06

韩少君(1993-)，男，山西原平人，硕士，主要研究方向为导航、制导与控制；倪 昆(1991-)，男，苏州人，博士，主要研究方向为导航制导与控制；熊寸平(1979-)，男，浙江长兴人，硕士，主要研究方向为自动控制；张庆振(1976-)，男，江苏沛县人，博士后，主要研究方向为导航、制导与控制。

TP273

A

1006-3242(2017)03-0040-09