输入受限高超声速飞行器指数收敛状态反馈控制
2017-07-21关英姿
关英姿 朱 凯
1. 哈尔滨工业大学航天学院,哈尔滨 150001 2. 北京空天技术研究所,北京 100074
输入受限高超声速飞行器指数收敛状态反馈控制
关英姿1朱 凯2
1. 哈尔滨工业大学航天学院,哈尔滨 150001 2. 北京空天技术研究所,北京 100074

对具有不确定性的高超声速飞行器在输入受限情况下的稳定控制问题,基于线性矩阵不等式(LMI)技术提出了一种具有指数收敛速率的控制器设计方法。将飞行器模型中的不确定性视为总和扰动,针对存在不确定性的输入受限系统给出了一种具有指数收敛速度的不变集条件,并利用LMI技术将控制器的设计问题转化为受限系统吸引域的最优化问题。仿真结果表明,在气动参数摄动和控制量存在饱和的情况下,本文设计的指数收敛控制器具有良好的动态特性和鲁棒性。 关键词 高超声速飞行器;输入受限;不确定性;线性矩阵不等式;指数收敛
高超声速飞行器跨大马赫数、大空域飞行,其气动参数存在较大不确定性,且外界力、热环境较为严酷。因此,在对高超声速飞行器建模过程中不可避免地要考虑不确定性的影响。同时,高超声速飞行器飞行环境复杂,突风干扰会引起气动攻角的瞬态变化,进而造成明显的气动力矩变化,并且在超燃冲压发动机点火、级间分离等时刻,飞行器可能需要承受较为明显的外部扰动。这些瞬时力矩变化容易引起执行机构饱和,使控制系统不能实现预期的反馈控制,导致控制系统的动态性能降低,甚至会破坏控制系统的稳定性。
目前的文献中,针对高超声速飞行器的姿态控制问题,采用的控制方法主要有自适应控制[1-2]、反馈线性化控制[3]、模型预测控制[4]、滑膜控制[5]和增益调度控制[6],这些控制方法不同程度地解决了高超声速飞行器姿态控制中模型的强非线性和不确定性问题。
近年来,飞行器姿态控制中的输入受限问题也引起了广泛关注[6-10]。文献[6]针对具有不确定性的输入受限飞行器模型,研究了鲁棒变增益控制算法。针对BTT导弹的输入受限问题,文献[7]提出了一种二阶滑模自适应反演控制来解决姿态控制系统的输入受限和不确定性问题。针对控制受限的挠性航天器姿态控制问题,文献[8]给出了一种自适应滑模控制方法,显式地考虑了控制的饱和特性,证明了控制受限情况下系统的稳定性。文献[9]针对近空间飞行器这一类存在外部干扰、输入饱和以及参数不确定的多输入多输出线性系统, 提出了一种基于干扰观测器的抗饱和控制方法,保证了闭环系统的稳定性。尽管国内外学者针对姿态控制中的输入受限问题和模型的不确定性问题进行了大量研究,给出了一些有效的控制方法,但是这些研究中几乎没有特别关注系统的动态特性问题。
在解决控制系统的输入受限问题中,线性矩阵不等式(Linear Matrix Inequalities,简称LMI)作为一种有效的数学工具被广泛地应用于抗饱和补偿器以及状态反馈控制器的设计[11-19]。文献[11]利用LMI技术给出了一种抗饱和控制器的综合设计方法。文献[12]研究了输入受限系统的L2增益特性及稳定区域。文献[16]推导了输入受限系统在受扰情况下的不变集条件,研究了输入受限系统的抗干扰问题,但文中没有考虑系统轨迹的收敛速度和收敛时间,在受到干扰时无法保证控制系统具有满意的超调量和振荡次数等动态性能。
针对飞行器的输入受限和不确定性问题,本文将系统中的不确定性视为总和扰动,并针对输入受限受扰系统提出了一种具有收敛速度因子的不变集条件,将控制器的设计问题转化为不变集的最优化问题。
1 问题描述
飞行器的纵向运动方程为:
α=ϑ-θ
(1)
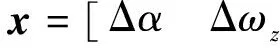
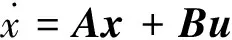
(2)

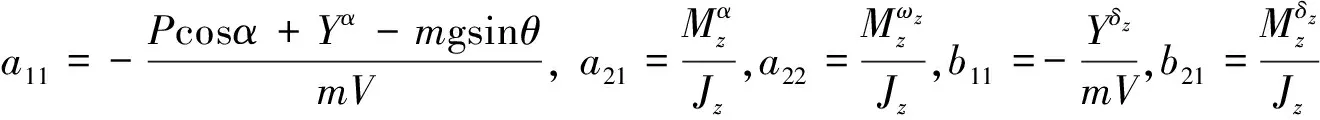
考虑系统式(2)中,舵偏角范围受到如下约束:
-ua≤u≤ua
(3)
式中,ua>0表示输入幅值约束的上限。
为了便于推导式(2)表示的输入受限系统的不变集条件,通过对式(2)中的B矩阵进行处理,得到式(4)表示的输入受单位约束的系统模型:
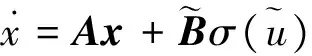
(4)
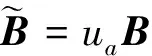
式(4)给出的飞行器纵向姿态模型中未考虑气动参数摄动、外界干扰以及线性化处理所带来的误差等不确定性。
将飞行器模型中存在的各种不确定性作为总和扰动进行考虑,则输入幅值受限系统的状态方程为:
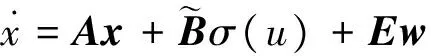
(5)
其中,w为干扰。
假设系统所受干扰能量有界,且满足:
wTw≤χ
(6)
其中,χ为已知正数。
对于存在输入受限以及能量有界不确定性的系统(5),采用常用的状态反馈形式控制律来保证系统的闭环稳定性,即:
u=Fx
(7)
式中,F∈Rm×n。
在式(7)所示控制律的作用下,系统的闭环形式可描述为:
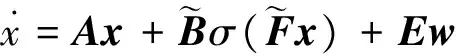
(8)
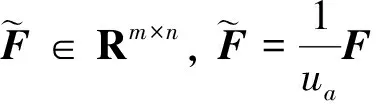
本文针对式(8)描述的幅值受限系统设计状态反馈控制器,使输入受限系统在状态反馈控制律的作用下,在受到有界扰动时仍能获得一个满意的收敛区域,且在该收敛区域内系统轨迹以一定速度渐进收敛到原点,在保证系统稳定性的同时获得良好的动态特性。
2 输入受限系统指数收敛控制器设计
当动力学模型中存在干扰时,系统的运动轨迹受到干扰的影响而发生变化,不变集条件与干扰的能量大小有关。本文综合考虑系统的不确定性和动态特性,针对不确定性系统给出了一种具有指数收敛性能的不变集条件。在此基础上,针对输入受限系统(5)的控制器设计问题,将不变集的最大化问题转化为具有LMI约束的凸优化问题,以最大收敛域为优化目标,通过求解最优问题,获得幅值受限系统的状态反馈控制律。
2.1 不确定系统的指数收敛不变集条件
吸引域、收缩不变集和线性区域的定义如下:
定义1 从初始状态x(0)=x0出发的系统轨迹为ψ(t,x0),关于原点的吸引域定义为:
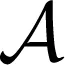
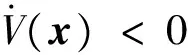
显然,若椭圆Ω(P,ρ)为收缩不变集,则椭圆Ω(P,ρ)位于吸引域内,饱和系统的吸引域可以通过不变椭圆进行近似。
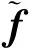
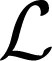
定义如下辅助矩阵[7]:

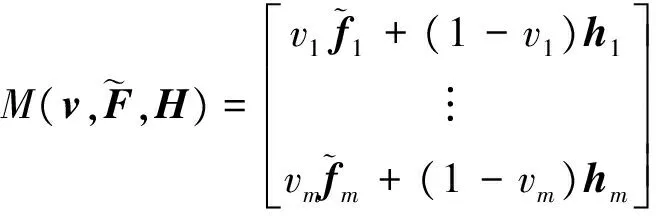
在不变集条件的推导过程中引入收敛速度因子,针对存在干扰的输入受限系统给出如下不变集条件。
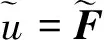
(9)
则ε(P,ρ)为收缩不变集,且从椭圆ε(P,ρ)内出发的系统轨迹将指数收敛到原点。
证明:
取Lyapunov函数V(x)=xTPx,由式(5)可得:
(10)
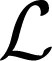
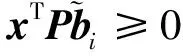
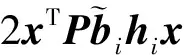
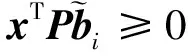
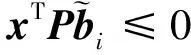
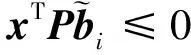
综上可得:
由上式及P为正定阵可得:
(11)
由于:
再利用式(6)可得:
(12)
将式(11)和(12)代入式(10)可得:
(13)
利用式(9)和(13)可得:

(14)
积分式(14)可得:
V(t) (15) (16) 因此,椭圆ε(P,ρ)为收缩不变集,并且从椭圆ε(P,ρ)内出发的系统轨迹将指数收敛到原点。在此不变集内系统轨迹的收敛速度与参数β密切相关。β越大,系统轨迹越快趋近于原点,控制系统的动态性能越好。 2.2 控制器设计 借鉴参考文献[11],利用形状参考集来寻找吸引域内的最大椭圆,进而利用最大椭圆来近似输入受限系统的吸引域。 通过求解具有指数收敛特性的最大椭圆来优化输入受限系统的状态反馈控制律,从而达到改善系统动态响应特性的目的。一方面,对于存在有界不确定性的输入受限系统保证其初值从一个较大范围出发时系统轨迹将收敛于原点;另一方面,保证系统轨迹具有指数收敛特性。 引入椭圆形状参考集: XS=ε(S,1)={x∈Rn:xTSx≤1} 其中,S为正定矩阵。 针对输入受限系统(8),将求解满足定理给出的不变集条件的最大椭圆问题转化为如下优化问题: s.t. 1)αXS⊂ε(P,ρ); ∀v∈; (17) α越大,意味着椭球ε(P,ρ)的“质量”越大。 为了便于求解式(17)给出的优化问题,需将式(17)给出的约束条件转化为线性矩阵不等式形式。 令γ=1/α2,Q=P-1,G=HP-1,gi表示G的第i行。将约束转化为LMI形式为: (18) 为了说明本文方法的有效性,对β=0和β=3这2种情况进行对比仿真。其中,β=0对应未考虑系统动态特性下进行的控制器设计,β=3对应考虑系统动态特性的控制器设计方法,即本文提出的控制器设计方法。 仿真中气动参数摄动范围为±50%,舵偏角幅度约束为±20°。仿真结果如图1~3所示,图1为攻角响应曲线,图2为俯仰角速度响应曲线,图3为舵偏角响应曲线。其中,虚线对应β=0,即不考虑动态特性时的响应曲线;实线对应β=3,即考虑动态特性时的响应曲线。 图1 攻角响应曲线 图2 俯仰角速度响应曲线 图3 舵偏角响应曲线 从仿真曲线可以看出,在气动参数大范围摄动且存在外界干扰的情况下,攻角回路是稳定的。引入收敛速度因子后,系统的动态特性得到明显改善,系统轨迹快速收敛,并且振荡次数明显减少。本文给出的控制方法表现出良好的稳定性和动态性能,具有很强的鲁棒性,且当控制输入触发饱和边界时系统仍是稳定的。 针对高超声速飞行器动力学模型存在不确定性以及执行机构存在控制受限等问题,基于LMI技术给出了一种具有指数收敛吸引域的控制器设计方法。将系统中的不确定性视为总和扰动,针对输入受限受扰系统提出了一种具有指数收敛速度因子的不变集条件,将控制器的设计问题转化为受限系统吸引域的最优化问题,通过求解“质量”最大的不变椭圆获得状态反馈矩阵。在气动参数摄动和控制量存在饱和的情况下,该控制方法具有良好的动态特性和鲁棒性。 [1] 胡超芳,刘运兵. 基于ESO的高超声速飞行器模糊自适应姿态控制[J].航天控制, 2015,33 (3):45-51. (HuChaofang,LiuYunbing.FuzzyAdaptiveAttitudeControlBasedonESOforHypersonicVehicles[J].AerospaceControl, 2015,33 (3):45-51.) [2] 龚宇莲,吴宏鑫. 基于特征模型的高超声速飞行器的自适应姿态控制[J].宇航学报, 2010,31(9): 2122-2128.(GongYulian,WuHongxin.CharacteristicModel-BasedAdaptiveAttitudeControlforHypersonicVehicle[J].JournalofAstronautics, 2010, 31(9) : 2122 -2128.) [3] 刘晓韵, 王静, 李宇明. 基于反馈线性化/LQR方法的高超声速飞行器姿控系统设计[J].航天控制, 2014,32(4):37-41.(LiuXiaoyun,WangJing,LiYuming.TheHypersonicVehicleAttitudeControlBasedonFeedbackLinearization/LQRMethod[J].AerospaceControl, 2014,32(4):37-41.) [4] 贺娜,姜斌,齐瑞云.基于模型预测控制的近空间飞行器容错跟踪控制[J].航天控制, 2012, 30(6): 54-58. (HeNa,JiangBin,QiRuiyun.TheFaultTolerantTrackingControlforNearSpaceVehicleBasedonModelPredictiveControl[J].AerospaceControl, 2012,30(6):54-58.) [5] 韩钊,宗群,田柏苓,吉月辉.基于Terminal滑模的高超声速飞行器姿态控制[J].控制与决策, 2013,18(2):259-263.(HanZhao,ZongQun,TianBailing,JiYuehui.HypersonicVehicleAttitudeControlUsingTerminalSlidingModeControl[J].ControlandDecision, 2013,18(2):259-263.) [6] 黄显林,葛东明.输入受限高超声速飞行器鲁棒变增益控制[J].系统工程与电子技术, 2011,33(8): 1829-1836. (HuangXianlin,GeDongming.RobustGain-schedulingControlofHypersonicVehicleSubjecttoInputConstraints[J].SystemsEngineeringandElectronics, 2011,33(8): 1829-1836.) [7] 朱凯, 齐乃明. 控制受限的BTT导弹反演自适应滑模控制研究[J].系统工程与电子技术,2011,33(5): 1094-1097.(ZhuKai,QiNaiming.AdaptiveBack-steppingSlidingModeControlforBTTMissileswithControlInputConstraints[J].SystemsEngineeringandElectronics,2011, 33(5):1094-1097.) [8] 胡庆雷, 马广富, 姜野.控制受限的挠性航天器姿态机动自适应变结构输出反馈控制[J]. 宇航学报,2007,28(4):875-879. (HuQinglei,MaGuangfu,JiangYe.AdaptiveVariableStructureOutputFeedbackManeuveringControlforFlexibleSpacecraftwithInputConstraints[J].JournalofAstronautics, 2007, 28(4): 875-879.) [9] 杨青运, 陈谋. 具有输入饱和的近空间飞行器鲁棒控制[J]. 控制理论与应用, 2015,32(1):18-28.(YangQingyun,ChenMou.RobustControlforNearSpaceVehicleswithInputSaturation[J].ControlTheoryandApplications, 2015,32(1):18-28.) [10]SunHaibin,LiShihua,SunChangyin.AdaptiveFault-tolerantControllerDesignforAirbreathingHypersonicVehiclewithInputSaturation[J].JournalofSystemsEngineeringandElectronics, 2013,24(3): 488-499. [11]MulderEF,KothareMV,MorariM.MultivariableAnti-windupControllerSynthesisUsingLinearMatrixInequalities[J].Automatica, 2001, 37(9): 1407-1416. [12]HuT,TeelA,ZaccarianL.NonlinearL2GainandGegionalAnalysisforLinearSystemswithAnti-windupCompensation[C].AmericanControlConference,Portland,USA. 2005:3391-3396. [13]RehanM,KhanAQ,AbidM,etal.Anti-windup-basedDynamicControllerSynthesisforNonlinearSystemsunderInputSaturation[J].AppliedMathematicsandComputation,2013,220:382-393. [14] 王明钊, 刘金琨. 基于LMI的挠性航天器抗饱和补偿器设计及分析[J].航天控制,2014,32(1): 63-67. (WangMingzhao,LiuJinkun.TheAnti-windupCompensatorDesignandAnalysisfortheFlexibleSpacecraftBasedontheLMIMethod[J].AerospaceControl, 2014,32(1):63-67.) [15]GuBnerT,JostM,AdamyJ.ControllerDesignforaClassofNonlinearSystemswithInputSaturationUsingConvexOptimization[J].SystemsandControlLetters, 2012, 61(1): 258-265. [16]HuTingshu,LinZongli,ChenBM.AnAnalysisandDesignMethodforLinearSystemsSubjecttoActuatorSaturationandDisturbance[J].Automatica, 2002, 38(2): 351-359. [17]KimSH.H∞Output-feedbackLPVControlforSystemswithInputSaturation[J].InternationalJournalofControl,Automation,andSystems, 2012, 10(6): 1267-1272. [18]ZhanST,YanWX,FuZ,etal.AnOptimalFeedbackApproachfortheStabilizationofLinearSystemsSubjecttoInputSaturationandMagnitude-boundedDisturbances[J].LectureNotesinComputerScience, 2013,8103(1):202-213. [19]MracekCP,RidgelyDR.MissileLongitudinalAutopilots:ConnectionsBetweenOptimalControlandClassicalTopologies[C].AIAAGuidance,Navigation,andControlConferenceandExhibit,California. 2005:6381-6409. Exponential Convergence State Feedback Control for Hypersonic Vehicle with Input Constraints Guan Yingzi1, Zhu Kai2 1. School of Astronautics, Harbin Institude of Technology, Harbin 150001, China 2. Beijing Institute of Aerospace Technology, Beijing 100074, China Regardingstabilitycontrolofahypersonicvehicleinthepresenceofinputsaturationanduncertainties,acontrollerwithexponentialconvergencerateisdesigned,whichisbasedonLMItechnique.Theuncertaintiesofhypersonicvehiclemodelareregardedas“totaldisturbance”,anexponentialconvergenceconditionforinvariantsetofsystemssubjecttoinputsaturationanddisturbanceisderived.ByusingLMItechnique,controllerdesignistransformedintomaximizationofthedomainofattraction.Thesimulationresultsshowgooddynamiccharacteristicsandrobustnessoftheproposedmethodinthepresenceofaerodynamicdispersionandcontrolinputsaturation. Hypersonicvehicle;Inputconstraints;Uncertainties;Linearmatrixinequalities(LMI);Exponentialconvergence 2016-12-12 关英姿(1968-),女,哈尔滨人,博士,教授,主要研究方向为航天器动力学与控制;朱 凯(1982-),女,哈尔滨人,博士,工程师,主要研究方向为先进控制理论在导弹制导和控制中的应用。 V448 A 1006-3242(2017)03-0034-06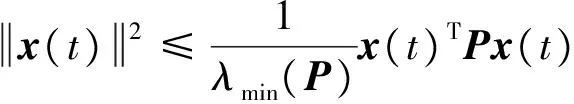
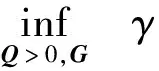
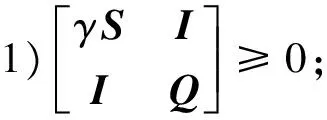
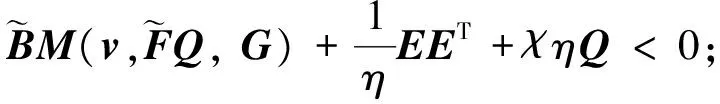
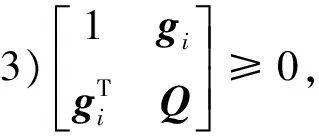
3 仿真研究
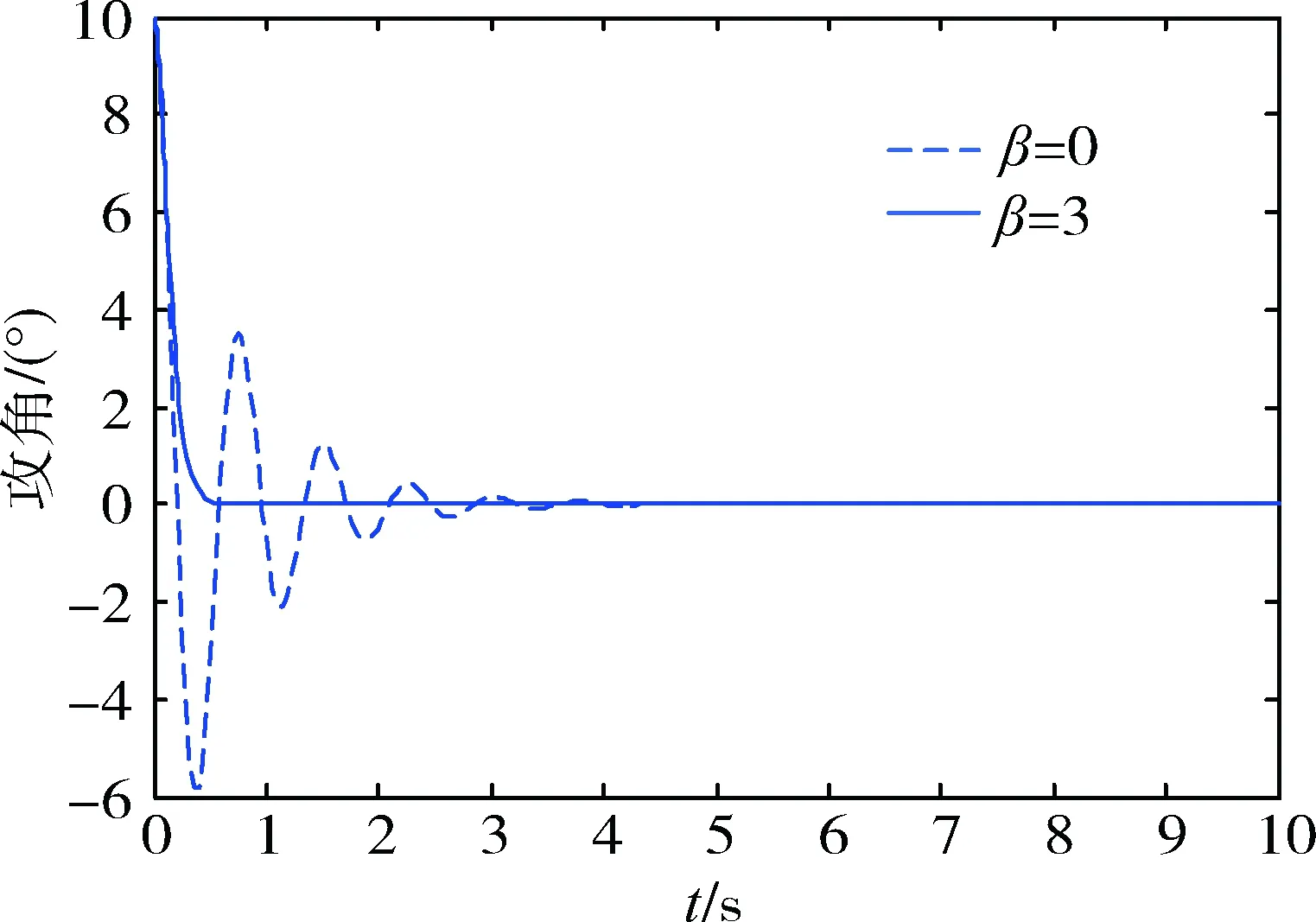
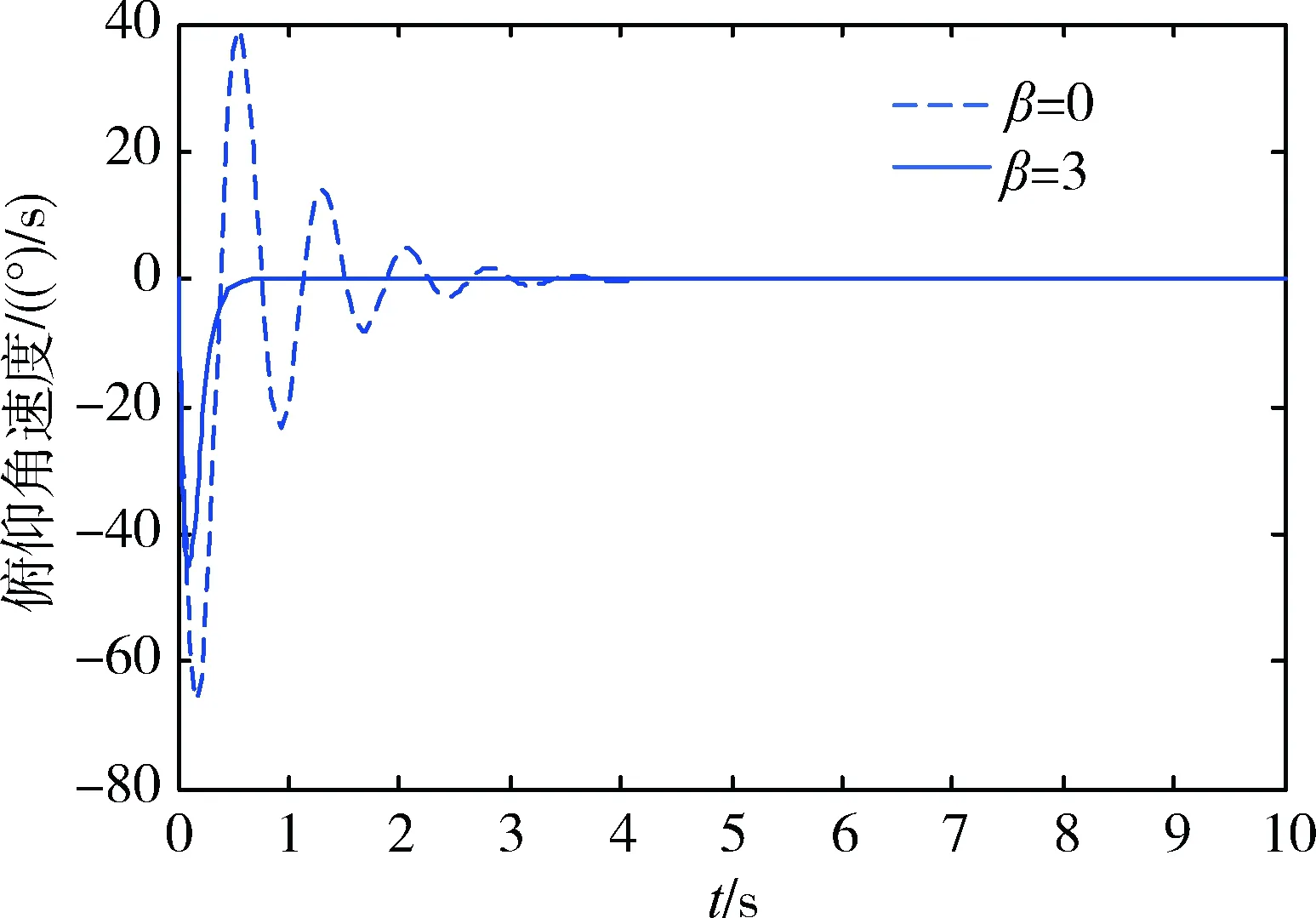
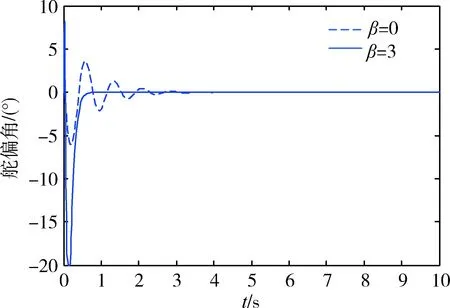
4 结论
