找准数学背景，巧解物理问题

彭立君

(湖南省岳阳市第一中学，湖南 岳阳 414000)



找准数学背景，巧解物理问题

彭立君

(湖南省岳阳市第一中学，湖南 岳阳 414000)

物理问题的解答一般是把物理过程分析与数学技巧相结合，本文介绍一例少见的利用了双曲线方程进行求解的问题.

数学背景；物理问题；双曲线

物理问题的解答一般是把物理过程分析与数学技巧相结合，解答过程中常常利用“圆”、“二次函数”、“三角函数”、“数列”知识进行处理，单纯的数学解法往往会失去物理特征，从而增加解题难度.但有一些问题隐藏着数学背景，如果能够找出数学背景，解答也会变得简洁清晰.

下面一例少见的利用了双曲线方程进行求解.

如图1所示，一艘海轮用船上天线D向海岸边的信号接收器A发送电磁波脉冲求救信号．信号接收器和船上天线的海拔高度分别为AB=H和CD=h.船上天线某时刻发出一个电磁波脉冲信号，接收器接收到一个较强和较弱的脉冲，前者是直接到达的信号，后者是经海平面反射后再到达的信号，两个脉冲信号到达的时间间隔为Δt，电磁波的传播速度为光速c，求船上天线发出信号时海轮与海岸的距离L.

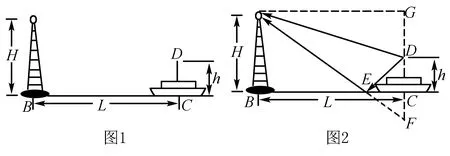
一般的求解过程如下：

如图2所示，从船上天线D向接收器A发出的电磁波脉冲信号，一方面沿直线DA直接传播到A，另一方面经过海面E点反射沿折线DEA传播到A.

由两点间距离公式可得(ct1)2=(H-h)2+L2，(ct2)2=(H+h)2+L2.根据题意有t2-t1=Δt，然后联立可解.

本题看似就此解决问题，但在实际求解计算过程中，却是很复杂的，学生一般列完方程抄了个答案了事.

有没有更好解决问题的办法呢？可以利用双曲线方程来求解.

旋转上解图形如图3所示，以C点为坐标原点，建立坐标如图，标出各点坐标，列出题意方程：

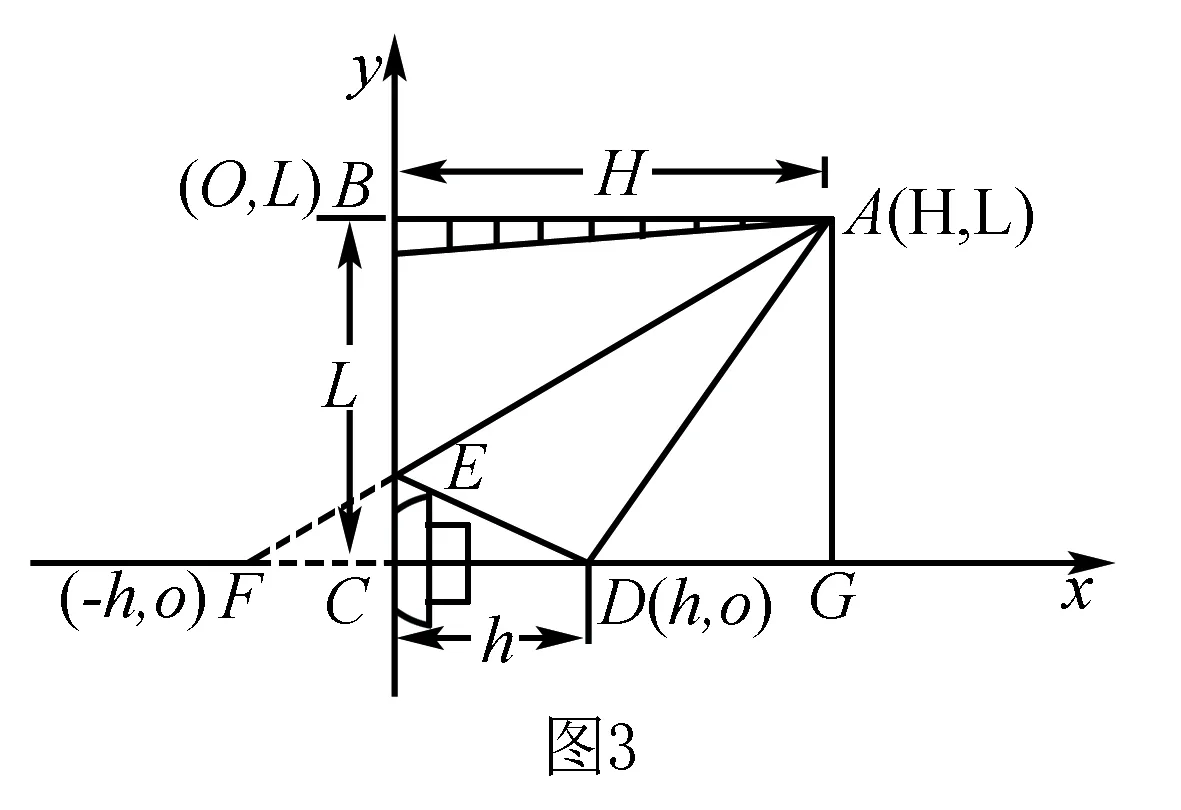
很明显，A(H,L)到F(-h,0)和D(h,0)两定点距离之差为定值cΔt.动点到两定点的距离之差为定值即为双曲线方程，即A、F、D三点满足数学的双曲线关系，其中A为双曲线上的点，D、F为双曲线的焦点.

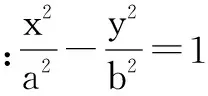
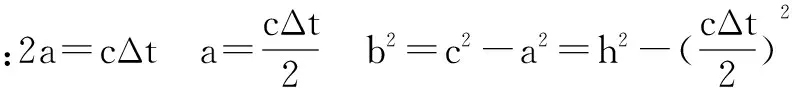
由题图3可知，当x=H时，y=L，则

物理问题一般充分利用本身所具有的物理特征求解会比较简单，本例却是有些特殊，物理过程列出方程相当简洁，但要求出结果却很困难，而利用双曲线知识会让求解过程变得直截了当，是一类相当有趣的解法.

[1]827858797.2016物理高三一轮复习物理课时作业1[DB/OL].百度文库，2016-09-13.

[责任编辑：闫久毅]

2017-05-01

彭立君(1970.11-)，男，湖南岳阳，中学高级，大学本科，从事高中物理教学与研究.

G632

B

1008-0333(2017)16-0066-02