“突破常规”别样解题也精彩
——从一道高考立体几何复习题谈起
2017-07-21常晓兵
常晓兵
(新疆大学附属中学,新疆 乌鲁木齐 830000)
“突破常规”别样解题也精彩
——从一道高考立体几何复习题谈起
常晓兵
(新疆大学附属中学,新疆 乌鲁木齐 830000)
本文试图利用课堂上实际解决一道立体几何题目的过程,向学生展示如何写出动点坐标,引导学生利用已知的知识,例如平面内的直线方程,解决空间点的坐标问题.同时,想说明解题无定法,不能有固定思维.立体几何题目的一问就用传统的方法解决,第二问就建系,需要具体问题具体对待.探寻解决问题的最好方法,用学生最易理解的方法解题.
集合题目;解题方法
立体几何是培养学生空间想象能力最有力的工具,也是高考的重要考点,空间向量为解决立体几何问题提供了一个十分有效的工具.因此人教版数学选修2-1第三章“空间向量与立体几何”对此进行了专题研究.但在实际教学中笔者发现:目前高考的立体几何问题一般分为两小问,第一小问多为空间中各种几何元素的位置关系的问题;例如:要求证明线面垂直、面面垂直、线面平行等等;而第二小问多为求二面角、空间距离的问题.由于题目的固定性,导致解题方法也比较固定,一般学生在解决第一小问通常采用传统方法,即利用学习过的判定定理、性质定理及各种推论;解决第二小问一般采用建立空间直角坐标系,利用法向量的夹角与二面角的关系求解.但笔者也发现,目前理科的立体几何题目的出题者有意识的在加大难度.调整考察角度,如下题:
题目:如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论;(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.

分析 本题第一小问涉及到动点P的位置的确定,学生对该类题目的解答不太熟悉,若采用传统方法解题,势必落入作多条辅助线的困境,对学生的空间想象能力的要求较高;而标准答案也是采用了传统方法解答.第二小问求二面角的平面角的余弦值,大多数学生都会采用建系的方法,利用空间直角坐标系解答.从表面上看这样做是比较合理的,但实际在解题过程中会发现,这样做就落入了出题者的陷阱,大量的计算使学生疲于应付.最终笔者引导学生尝试第一问就建系,看看能否解决问题.

此时有同学提出这样的证明不完备,理由是甲同学事先如何知道P为BC的中点?
笔者抓住这个契机,就问大家那么怎样解决这个问题呢?从甲同学的证明过程看,点P的确满足题目的要求啊!此时乙同学举手说到,应该设点P的坐标为(x,y,z),利用题目給出的条件解出坐标的值.笔者接着问:“点P的坐标有三个未知数,需要三个方程,那么请同学们找出三个方程解出坐标的值,这时有同学提出解不出来,条件不够;乙同学又说:点P在xOy平面内它的竖坐标为0.大家的情绪又被调动起来了,这时只需要两个方程就可以解出来了.笔者给同学们几分钟的时间讨论,突然同学丙举手说:老师,点P在直线BC上,能否利用直线的方程找到x与y的函数关系,这样就只需要一个方程.但有同学提出,在空间中的直线方程没学过啊!丙同学说:直线BC就在平面xOy内,能否在平面直角坐标系中建立x与y的函数关系,然后求解.
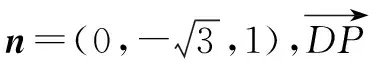

(2)过B作AC的平行线l,过C作l的垂线交l于点G,连接DG.因为ED∥AC,所以ED∥l,则l是平面EBD与平面ABC的交线.因为平面EAC⊥平面ABC,DC⊥AC,所以DC⊥平面ABC,所以DC⊥l.又CG⊥l,所以l⊥平面DCG,所以l⊥DG,所以∠DGC即为所求二面角的平面角.
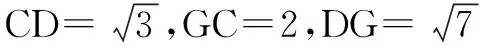

[1]人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.高中数学选修2-1(人教A版).北京:人民教育出版社,2007,第2版.
[责任编辑 杨惠民]
2017-05-01
常晓兵(1978.12-),男,本科学历,陕西米脂人,中学一级教师,从事中学数学教学.
G632
B
1008-0333(2017)16-0053-02
