提高核心素养妙解高考真题
2017-07-21刘彦永
刘彦永
(东北师范大学附属中学,吉林 长春 130021) )
提高核心素养妙解高考真题
刘彦永
(东北师范大学附属中学,吉林 长春 130021) )
本文通过对2016年课标Ⅰ卷高考压轴试题的分析和求解过程阐述,浅谈试题命制和解答中蕴含的数学核心素养以及培养学生数学核心素养的必要性和重要性.
数学;核心素养;高考真题
从双基教学的产生,到情感态度价值观、学生学科核心素养等一系列理念的提出、研究和实施,教育教学目标的实施逐步具体、明确、可操作.数学素养是相对于其它素养而言的,是专指一个人在事情处理过程中体现出的数学方面的素质与水平的高低,或者是情境中某些因素激发了个人的数学的认知结构,从而使得个人更多地从数学角度来看待问题.素养离不开具体的情境,数学素养只有在解决问题中才能体现出来,没有具体的情境,就无法判断一个人的数学素养的高低.2016年高考数学试题充分体现了数学的六大核心素养(包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析),对深化课程改革、教材更新、引领数学教学等起到了积极的导向作用.通过分析其典型试题的试题命制、解答过程,能更具象化地揭示其所蕴含或要求的核心素养,也更有利于强化培养学生数学核心素养的理念.
一、试题分析——试题命制蕴含核心素养
本文以2016年课标1卷压轴题为载体,浅谈试题所蕴含的数学核心素养以及提高数学核心素养的必要性和重要性.试题呈现(2016课标1理21)如下:
已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.
(Ⅰ)求a的取值范围;
(Ⅱ)设x1,x2是f(x)的两个零点,求证x1+x2<2.
本题已知条件简明扼要,问题却又内涵丰富,让笔者“一见钟情”.第一问是已知函数零点个数求参数范围的问题,第二问本质是函数的极值点偏移问题.既考查学生的数形结合、分类讨论、函数方程和等价转化等数学思想,又考查学生分析问题和解决问题的能力,故是一道综合考查核心素养的绝佳好题.通过试题的解答过程,可进
一步体会所蕴含的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等数学核心素养.
二、试题求解——试题解答体现核心素养
问题(Ⅰ)的解法探究
问题(Ⅰ)属于含有参数的函数问题.对于该类问题的解答,方法很多,而不同的方法也需要或体现出解题者所具备的不同的数学思维品质、关键能力等数学核心素养.
方法一:分离参数法
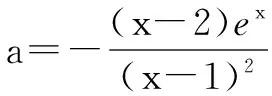
方法二:分类讨论法
对于已知函数零点个数求参数范围的问题,分类讨论也是解决这类问题的有效“利刃”.对函数f(x)=(x-2)ex+a(x-1)2求导可得f′(x)=(x-1)(ex+2a),问题便转化为探讨导数何时为正何时为负.进一步而言,如何对参数进行讨论呢?这个时候可以先讨论我们最“喜欢”的情形,即a=0时的情况,从而也可以确立分类讨论的标准.
①当a=0时,f(x)=(x-2)ex有且只有1个零点,不符合题意.
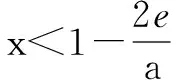
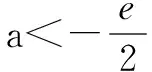
综上所述,当a>0时f(x)=(x-2)ex+a(x-1)2有两个零点.
问题(Ⅱ)的解法探究
问题(Ⅱ)属于双变量问题.该类问题的解法不一,各解法过程也蕴含着不同的数学思维品质、关键能力等数学核心素养.
方法一:利用已知条件统一变量
由(Ⅰ)知a>0,不妨设x1<1
方法二:构造对称差函数

对于本题,构造H(x)=f(1+x)-f(1-x)=(x-1)ex+1+(x+1)e1-x,x∈(0,+∞),求导数就有H′(x)=x(ex+1-e1-x)=ex(ex-e-x)>0 ,H(x)在(0,+∞)上单调递增且H(0)=0,故H(x)>0恒成立.由(Ⅰ)知x1<1
即H(x2-1)=f(1+x2-1)-f[1-(x2-1)]=f(x2)-f(2-x2)>0,故f(x2)>f(2-x2).
由f(x1)=f(x2)=0,知f(x2)=f(x1)>f(2-x2).因为x1<1,2-x2<1,且f(x)在(-∞,1)单调递减,故x1<2-x2,即x1+x2<2.
上述两个典型问题的解答都充分体现了数学核心素养对解题的思路引领.解法分别建立了对应的数学模型,通过逐步深入的逻辑推理和数据分析、数学运算简化问题,最后使问题得以轻松解决.
三、试题讨论——提高核心素养的必要性、重要性
本题由浅入深,对计算难度、思维深度的要求逐步提高,很好地体现了数学的科学性、应用性和创造性.其考查层次分明,区分度较高,使考生充分展示理性思维的广度和深度,突出选拔功能和对学生数学核心素养的考查.近几年的高考压轴题都有明显考查学生数学素养的倾向,这也昭示着提高学生数学核心素养是十分有必要的.
数学核心素养是一个高度抽象的思维产物,它要高于数学知识、数学一般的思维方法,因此有人认为数学核心素养是指把所学的数学知识都排除或忘掉后剩下的东西,即能从数学的角度看问题,有条理地进行理性思维、严密求证、逻辑推理和清晰准确地表达的意识与能力.但是它同时又不可能脱离这些下位的知识与方法,它只能在数学知识的学习过程中,数学思想方法的掌握过程中,通过逐步积累、领悟、内省形成. 发展学生的数学核心素养,有利于学生学会用数学眼光观察世界,用数学思维分析世界,用数学语言表达世界,有助于发展学生的思维品质,形成理性精神、批判思维等.然而,培养学生的数学核心素养,不是短时间内就能形成的,需要长期的坚持和引导.弗赖登塔尔认为,数学教育方法的核心是学生的再创造.教师应该创造合适的条件,让学生在学习数学的过程中,用自己的体验,用自己的思维方式,重新创造有关的数学知识.在实际教学过程中,广大一线教师要结合具体的教学内容和创设情境,让学生亲自去感受、体验、思考、动手做、总结和反思,才能有效地促进学生的数学核心素养的培养与提高.
[1]中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2003.
[2]王尚志. 如何在数学教育中提升学生的数学核心素养[J]. 中国教师, 2016(9).
[责任编辑:杨惠民]
2017-05-01
刘彦永,男,硕士,中教一级教师,数学奥林匹克竞赛教练员.
G632
B
1008-0333(2017)16-0044-03
