多角度、深探究——由一道数学质检题引发的思考

蔡贵斌

(福建省漳州外国语学校，福建 漳州 363000)



多角度、深探究
——由一道数学质检题引发的思考

蔡贵斌

(福建省漳州外国语学校，福建 漳州 363000)

本文通过对一道质检题进行多向探索，灵活转换，给出多种解法，培养学生合作交流和自主探究，以使学生的认识逐步深化，思路日见开阔，使学生做到知识学习和能力培养的协调发展，提高总复习的有效性.

一题多解；复习；解三角形；数学核心素养

在总复习中应该精选例题，善用一题多解，精准训练，进行有效复习，让学生从例题中探究解题规律，反复归纳、类比拓展，经历数学学习过程，体验解决数学问题的一般规律，并从数学思想方法的高度去分析、探究新的习题，提高高考总复习的有效性.

一、多角度评析例题

例1 (2017福建质检)△ABC中，角A,B,C的对边分别为a,b,c,2bcosC-c=2a.

(Ⅰ)求B的大小；

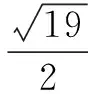
考点分析 本小题主要考查正弦定理、余弦定理、两角和与差的三角函数公式等基础知识，考查运算求解能力，考查函数与方程思想、化归与转化思想等.

思路分析 对于(Ⅰ)问可以有两种思路： 1.用余弦定理进行转化化简可得； 2.用正弦定理进行转化化简可得.

对于(Ⅱ)问由于题目给出的条件是中线长，所以可以利用同角余弦值相等，然后用余弦定理进行计算，也可以用向量通过构造平行四边形，也可以用坐标化.

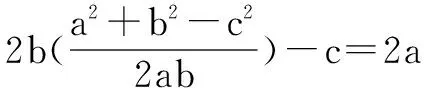
(Ⅱ)由(Ⅰ)得，b2=a2+c2+ac=c2+3c+9.①

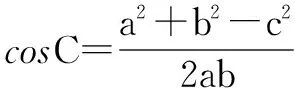
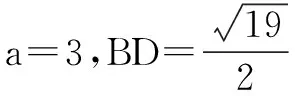
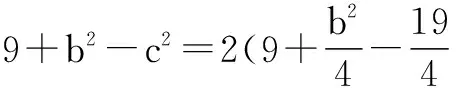
把①代入②，化简得c2-3c-10=0,

解得c=5,或c=-2(舍去)，所以c=5.

解法点评 以上解法实际上是解三角形的常规思路，利用同角的余弦值相等，只是计算量相对大一些，但属于通法.

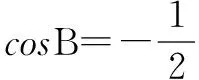
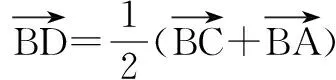
解法点评 在解法二中主要是由已知AC边上的中线长，所以联想到向量的加法.

其实解法三与解法一用的知识点实际上是一样的，只是在原来的基础上利用已知中点找中点.

由以上三种解法可见：对于《解三角形》的问题我们一般可以从正弦定理或者余弦定理入手解决我们的第一小问，至于第二小问解决的途径因题而异，但主要的思路大体可以归结为如下几种：(1)利用正弦定理或余弦定理；(2)利用余弦定理结合不等式；(3)利用正弦定理及其两角两角和与差的三角函数公式等基础知识；(4)从已知图形构造平行四边形或者三角形结合余弦定理；(5)利用中点或者几等分点结合向量；(6)利用直角坐标进行坐标化解题.

二、对教学的启示

1.建构知识形成知识网络体系

在分析例1时，我们可以引导学生构建知识体系，关注概念的生成，关注知识的逻辑系统和网络结构.比如说在解决例1的第一步时，我们可以给学生复习正弦定理和余弦定理以及两角和与差的三角函数公式等基础知识、向量的相关知识等，通过这些知识的复习，让学生把所学知识综合起来，串点成线、连线成网形成有机的整体，从而提高学生的综合运用能力.

2.重视思维能力的培养

在复习《解三角形》时，一部分学生不满足于前面总结的方法一和方法三直接用余弦定理进行求解，他们还从不同的视角总结出利用向量、构造平行四边形、图形坐标化等不同解法.这样，学生从数学探究活动中不仅学到了知识，重要的是培养了综合能力，从而提高了学生的数学素养.

3.把核心素养贯穿于数学教学整个过程

教什么，如何教？这是教师教学的永恒话题.基于数学核心素养的数学教学要更新观念提升核心素养将“学生为本”的理念与教学实际相结合.

(1)整体把握数学课程：因此在解决例1中首先要整体把握三角函数课程内容结构——利用已知条件分析问题——解三角形——正余弦定理及其两角和与差的三角函数公式等基础知识进行转化，除此以外还可以从向量的角度，几何的角度去思考，对这一过程学生不断感悟、理解抽象、推理，从而改善思维品质.

(2)从例1中我们还可以进行主题单元教学：所以在教学中我们可以进行整体分析，分析如下：首先对重点(本质、核心素养)的分析，在这节中我们最重要的是让学生把握好正余弦定理的运用以及从本题联想到向量、坐标等相关知识；其次是学情分析，在解决本问题前要观察学生对三角函数、解三角形的基本知识以及通性通法的掌握情况；最后是教学方式，从学生的学情中我们再来确定是以让学生自主探究还是教师进行逐步引导.总之，主题教学的除了可以促进学生自主学习还有助于提高教师专业水平.

(3)创设合适情境：围绕教学环节，逐步引导学生思考和调动学生的积极情绪，让学生展开联想，激发学生的求知欲，唤醒长期记忆中的有关知识、经验或表象，为掌握新知识创设一个最佳的心理和认知环境，使学生爱学、乐学.在复习《解三角形》中，抛出此例题，并告诉学生：此题有五种解法，你能找出几种？激发学生的兴趣和求知欲.

三、拓展例题简析

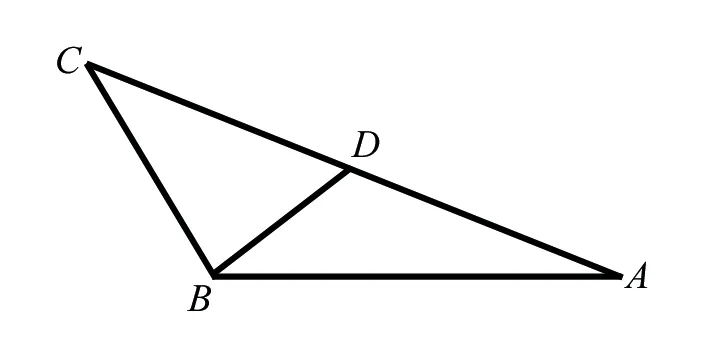
例2 (2015全国甲卷文17)△ABC中，D是BC上的点，AD平分∠BAC，BD=2DC.

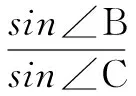
思路分析 对(Ⅰ)问：1.利用正弦定理结合已知条件直接求解； 2.作图构造直角三角形进行求解.

对(Ⅱ)问： 1.利用三角恒等变形公式得到∠B和∠C之间的一个关系式，再利用(1)的结果得出∠B和∠C之间的另一个关系式，联立求解；

2.由正弦定理得AB和AD之间的关系，进而由余弦定理得BD和AD之间的关系；

3.由正弦定理得AB和AD之间的关系，进而由余弦定理得BC和AC之间的关系；

4.取AB的中点E，连接CE，则可证明△ACE是等边三角形，△BEC是等腰三角形.由(1)和正弦定理得AB=2AC；

5. 延长AC到E，使得AE=AB，连接BE，则可证明△ABE是等边三角形.，由C是AE的中点求得.

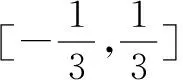
思路分析 1.利用单调递增所以导数大于等于零转化成恒成立问题； 2.利用单调递增所以导数大于等于零转化成二次函数问题； 3.应用结论“奇函数的导函数是偶函数，偶函数的导函数是奇函数”.

总之，一题多解多角度探究有助于学生对数学知识的整体建构以及理解运用，有助于学生对数学思想方法的理解运用，有助于学生分析问题解决问题的能力，有助于培养学生的创新思维能力、有助于提高学生的数学核心素养.教学经验告诉我们一题多解的精髓就是能够从不同的视角去思考问题，通过一题去整合所学知识，让学生在紧张烦闷的高三复习中找到学习的乐趣，对提高高考复习效率起到重要作用.

[1]王俭训.巧用一题多解，提高有效复习[J].东方青年教师，2010(11).

[2]朱永厂.从一道高考数学题的课堂探究说起[J].中学数学教学参考,2015(12).

[责任编辑：杨惠民]

2017-05-01

蔡贵斌,男,1986.10, 福建省龙海市,本科,中学二级职称,从事数学教学与研究.

G632

B

1008-0333(2017)16-0027-02