掌握函数与方程思想提升解题能力

牛立新

(甘肃省定西市渭源县第一中学，甘肃 定西 748200)



掌握函数与方程思想提升解题能力

牛立新

(甘肃省定西市渭源县第一中学，甘肃 定西 748200)

函数与方程思想就是利用运动与变化的观点去分析和研究数学中的等量关系.通过建立和构造函数关系，再运用函数的图象和性质去分析问题达到转化问题的目的，从而使问题得到解决，本文通过实践举例说明函数与方程思想的应用.例如恒成立问题中，数列问题中，近年高考中等，从而提升解题能力.

函数；数列；方程；解题能力

一、函数与方程思想概要

函数与方程思想：函数思想就是利用运动与变化的观点去分析和研究数学中的等量关系.通过建立和构造函数关系，再运用函数的图象和性质去分析问题，达到转化问题的目的，从而使问题获得解决，方程思想就是从问题的数量关系入手，运用数学语言将问题中的条件转化为数学模型——方程或方程组，通过解方程或方程组，或者运用方程的性质去分析、转化问题，使问题获得解决.

函数与方程思想实际上是一种模型化的思想.常见的应用有：数字问题、面积问题、几何问题方程化；应用函数思想解方程问题、不等式问题、几何问题、实际问题；利用方程作判断；构建方程模型探求实际问题；应用函数设计方案和探求面积等.

方程与函数有着必然联系，方程f(x)=0的解就是函数y=f(x)的图象与x轴交点的横坐标，函数y=f(x)也可以看作二元方程f(x)-y=0，确定变化过程的某个或某些量，往往要建立某个或某些量的方程(组)，通过解方程(组)来求得这些量.函数与方程之间可以相互转化，方程是函数关系式中的动中求静，函数则是方程的静中求动.

二、函数与方程思想实践及应用

恒成立问题中运用函数与方程思想

例1 对于满足0≤p≤4的一切实践，不等式x2+px>4x+p-3恒成立，试求x的取值范围.

解 不等式x2+px>4x+p-3恒成立，即(x-1)p+x2-4x+3>0恒成立，构造函数f(p)=(x-1)p+x2-4x+3.

当x=1时，f(p)=0,不满足f(p)>0 ∴f(p)表示p的一次函数，

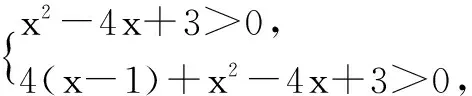
在数列问题中运用函数与方程思想

例2 设等差数列{an}的前n项和为Sn，已知a3=12,S12>0,S13<0.

(1)求公差d的取值范围；(2)指出S1,S2,S3,…,S12中哪一个最大，并说明理由.

三、运用函数与方程思想解近年高考题典例

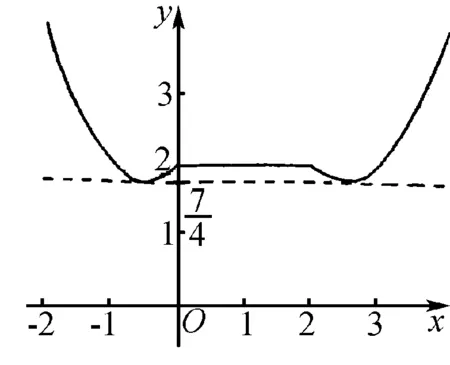
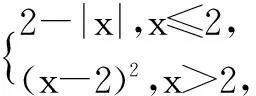
A.(7/4,+∞) B.(-∞,7/4)

C.(0,7/4) D.(7/4,2)

(1)求曲线y=f(x)在点(0，f(0))处的切线方程；

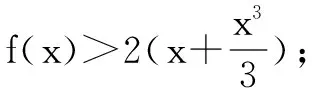
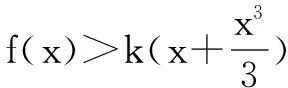
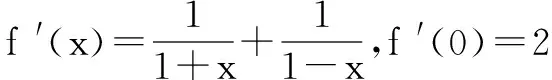
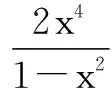
[1]薛金星.中学教材全解·数学[M].西安：陕西人民教育出版社，2009.

2017-05-01

牛立新(1968.11-)，男，甘肃省定西市，中学高级教师，本科，从事高中数学教学.

G632

B

1008-0333(2017)16-0024-02