发散思维在数列不等式解题中的运用

薛昊敏

(江苏省栟茶高级中学,江苏 如东 226406)



发散思维在数列不等式解题中的运用

薛昊敏

(江苏省栟茶高级中学,江苏 如东 226406)

能力要求成为当下高考数学命题之核心，其中数列不等式则为最常见的热点题型.通过应用递推比较大小、观察通项实现应用化归、放缩构造多维推广等教学策略实现试题的讲解能够有效引导学生深入理解数学思想方略，逐步帮助学生实现这一类型题目的完美解题，进而达到稳步提升学生知能的终极目标.

发散思维;数列不等式;解题运用

高考数学试卷越来越注重对学生能力的考查，近些年来数列不等式逐渐成为一个热点题目.数列不等式的难点在于要求学生有必要的推理能力和联想想象能力，不管是考查类比、归纳、猜测还是观察，其多元化的背景常常会让学生手足无措.考查的方式新颖化就会让学生困扰.本文将对数列不等式进行详细的讲解，从“应用递推”、“观察通项”和“放缩构造”三个方面来帮助学生理清脉络.希望通过对高考数列不等式的命题讲解，帮助学生了解数学思想方法，进而稳步提升.

一、应用递推，比较大小

对于用数列通项公式的题目，应用递推关系是最经常使用的策略，通过作差来达到实现比较大小的目的.运用递推关系，也是最考验学生基础知识是否扎实.在推导时一般是按照固定思维，只需保证缜密的思维即可.

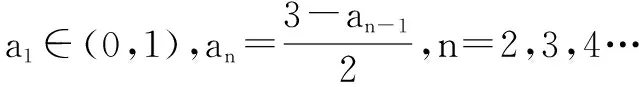
(1)求{an}的通项公式；

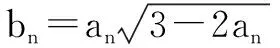
(2)有两种方法.

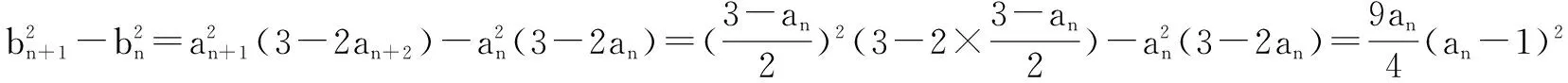
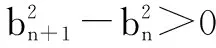
这种类型的题目主要考查学生根据条件来推导出数列关系的能力，学生只需按照规定的步骤一步一步地解答就可以了.

二、观察通项，应用化归

题目中的条件常常需要学生去观察通项，然后进行适当的变形来找到解决问题的入口.这方面的题目会将函数、导数、方程、数列和不等式结合到一起进行考查，要求学生的逻辑思维能力有待加强.

以广东高考题为例.

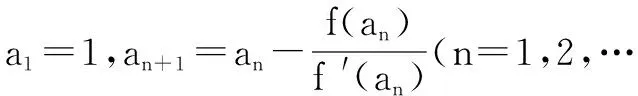
(1)求α,β的值；

(2)证明：对任意的正整数n，都有an>a1;

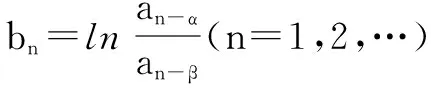
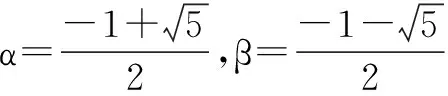
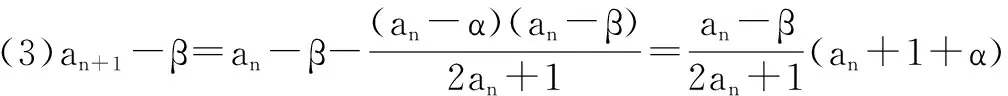
这种题目的形式多样，当时离不开数列问题的本质思想.这道题将数列和函数进行融合，将考查学生的多重思维，体现了化归的思想，有助于提升学生的综合能力.

三、放缩构造，多维推广

对数列进行放缩，是一种非常重要的思想.有关放缩的题目，需要学生进行综合分析，推理考究来进行合理的放缩才能解决题目，一般需要先求和然后进行放缩.

这类题目的难点就在于学生放缩的不恰当，进而无法去证明不等式.那么就需要教师进行必要的总结，来归纳出基本的放缩思想，这样能让学生有清晰的认知.

数列不等式的证明本来就是一个棘手的问题，必要的题目实践练习是非常有必要的，学生通过题目才能正确的明白数学方法的正确使用，正确解读何种题目用何种方法.本文只是列举了数列不等式的部分内容，笔者认为学生在题目中提取数学思想才是最重要的.

[1]李传军.证明数列不等式容易被“遗忘”的几种策略[J].才智,2009(12).

[2]翟佳妮.高中数学竞赛和高考中数列不等式的问题研究[D].西北大学,2015(6).

[责任编辑：杨惠民]

2017-05-01

薛昊敏(1987.11- )，女，江苏省南通如东人，中学二级教师，大学本科，从事高中数学教学.

G632

B

1008-0333(2017)16-0004-02