待定系数法与累加法的殊途同归
2017-07-21苏艺伟
数理化解题研究 2017年16期
苏艺伟
(福建省龙海一中新校区,福建 漳州 363100)
待定系数法与累加法的殊途同归
苏艺伟
(福建省龙海一中新校区,福建 漳州 363100)
本文举例说明了数列中可以同时采用待定系数法与累加法求通项公式的四种题型,并且迁移应用到2016年浙江省高考理科第20题.通过对这两种方法的阐述培养学生的解题能力,发散思维,提高数学核心素养.
待定系数法;累加法;核心素养
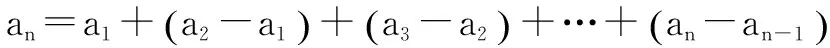
题型一 已知an+1=pan+c,其中c为常数.
法1 待定系数法
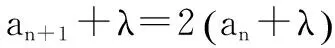
与an+1=2an+3比较系数可得λ=3.
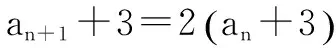

an+3=4·2n-1=2n+1,即an=2n+1-3.
法2 累加法
由an+1=2an+3
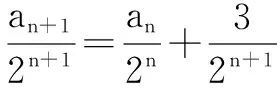
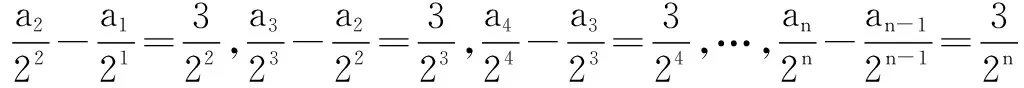
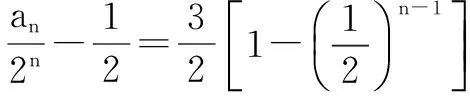
法1 待定系数法
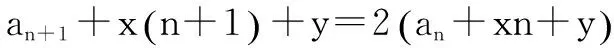
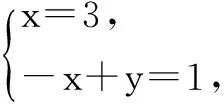
法2:累加法
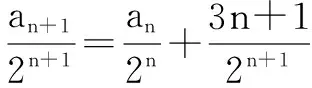
法1 待定系数法
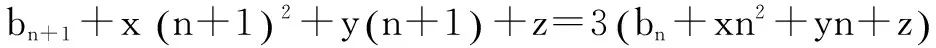
bn-n2+n+2=3n,即bn=3n+n2-n-2.
法2 累加法
由bn+1=3bn-2n2+4n+4

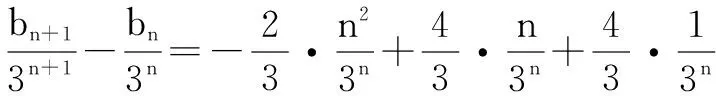
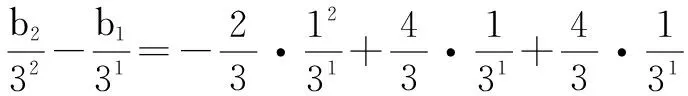
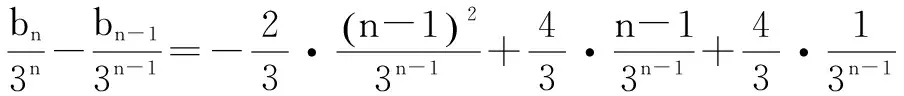
根据累加法有
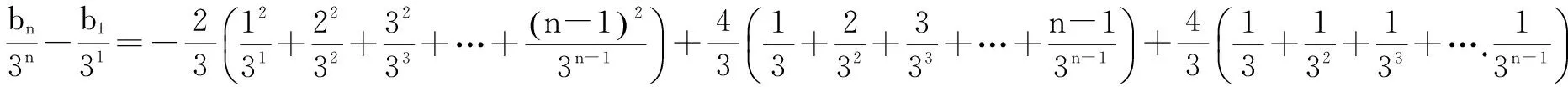

解得bn=3n+n2-n-2.
法1 待定系数法
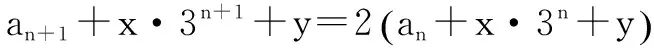
整理得an+1=2an-x·3n+y.
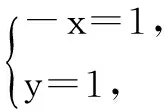
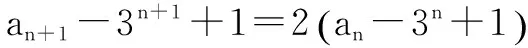
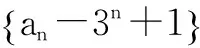
所以an-3n+1=-2n-1,即an=3n-2n-1-1.
法2 累加法
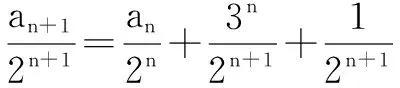
根据累加法有
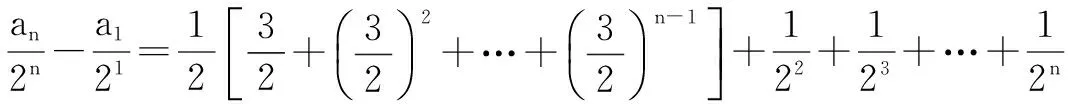
故an=3n-2n-1-1.
上述四种求数列通项公式的题型采用两种方法均可求解.在实际解题中,我们要根据题目条件灵活选取适当的方法,以达到解题的最优化,从而锻炼我们的思维能力和计算能力.
[1]鲍健,一类数列求和试题的转化和拓展[J].高中数学教与学,2017(05):20-22.
[责任编辑:杨惠民]
2017-05-01
苏艺伟(1986.05-),男,福建龙海,中学二级教师,本科学历,从事高考试题,数学教育.
G632
B
1008-0333(2017)16-0046-02
