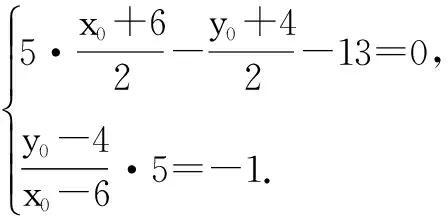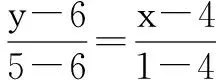直线与圆位置关系类问题的解法
2017-07-21王统文
王统文
(重庆市垫江中学校,重庆 垫江408300)
直线与圆位置关系类问题的解法
王统文
(重庆市垫江中学校,重庆 垫江408300)
直线与圆方程问题求解问题,对刚进入解析几何学习的初学者是较为困难的.怎样才能顺利完成解答是题他们非常关心的问题.本文就如何挖掘条件、怎样利用几何知识探求解决问题的途径介绍几种方法,帮助初学者树立正确理念、掌握解题方法.
直线与圆;直线与圆的位置关系;解法
直线与圆方程的求解问题,对刚进入解析几何学习的初学者是较为困难的.怎样才能顺利完成解答是他们非常关心的问题.本文就如何挖掘条件、怎样利用几何知识探求解决问题的途径介绍几种方法,帮助初学者树立正确理念、掌握解题方法.
直线与圆的位置关系的判定通常有两类方法:一是代数法,就是将直线方程代入圆方程后得到一个一元二次方程,该方程有两个不同实根(即根的判别式Δ>0)时直线与圆相交,该方程有两个相同实根(即根的判别式Δ=0)时直线与圆相切,该方程无实根(即根的判别式Δ<0)时直线与圆相离;二是几何法,就是计算出圆心到直线的距离d后,与圆半径r比较大小,当d
一、利用直译法判别直线与圆的位置关系
在求动点轨迹方程时常常用直译法.直译法就是将题设条件“翻译”为数学术语,再利用相应数学知识解决相应数学问题.这个方法同样适合判断直线与圆的位置关系,就是直接计算出圆心到直线的距离d,再与圆半径r比较大小.
例1 如果点M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,那么直线x0x+y0y=a2与该圆的位置关系是( ).
A.相切 B.相交 C.相离 D.相切或相交
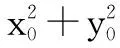
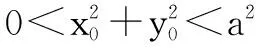
所以直线x0x+y0y=a2与圆x2+y2=a2(a>0)相离.
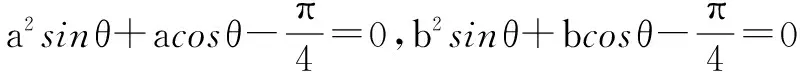
A.相切 B.相交 C.相离 D.相切或相交



所以直线与圆相交.
二、利用曲线系解决切点弦问题
从圆外一点向圆引切线,这样的切线有两条,求两条切线的方程是比较简单的.若要通过求切线方程,进而求出两切点坐标后得到过两切点的直线(通常称为切点弦)方程就比较麻烦.但是,如果利用切线垂直过切点的半径,从而判定圆心、两切点及圆外已知点四点共圆,再利用圆系,就可求出公共弦方程完成求解.
例3 过点P(3,-2)引圆C:(x+1)2+(y-2)2=9的两切线,切点为A、B,则直线AB的直线方程为____.
分析 若按常规思路求解,一般要设出切线PA、PB的直线方程y+2=k(x-3)后,利用圆心到直线的距离等于圆半径求出切线斜率k的值,再求出切点A、B的坐标,从而得到直线AB的方程.这个方法运算量较大,不宜使用.考虑到切线与过切点的半径的垂直关系,不妨利用C、A、P、B都在以CP为直径的圆上,从而AB是两圆的公共弦,问题解决就变得简单了.
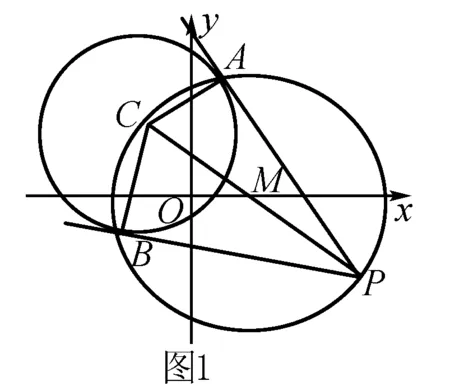
解 如图1,因为PA⊥CA,PB⊥CB,
所以C、A、P、B都在以CP为直径的圆上.
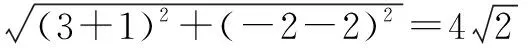
且线段CP的中点坐标为M(1,0),
所以圆M的方程为(x-1)2+y2=8.
所以公共弦AB的直线方程为
[(x+1)2+(y-2)2]-[(x-1)2+y2]=9-8,即4x-4y+3=0.
三、利用平面几何知识等价转换
解析几何法就是用代数方法研究几何问题的数学方法.在解决解析几何问题时自然要利用几何知识解决相应问题.
例4 到点A(2,3)的距离等于1的直线同时到点B(-1,-1)的距离为d,当这样的直线有4条时,则d的取值范围是____.
分析 到点A距离等于1的直线就是与以A为圆心、1为半径的圆的切线,到点B的距离等于d的直线是与以B为圆心、d为半径的圆的切线.本题的4条直线就是上述两圆的公切线,所以两圆相离.
解 由题设知|AB|>d+1,即5>d+1,所以0 例5 圆C:(x-1)2+(y-2)2=2上至少有3点到直线l:x+y+m=0的距离1,则m的取值范围是____. 分析 到直线距离相等的两个点有两种情况,一是过这两点的直线与已知直线平行,二是已知直线过这两点连线段的中点.当圆上至少有三点到直线l距离等于1时,三点中必有两点在直线l的靠近圆心的同侧,过这两点的直线l1与已知直线l平行且距离为1,另外的点在直线l的另一侧且与l平行距离也等于1的直线l2上(如图2).从而圆心C到l1的距离小于半径,到l2的距离不大于半径.由此可求出参数范围. 解 圆C:(x-1)2+(y-2)2=2的圆心C(1,2)到直线l:x+y+m=0的距离d为 当圆上至少有三个点到直线l:x+y+m=0的距离等于1时, 涉及三角形问题时,要联系三角形的解法,利用边角关系、正弦定理、余弦定理等寻找解题方法.同时,要分析问题涉及的元素特征,选择适当的三角形完成解答. 例6 直线与圆C:(x-1)2+(y-2)2=2相交于A、B两点,则正三角形ABP的顶点P到圆心C的最大距离是____. 有些试题题设条件给出的有用信息较为隐蔽,如果不能挖掘这些隐藏的对解题有用的信息就很难完成试题解答.对称性就是容易隐藏的信息,如角的两边关于角平分线对称、入射线与反射线所在直线关于反射直线对称等,解题时需重视. 例7 已知△ABC的顶点A的坐标为(6,4),∠ABC的角平分线与∠ACB的外角平分线所在直线的方程分别为x-y=0,5x-y-10=0,求边BC所在直线的方程. 分析 关于直线BC现有的已知条件很隐蔽,斜率、截距、直线上的点坐标都不是已知,要求BC的方程好像无从下手.但是,如果对角平分线有较深刻的认识,知道角的两边关于角平分线对称,求出点A关于角平分线x-y=0,5x-y-13=0的对称点A1、A2(如图4)的坐标,即可求出直线BC的方程. 利用关于直线对称解答试题时,抓住两对称点的连线与对称轴垂直,连线段的中点在对称轴上是关键. 利用对称性,还可以解决一些最值问题. [1]王统文.新课标下高中数学概念教学探讨[J].教育,2016(11):06. [责任编辑:杨惠民] 2017-05-01 王统文(1962.8-),男,汉族,重庆市垫江县人,中学高级教师,从事解题方法研究. G632 B 1008-0333(2017)16-0041-03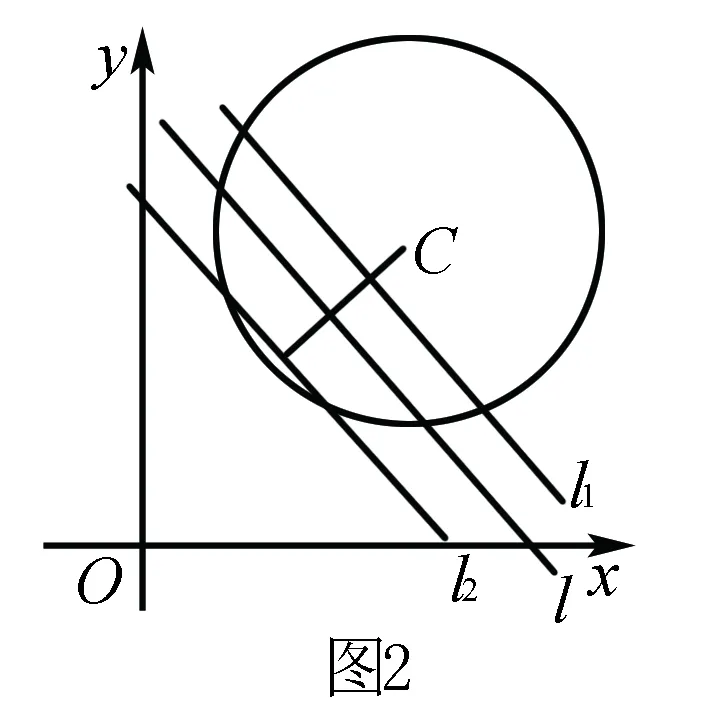
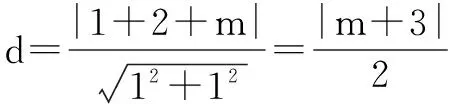


四、利用解三角形法解决有关圆的问题


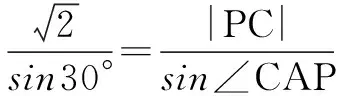
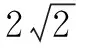
五、利用对称性求解直线与圆方程问题