例谈不等式解题中的多元性和延拓性
2017-07-21朱小扣朱嘉懿
朱小扣,朱嘉懿
(安徽省无为县牛埠中学,安徽 巢湖 238351)
例谈不等式解题中的多元性和延拓性
朱小扣,朱嘉懿
(安徽省无为县牛埠中学,安徽 巢湖 238351)
高中不等式的解题方法千变万化,其规律不易掌握.笔者通过研究发现,多元性和延拓性不等式解题中所蕴含的重要性质.本文将通过例题来阐述多元性和延拓性的应用,让学生在遇到不等式题时会举一反三,融会贯通,提升不等式的解题能力.
高中数学;不等式;多元性;延拓性
一、解题方法的多元性
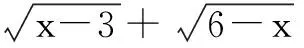
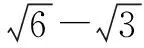
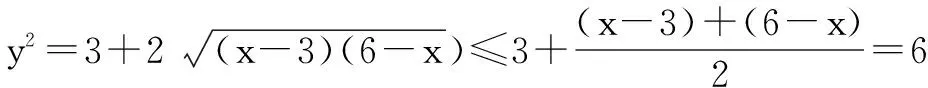
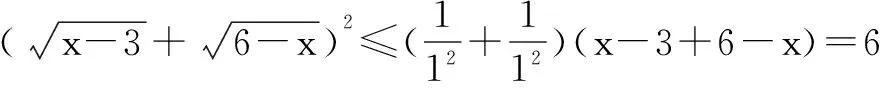
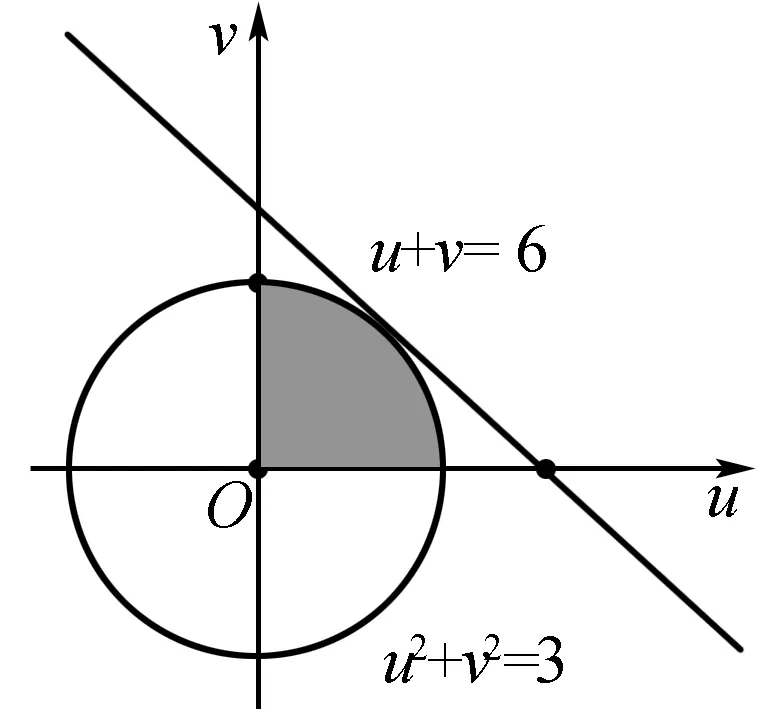
方法(4) (非线性规划法)
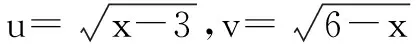
过程如下:
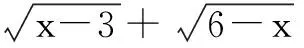
评析 一个题目要想完全搞清楚,学生做完后,就必须想一想还有没有其他的解法了?这些解法有联系吗?通过多元法的指引,使学生会一题多解,多题一解,会举一反三,这就体现了多元性的重要意义.
二、解题思路延拓性
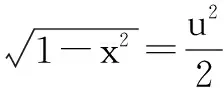
代入原函数得:
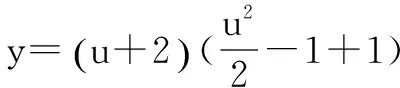
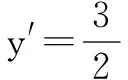
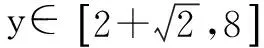
此题中换元法和平方的结合,可以使得做起来更方便.比起直接求导更简单.实际上,此方法是由平方法延拓得到的,其延拓过程如下:
又如:课本上的两个例题证明ex≥x+1,x-1≥lnx(x>0),从这两题出发,可以延拓得到了另外五个高考中多次运用的重要公式,过程如下:
ex≤11-x(0≤x≤1)
评析 一个好的题目必然要具有延拓性,使其和前面的知识达到一脉相承.通过延拓,可以让学生在做题中的思想的到发散,让学生得到新的知识,在延拓中得到自身的提高!
[1]何易阳.自主招生数学解证宝典[M].哈尔滨:哈尔滨工业大学出版社,2015:165-166.
[2]朱小扣,双绝对值不等式的求解例说[J].数理天地,2016(4):13-13.
[3]朱小扣,含有双绝值的不等式的解法五种[J].中学数学研究(华南师范大学版),2016(13):36-37.
[责任编辑:杨惠民]
2017-05-01
朱小扣(1986- ),男,安徽无为人,中学一级教师,本科,从事高中数学试题研究及竞赛.
G632
B
1008-0333(2017)16-0035-02
