求最值的常用方法
——以一道高考题为例
2017-07-21罗燕
罗 燕
(陕西省延安市吴起高级中学,陕西 延安 717600)
求最值的常用方法
——以一道高考题为例
罗 燕
(陕西省延安市吴起高级中学,陕西 延安 717600)
最值问题是一种能力考查题,它能有效地考查学生对知识和方法的综合与灵活应用.因此,求解最值问题,是高考数学中的热点,也是学生平时学习的难点.本文通过对一道高考题的研究,归纳了几种高考中常用的求最值的方法.
最值;方法;高考题
最值问题是高中数学的重要内容之一,也是高考的热点问题.它可以以求最值为载体,考查高中数学的主要知识与方法,解决最值问题要求学生要有扎实的数学基本功与良好的数学思维能力.本文试以2016年江苏高考数学试卷中的14题为例,探析最值问题在高考中的常见解决方法.
题目:在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是____.
解法一 构造二次函数求最值
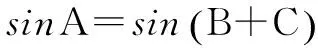
∴sinBcosC+cosBsinC=2sinBsinC,
∴tanB+tanC=2tanBtanC.
又∵tanA+tanB+tanC=tanAtanBtanC,
∴tanA+2tanBtanC=tanAtanBtanC,
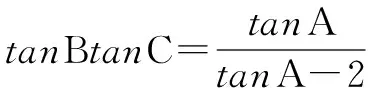
又tanBtanC>0,
∴tanA>2.
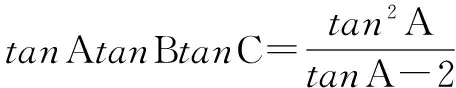

所以tanAtanBtanC的最小值是8.
点评 设法构造二次函数,利用二次函数的解析式及性质获得最大(小)值.
解法二 利用均值不等式求最小值
前面化解步骤同解法一,
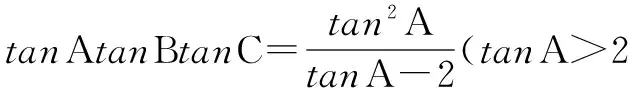
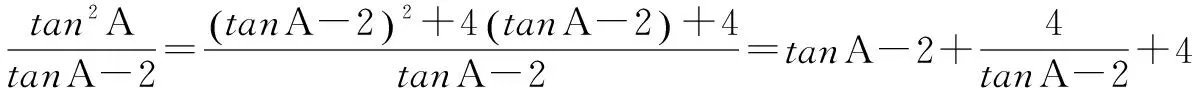
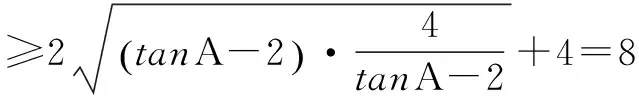
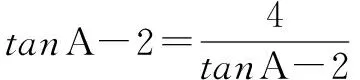
所以tanAtanBtanC的最小值是8.
点评 利用均值不等式求最值时,要注意“一正,二定,三相等”;构造“定值”,口诀是“和定积最大,积定和最小”.
解法三 利用函数单调性求最小值
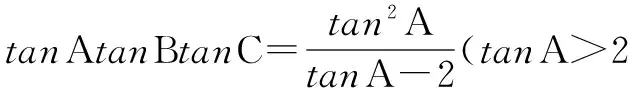

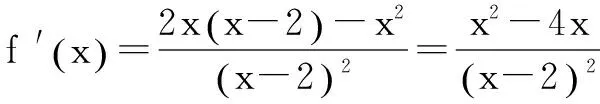
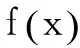
点评 利用函数的单调性求最值,需要先判断函数在给定区间上的单调性,然后结合单调性求最值
解法四 利用方程思想求最小值
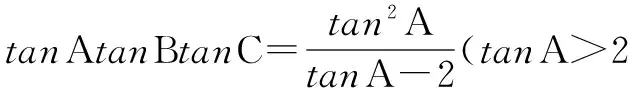
设t=tanAtanBtanC,x=tanA,
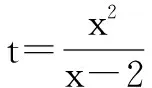

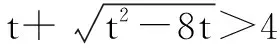
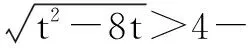
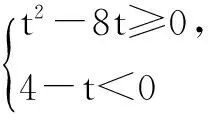
解得t≥8.
所以tanAtanBtanC的最小值是8.
方法 利用方程根的取值情况,列不等式组,然后求函数的最值.
当然,解最值问题的方法远不止这些,比如,还有三角代换法、放缩法、反函数法等等,这里仅是根据这道高考题列举了求最值问题的几种方法.另外,通过不同方法的求解,也体现出高考题的综合性.在平时的学习中,只要我们能够熟练地掌握各种方法,就能在高考场上游刃有余.
[1]代欢.高中数学函数最值问题的几种求解方法[J].理科考试研究,2017(01).
[2]王超.三角函数最值问题探究[J].理科考试研究,2014(07).
[责任编辑:杨惠民]
2017-05-01
罗燕(1985.7-),女,四川,中学二级教师,研究生,从事数学教育.
G632
B
1008-0333(2017)16-0019-02
