变参数Rayleigh型p-Laplacian微分方程周期解的存在性

陈仕洲

（韩山师范学院数学与统计学院，广东潮州521041）

变参数Rayleigh型p-Laplacian微分方程周期解的存在性

陈仕洲

（韩山师范学院数学与统计学院，广东潮州521041）

应用重合度理论和一些分析技巧，研究了一类含有变参数Rayleigh型p-Laplacian广义中立型微分方程，获得其周期解存在性的新的充分条件，推广和改进了已有文献中的相关结论.

周期解；Rayleigh型p-Laplacian方程；中立型算子；重合度

1 引言及引理

由于含偏差变元的p-Laplacian微分方程周期解存在性在生态学、物理学和控制理论等领域应用广泛，因而引起人们极大的兴趣，目前已有许多研究成果[1-7]．例如文献[5]、文献[6]研究了一类具偏差变元的Lienard型方程

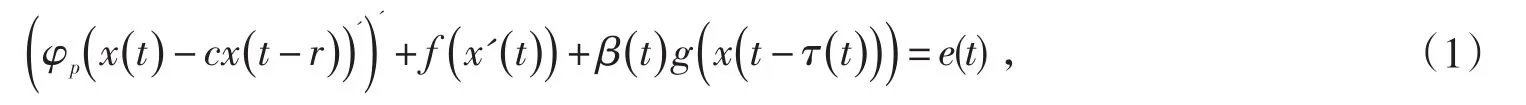
文献[7]研究了

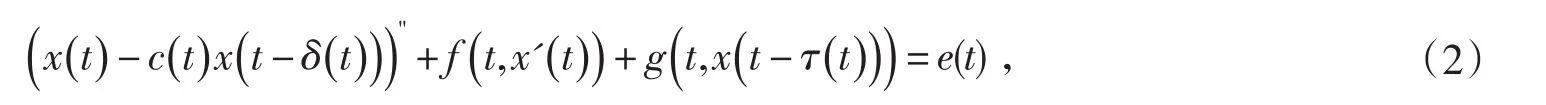
周期解的存在性．本文将应用Mawhin连续性定理和一些分析技巧，研究一类更广泛的p-Laplacian Rayleigh方程

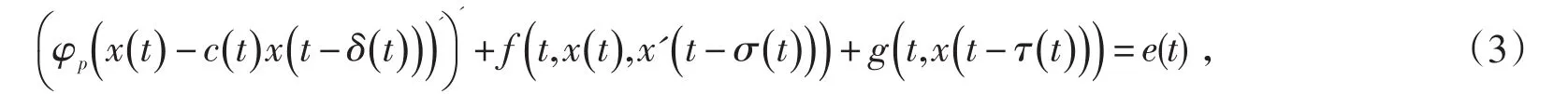
引理1[7]如果,则映射A在Ω⊆CT上存在连续逆映射A-1，满足

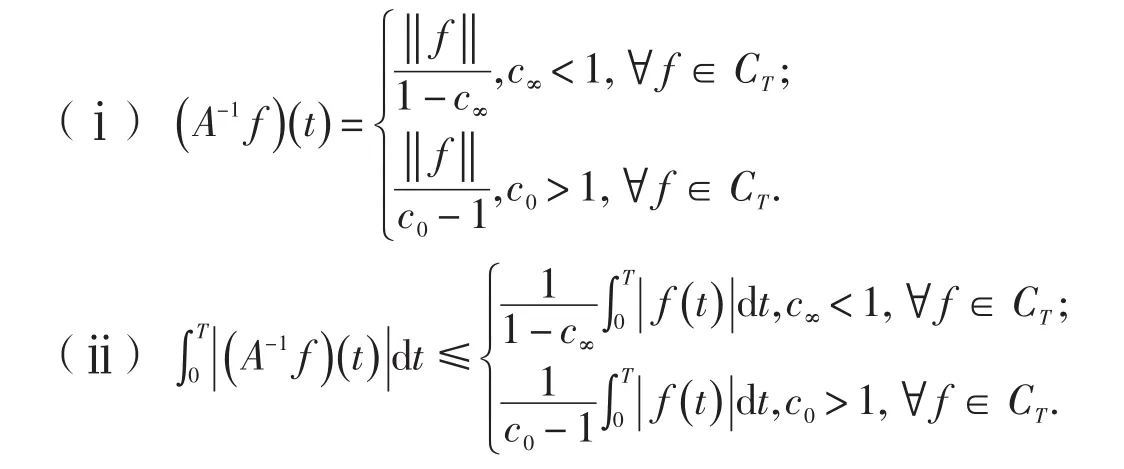
设X和Y都是实Banch空间，L:DomL⊂X→Y是指标为零的Fredholm映射，DomL表示L的定义域，即dimKerL=codimImL＜∞.，且ImL是Y中的闭集．存在连续投影P:X→X,Q:Y→Y使得

ImP=kerL,ImL=KerQ=Im(I-Q),X=KerL⊕KerP,Y=ImL⊕ImQ,

引理2[1]（Manasevich-Mawhin）设X，Y都是Banach空间，L:DomL⊂X→Y是指标为零的Fred⁃holm映射，Ω⊂X为有界开集，上是L-紧的．若下列条件成立

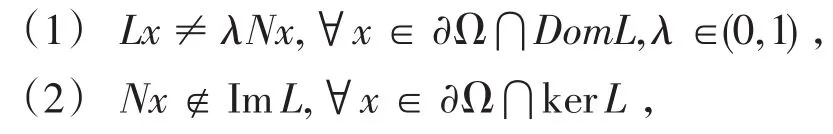
（3）deg{JQN,Ω⋂kerL,0}≠0,其中J:ImQ→KerL是一个同构.

引理3[8]设

为应用引理2，改写方程（3）为如下形式：

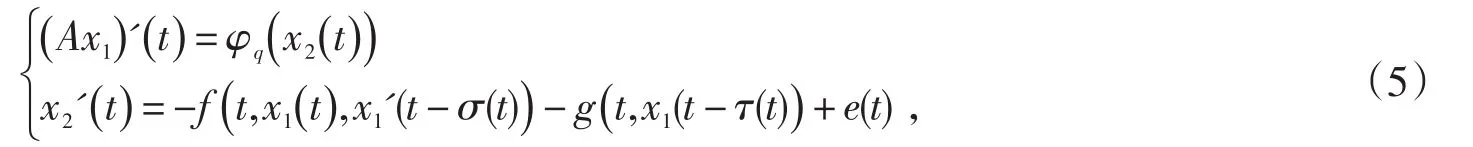
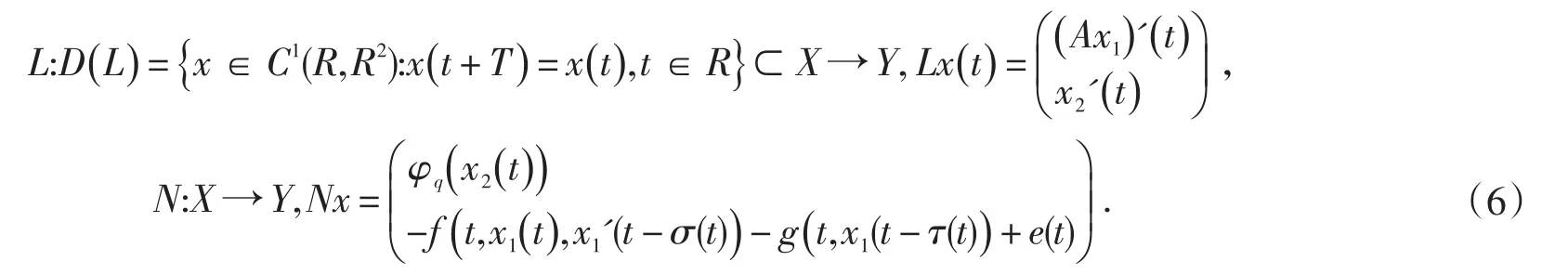
显然方程组（5）等价于Lx=Nx.

由L的定义，可以得到

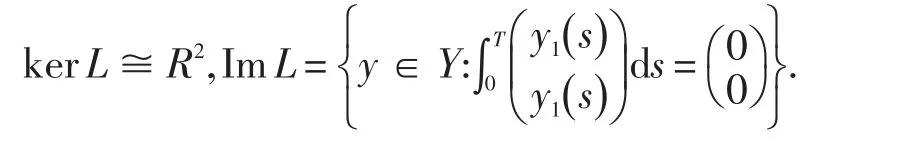
因此L是指标为零的Fredholm映射．定义映射P:X→X,Q:Y→Y

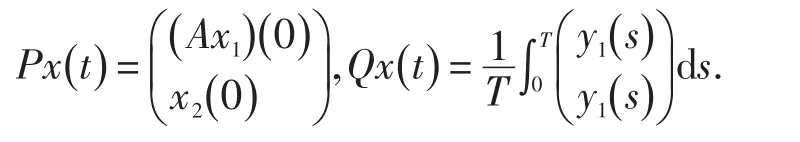
2 主要结论

定理1设存在常数r1,r2,r4,k1,k2,k3≥0;d＞0,r3＞r1满足：

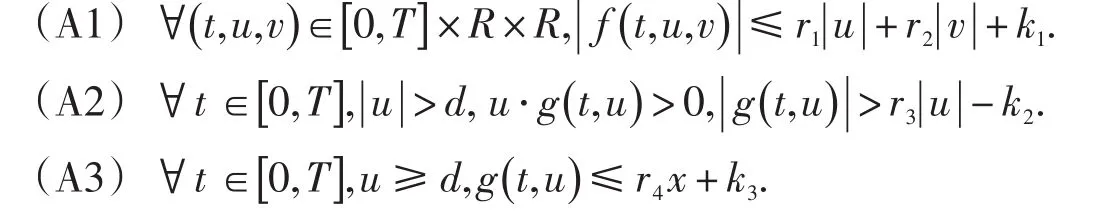
（A4）下列条件之一成立：

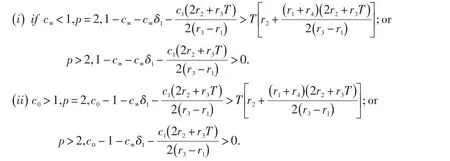
则方程（3）存在一个T-周期解.

证明考虑方程Lx=λNx,λ∈(0,1).即

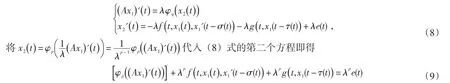
对（9）式两边在[0,T]上取积分可得

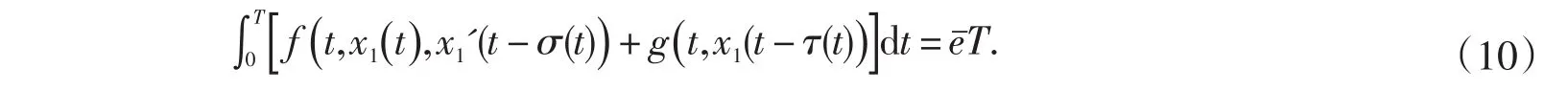
根据积分中值定理，∃t1∈[0,T],s.t.

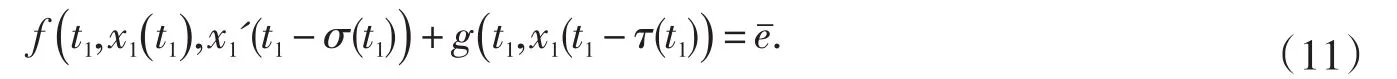
我们断言：∃t2∈[0,T],s.t.

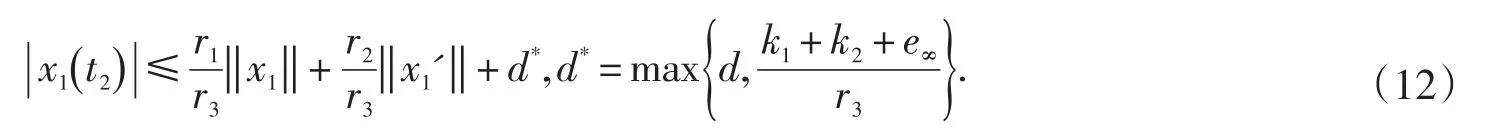
下面分两种情形证明断言（12）成立：

情形1如果|x1(t1-τ(t1)|≤d，则显然有

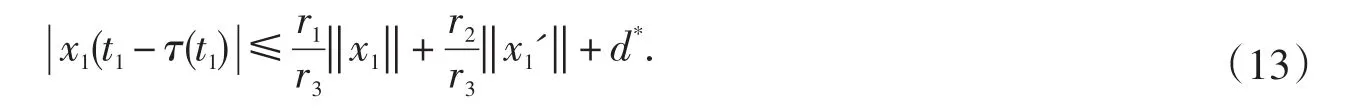
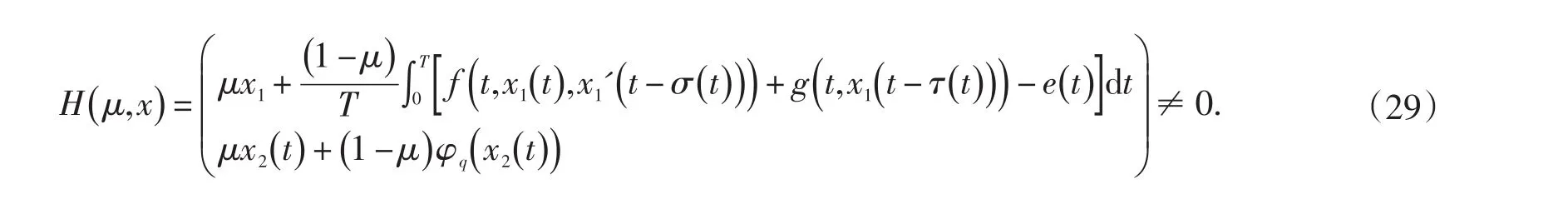
因而

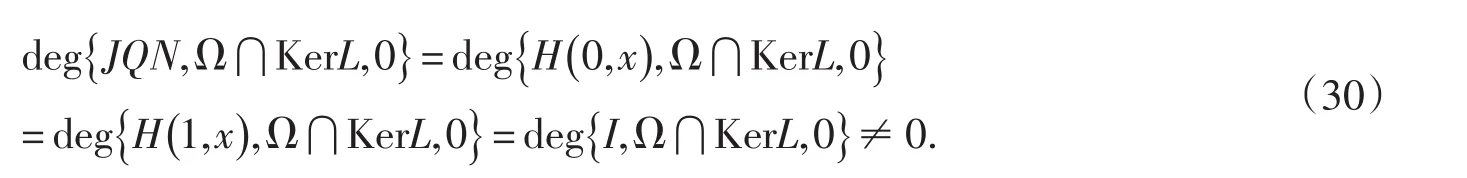
故引理2的条件（3）被满足．根据引理2知，方程Lx=Nx在中有解，即x1(t)是方程（3）的T-周期解.

情况（ii）如果c0＞1，由引理1，

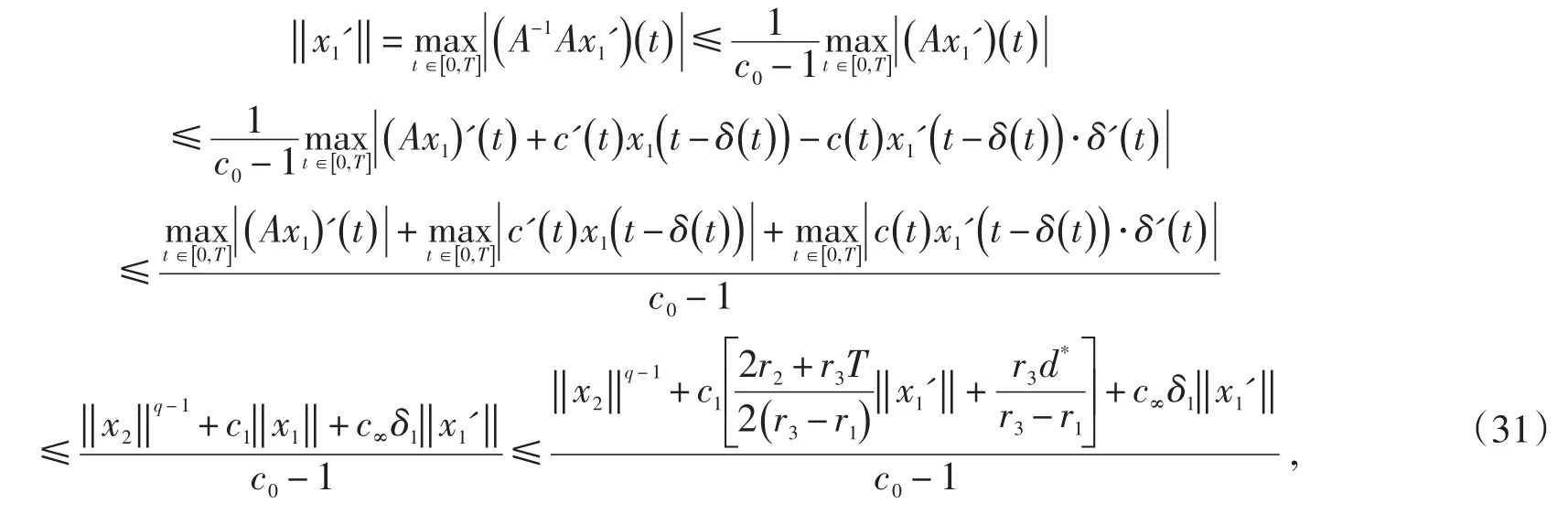
由此可得

余下部分类似于情况（i）的证明，不再赘述.

类似于定理1，容易证明

定理2定理1中的条件（A3）换为

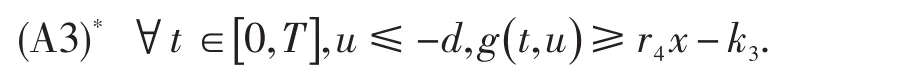
其余条件不变，则方程（3）存在一个T-周期解.

3 例子和注记

考虑中立性微分方程

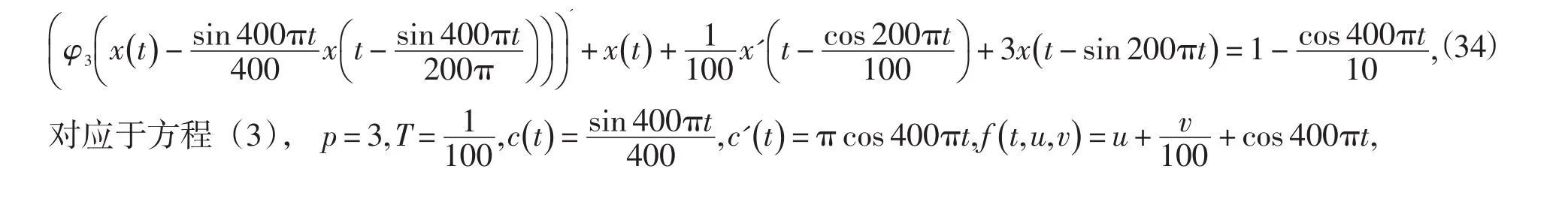
[1]MANASEVICH R,MAWHIN J.Periodic solutions for nonlinear systems withp-Laplacian-like operators[J].J.Differential Equations,1998,145(2):367-393.

[2]XIAO B,LIU B.Periodic solutions for Rayleigh type p-Laplacian equation with a deviating argument[J].Nonlinear Analysis:Real World Applications,2009,10(1):16-22.

[3]CHEUNG W S,REN J.Periodic solutions for p-Laplacian Rayleigh equations[J].Nonlinear Analysis:Theory,Methods&Ap⁃plications,2006,65(10):2003-2012.

[4]LIU B.Existence and uniqueness of periodic solutions for a kind of Liénard type p-Laplacian equation[J].Nonlinear Analysis:Theory,Methods&Applications,2008,69(2):724-729.

[5]DU B,HU X.Periodic solutions to a p-Laplacian neutral Rayleigh equation with deviating argument[J].Applications of Mathe⁃matics,2011,56(3):253-264.

[6]HE Z M,SHEN J H.Existence of periodic solutions for p-Laplacian neutral Rayleigh equation[J].Advances in Difference Equations,2014,(1):67.

[7]XIN Y,ZHAO S.Existence of periodic solution for generalized neutral Rayleigh equation with variable parameter[J].Advanc⁃es in Difference Equations,2015,(1):209.

[8]LI J W,WANG G Q.Sharp inequalities for periodic functions[J].Applied Math.E-Note,2005,5:75-83.

Existence of Periodic Solutions for a Rayleigh Type p-Laplacian with Variable Parameter

CHEN Shi-zhou
（College of Mathematics and Statistics，Hanshan Normal University，Chaozhou，Guangdong,521041）

By application of coincidence degree theory and some analysis skills,we study a Rayleigh type p-Laplacian generalized neutral differential equation with variable parameter.Some new sufficient conditions for the existence of periodic solutions are obtained.The results have extended and improved the related results in the literatures.

periodic solution；Rayleigh type p-Laplacian equation；neutral operator；coincidence degree

O 175.12

A

1007-6883（2017）03-0008-07

责任编辑朱本华周春娟

2017-04-10

广东省高等教育教学改革项目（项目编号：GDJG20142396）；广东省高等学校教学团队建设项目（项目编号：粤教高函[2015]133号）；韩山师范学院理科团队项目（项目编号：LT201202）．

陈仕洲（1959-），男，广东汕头人，韩山师范学院数学与统计学院副教授.