基于数值模拟的大型原油储罐热辐射响应研究

赵金龙，黄弘，屈克思，苏伯尼



基于数值模拟的大型原油储罐热辐射响应研究

赵金龙，黄弘，屈克思，苏伯尼

(清华大学工程物理系，北京，100084)

为了得到一定热辐射条件下储罐的失效时间，对大型原油储罐在热辐射作用下的热响应进行研究，提出基于数值模拟的分析方法。利用FDS软件构建10万m³原油储罐燃烧模型，模拟得出邻罐所受到的热辐射强度分布；利用ANSYS软件构建10万m³原油储罐受热模型，分析储罐受到热辐射时的温度场分布；考虑储罐钢材的热物理性质，分析储罐在考虑热应力和不考虑热应力这2种条件下各自的失效时间。研究结果表明：考虑热应力时储罐经过245 s便发生失效，不考虑热应力时储罐理论失效时间超过3 600 s，可见大型原油储罐区火灾事故中热应力是储罐受热失效的关键因素。

大型原油储罐；ANSYS软件；FDS软件；热应力；失效时间

大型原油储罐(单罐容积大于5万m3)具有很多小型油罐不具备的优点，如单位容积占地面积小、耗费少、便于管理等，因此，油罐有朝着大型化、集约化发展的趋势[1−2]。对于大型罐区，储罐发生事故后，由于事件链效应，极易导致灾难性后果[3−5]。如2015−04−06，漳州古雷石化罐区大火，最初事故储罐先后引燃了临近2个储罐，大火持续了将近3 d，在救灾过程中导致6人受伤，被迫疏散周围29 096名群众，造成了巨大的经济损失和严重的社会影响[6]，因此，需研究在一定辐射强度下的储罐失效机理。10万m3原油储罐的直径达80 m，更大尺径的原油储罐也在不断地建造中。但进行全尺径储罐火灾实验一方面耗资巨大，另一方面可能带来严重的安全、环保问题，这些都限制了全尺径储罐火灾实验的可操作性。同时，从有限的火灾事故中得到的结果也不能满足人们的研究需要。随着计算机和有限元技术的不断进步和发展，构建储罐模型、利用先进的计算机数值模拟技术计算储罐燃烧过程中的各种特性参数是对储罐火灾研究的重要补充[7]。本文作者综合利用FDS和ANSYS等模拟分析软件，对10万m3原油储罐的全表面火灾燃烧特性进行研究，并在此基础上对邻近储罐受到的热辐射强度的分布、火灾环境中储罐的热响应情况及热应力分布等进行求解，进而获得储罐在一定火灾情境下的失效时间。

1 原油储罐的燃烧特性模拟

1.1 储罐的FDS模型

FDS是由美国标准与技术研究所建筑火灾研究实验室开发的火灾动力学模拟软件，通过燃烧模型、流体动力模型和热辐射模型解决火灾的模拟问题，适用于低马赫数的流场分析，模拟火灾以及烟气的发生、发展及蔓延过程[8]。

1.1.1 模型构建与网格划分

10万m3原油储罐的直径为80 m，高21.88 m，按照我国现行的GB 50074—2002“石油库设计规范”[9]，10万m3原油储罐间的防火间距为32 m。FDS中只能建立长方体结构的模块，因此，对圆形油罐采用多个长方体模块进行逼近模拟。模型如图1所示。

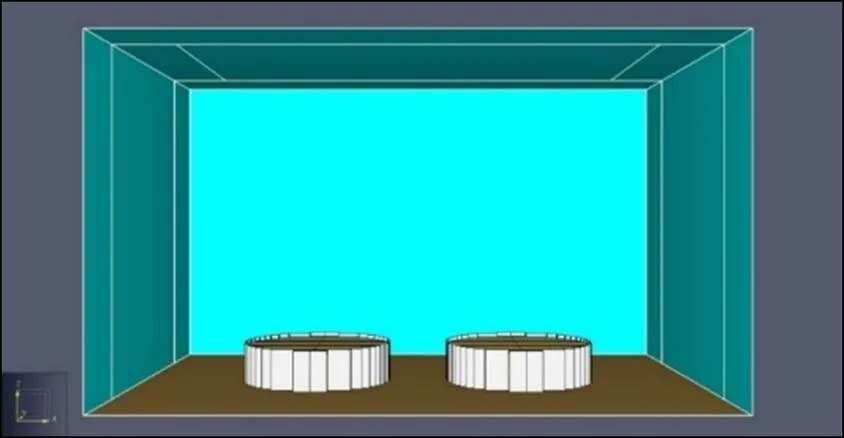
图1 10万m3 FDS储罐模型

本模拟采取多网格划分。根据FDS网格划分原则，对于2个储罐之间的区域，采用长、宽、高均为2 m的网格即可满足要求。对于其他的大空间，采取长、宽、高均为4 m的网格划分方式，网格数量总计423 000个。划分后网格如图2所示。

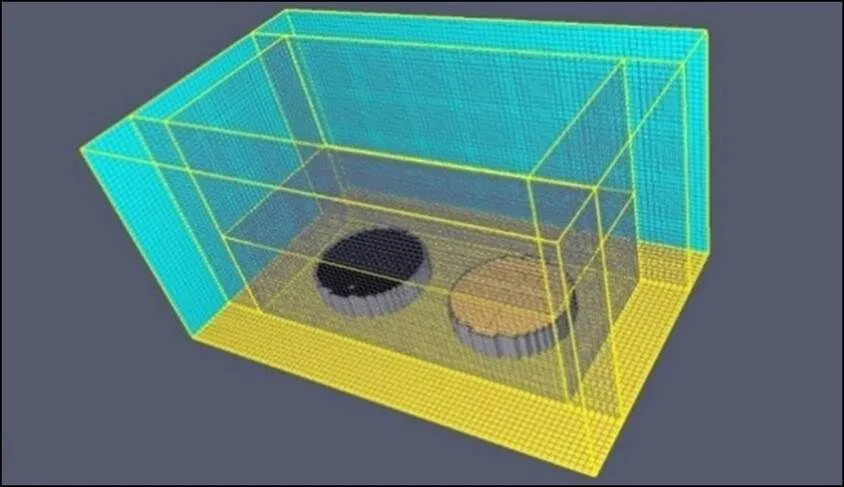
图2 划分完成的计算网格

1.1.2 燃料及火源设置

燃料与火源的关键参数设置如下。

1) 燃料的燃烧速率。根据相关实验研究，原油的燃烧线速度一般小于4 mm/min[10−11]。本模拟中使用的原油密度为890 kg/m3，质量燃烧速度选为0.059 kg/(m2∙s)。

2) 原油的热物理性质。原油属于混合物，不同产地的原油其热物性质相差很大，在实际工程中，要根据具体储存的原油品种进行选择。在本文中，参考文献[12−13]，选取的原油热物性参数如下：质量燃烧热为47 500 J/g；导热系数为0.15 W/(m·K)；比热容为2.4 kJ/(kg·K)；密度为890 kg/m3；最大质量燃烧速率为0.059 kg/(m2·s)。

1.1.3 热辐射探测器的设置

本模拟研究旨在原油储罐发生全表面火灾后，求解邻罐受到的热辐射强度分布。因此，在邻罐面向着火油罐一侧和整个浮顶表面设置热辐射通量探头。

由于油罐本身的对称性，探头只设置在油罐的半边，以减少运算量。其中，面向着火油罐的一侧，探头设置20列，每列间隔为2 m；每列探头自上而下为11个，每个间隔2 m；油罐的浮顶部分设置10组，每组间隔4 m，每组的探头间隔也为4 m，布置情况如图3所示。

在本次模拟中，共设置热辐射探测器376个。由于原油属于极易燃烧的高危物质，储罐被引燃后，油品表面火焰迅速蔓延，形成全表面火灾，并达到稳定。通过多次试验，将模拟时间设定为60 s即可满足需要。

1.2 FDS模拟储罐全表面火灾燃烧

按照1.1节中构建的模型、原型参数的设定和辐射探测器的布置，利用FDS进行模拟运算。运算完成后，对结果进行分析。

1.2.1 火焰的热释放速率

热释放速率HRR(heat release rate)是衡量燃料燃烧剧烈程度的重要指标，其物理意义是燃料在单位时间内燃烧释放的热量，单位为kW。HRR越大，表示燃烧得越剧烈，单位时间内释放的能量越多，对周围环境的影响就越大。图4所示为10万m3原油储罐满载时的HRR−时间曲线。

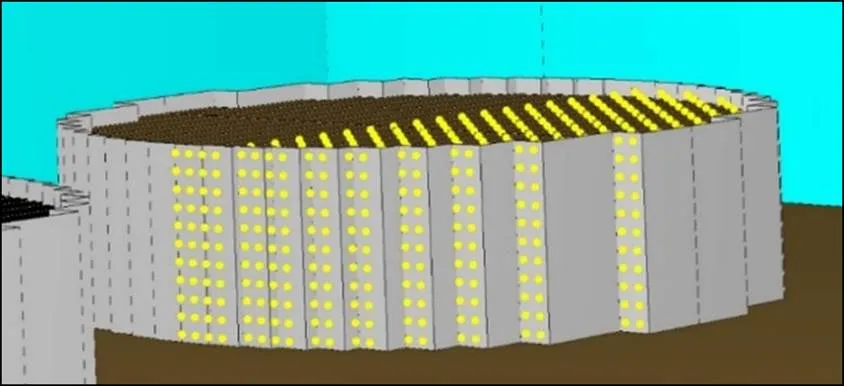
图3 布置好的热辐射探测器

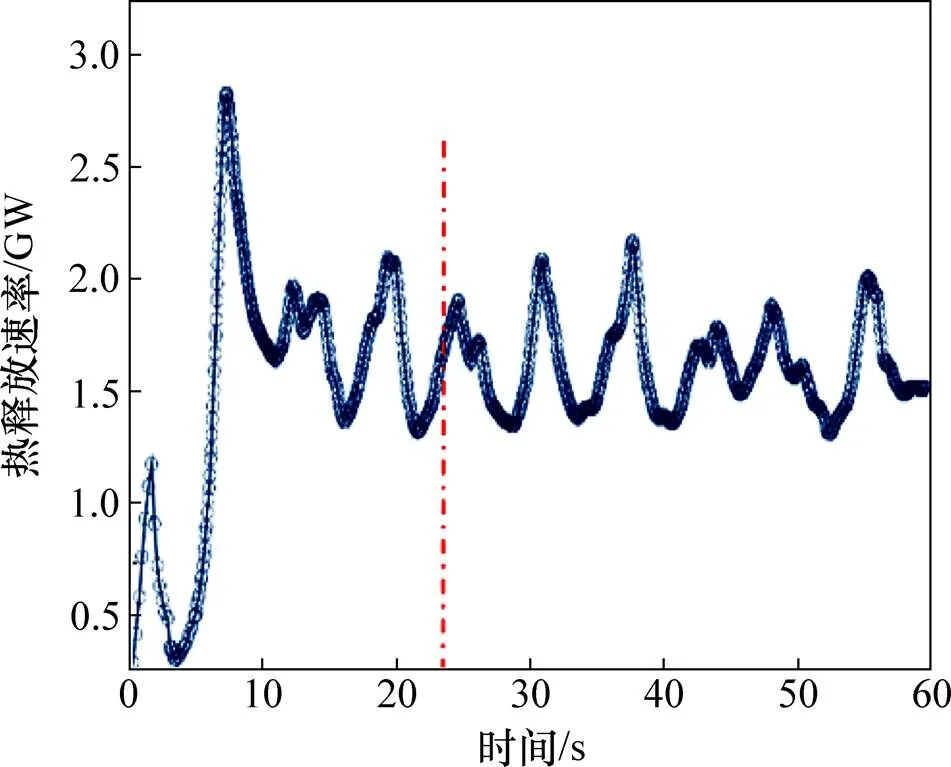
图4 满载时火焰的热释放速率−时间曲线

从图4可见：在23 s以后随着火焰的跃动，热释放速率起伏变化，但围绕1.5 GW波动，燃烧处于相对平稳状态。

1.2.2 相邻储罐受到的热辐射通量

热辐射通量的单位为kW/m2，表征热辐射强度。通过对探测器探测结果进行整理发现，邻罐所受到的热辐射通量在23 s以后趋于稳定，因此，选取23 s以后的热辐射通量平均值作为邻罐所受到的热辐射通量。图5所示为邻罐面朝着火油罐一侧所受到的热辐射通量的分布情况。从图5可以看出：在10万m3原油储罐发生全表面火灾时，相邻储罐的热辐射强度分布呈对称性分布，中间的黑色虚线即为对称轴；中间顶端强度最大，向下、向左右两边逐渐降低。

图6所示为相邻储罐的浮顶所受到的热辐射强度分布情况。

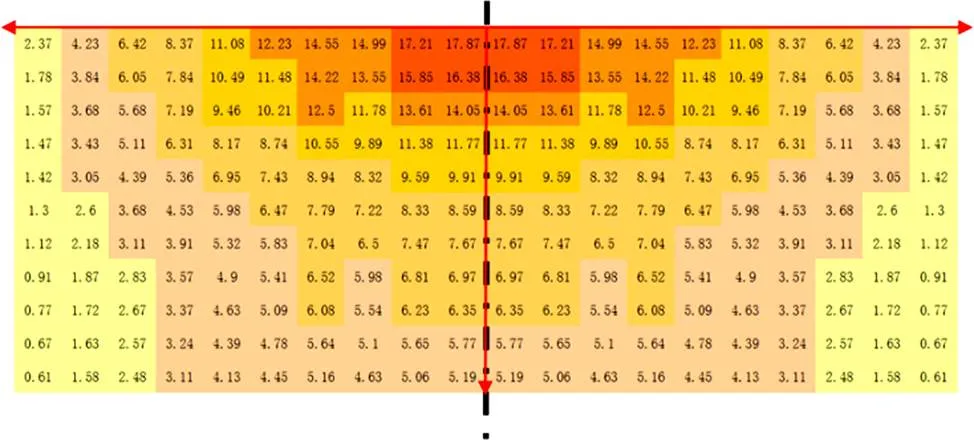
图中数据为热辐射强度，单位为kW/m2

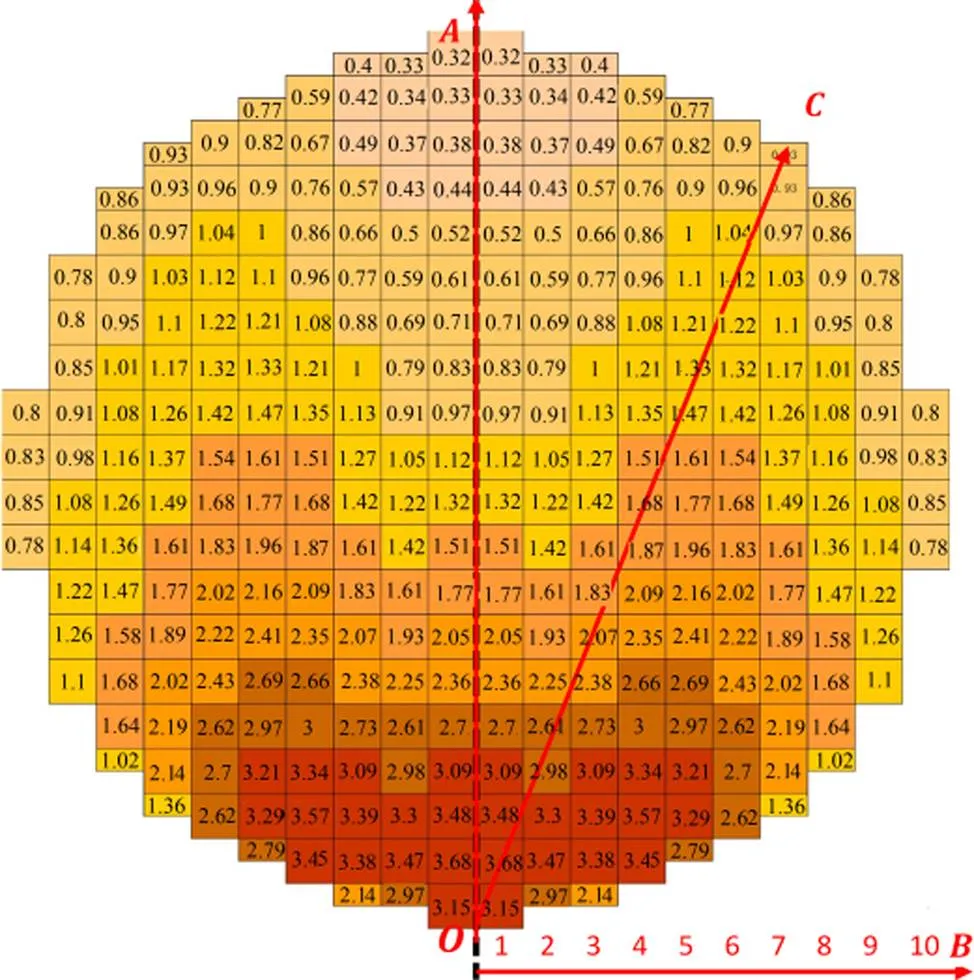
图中数据为热辐射强度，单位为kW/m2

从图6可看出：邻罐浮顶受到热辐射强度分布呈对称性分布；1~10号依次代表从中间往右边的10列探头，选择1，4，7和10共4列沿着方向对热辐射强度作图，如图7所示。

从图7可见：沿着方向箭头，浮顶受到的热辐射强度先上升而后逐渐降低。这是由于在靠近点处，距离壁板较近，壁板对热辐射的遮挡效应比较明显；随着距离增加，壁板的遮挡效应逐渐降低，热辐射强度逐渐增大，但之后随着与火焰之间的距离增加，热辐射强度开始减小。

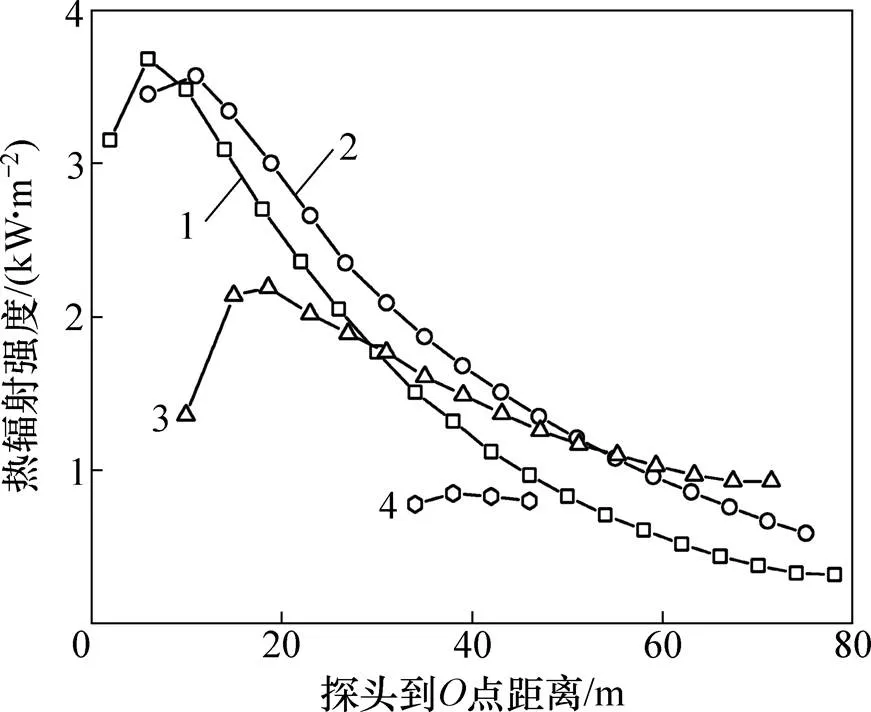
探头位置：1—第1列；2—第4列；3—第7列；4—第10列。

2 原油储罐热响应模拟

2.1 储罐的ANSYS软件模型

ANSYS软件由美国ANSYS公司开发，是目前使用范围最广的有限元分析软件，可以对结构、热、磁场等独立物理场问题及耦合物理场问题进行有限元分析。本文利用ANSYS Workbench平台构建10万m3原油储罐的三维模型，以模拟储罐受热后的热响应。

2.1.1 模型构建与网格划分

10万m3原油储罐直径为80 m，高度为21.88 m，上、下共9层，其中，第1~7层材料为日本进口钢材SPV490Q，第8层和第9层材料为国产钢材Q235A，各层的壁厚及高度见表1，储罐满载时储油高度为19.89 m。

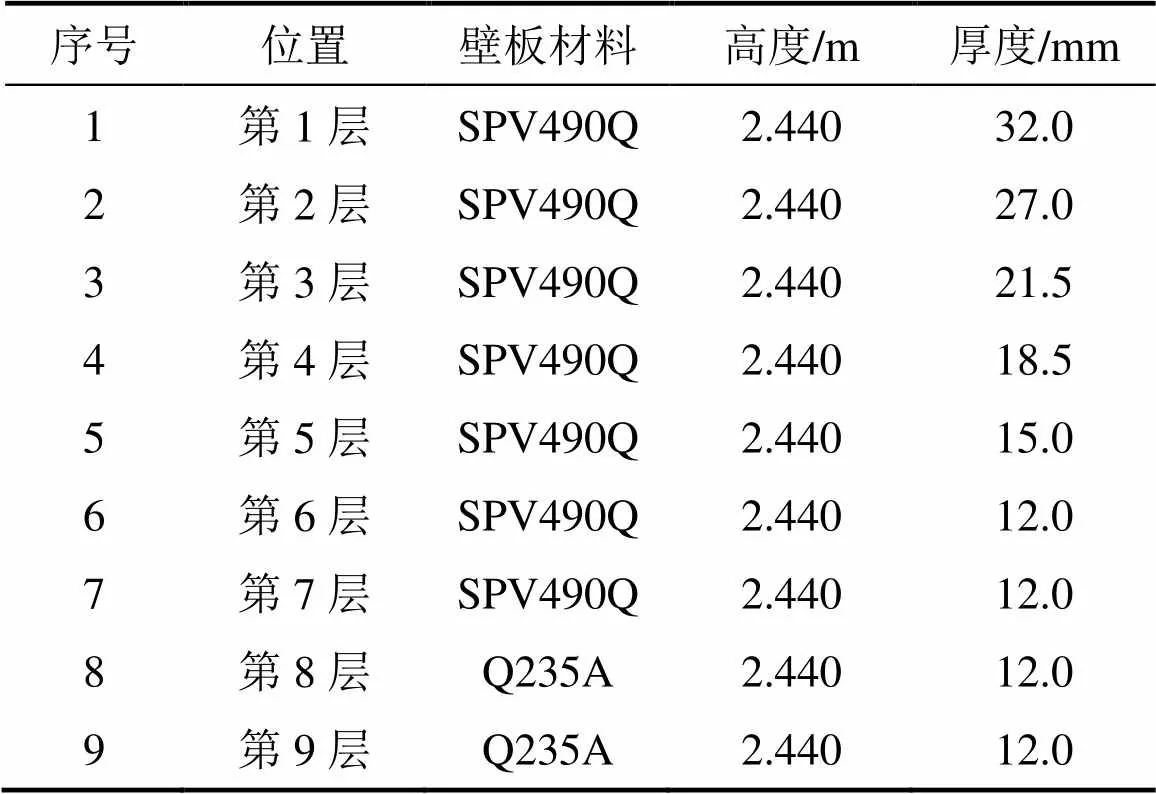
表1 10万m3储罐的结构、材料及尺寸

根据文献[14]，10万m3原油储罐的浮顶直径为 7 950 mm，高度为790 mm；浮顶为中空结构，上、下2层为4.5 mm厚钢板。考虑到对浮顶进行建模难度较大，在本模拟中，假设浮顶是1个圆柱体，且空气、浮顶以及浮顶下层的原油处于稳态传热状态，利用传热学原理求解其等效导热系数为0.022 9 W/(m∙K)。构建完成后的ANSYS模型如图8所示。根据文献[7]，得到模型中的材料及油品的物性参数如表2所示。

本模拟中，网格划分程序采用自动网格划分，对局部区域，通过Sizing方法，设定选定区域的单元边长或者设定选定边上的单元数目进行加密或调疏。划分完成后的网格侧视图及剖面图如图9所示，共计节点9 842个，单元3 322个。

图8 10万m3储罐的ANSYS三维模型

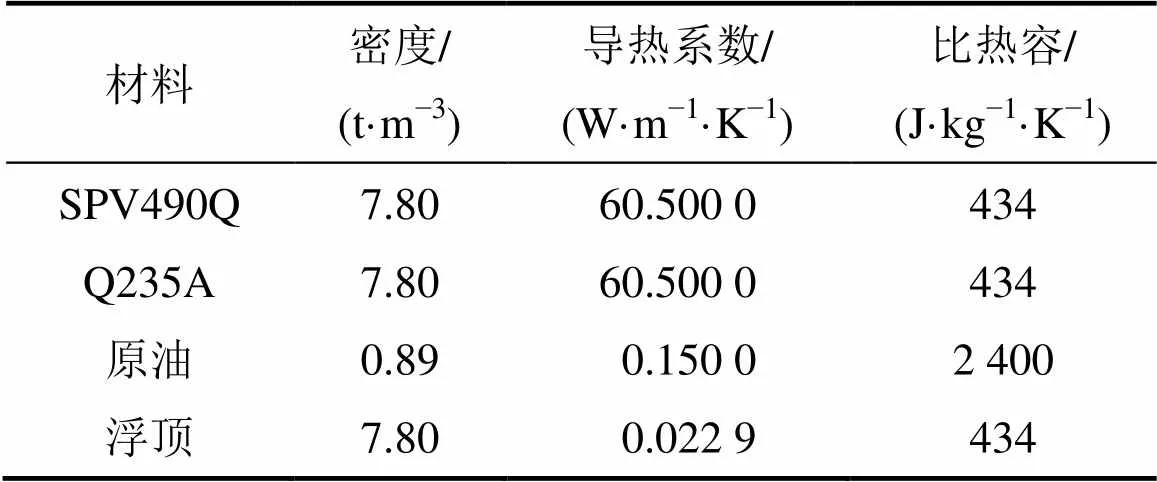
表2 储罐的热物性参数

图9 储罐模型的网格划分

2.1.2 载荷、边界条件的施加与求解

模拟中，原油储罐受到来自着火油罐的热辐射，将利用FDS软件求解得到的热辐射强度作为输入载荷，按照相应的区域划分，施加到对应的ANSYS模型上。油罐底部与基础承台相接，认为是完全绝热。据文献[15]，边界条件如下：

1) 储罐壁温度随着辐射时间增加逐渐升高，对所有的储罐壁面设置辐射边界条件，壁板的辐射发射率取为0.28；

2) 浮顶温度随着辐射时间增加逐渐升高，设定浮顶的辐射发射率为0.28；

3) 浮顶、储罐壁与空气之间存在对流换热，对流换热系数取为5 W/(m2∙K)。

为充分得到油罐受热后的热响应，设定求解时间为3 600 s。

2.2 储罐在热辐射作用下的温度场

通过ANSYS Workbench，对106m3原油储罐受热辐射时的温度场分布进行模拟。

2.2.1 储罐罐壁的温度分布

在热辐射作用下，受热3 600 s后储罐罐壁的温度场分布见图10。以储罐液面为分界线画1条黑色虚线，虚线上方的区域温度较高，温度最高的地方位于储罐罐壁中央顶部，最高温度为550 ℃；虚线下方的温度较低，不超过60 ℃。

在模拟中设定环境温度为20 ℃。注意到图10中出现低温18.431 ℃，低温点出现在接触单元不吻合之处，系ANSYS程序自动识别接触单元过程中发生的错误，这导致求解过程中局部不收敛。

临近储罐发生火灾后，朝向着火储罐一侧的罐壁温度变化较高，因此，本文选择朝向着火储罐的一侧进行分析研究。图10所示为罐壁的温度分布。

储罐内油品对于罐壁温度变化影响较大，为了直观反映罐壁不同位置的温度变化，提取3个重要的节点：罐壁顶端的点，设为点；紧邻液面上方的点，设为点；液面下方第一块壁板上的位置，设为点。观察它们的温度随时间的变化情况并得到这3个点的温度−时间变化关系曲线，如图11所示。从图11可以看出：

1) 热辐射作用3 600 s后，3个点的温度分别为549，274和39 ℃，相差很大。由于储罐内的大量油品充当了“吸热器”的作用，与油品接触的壁板可以很快将热量传递给油品，故点温度较低。

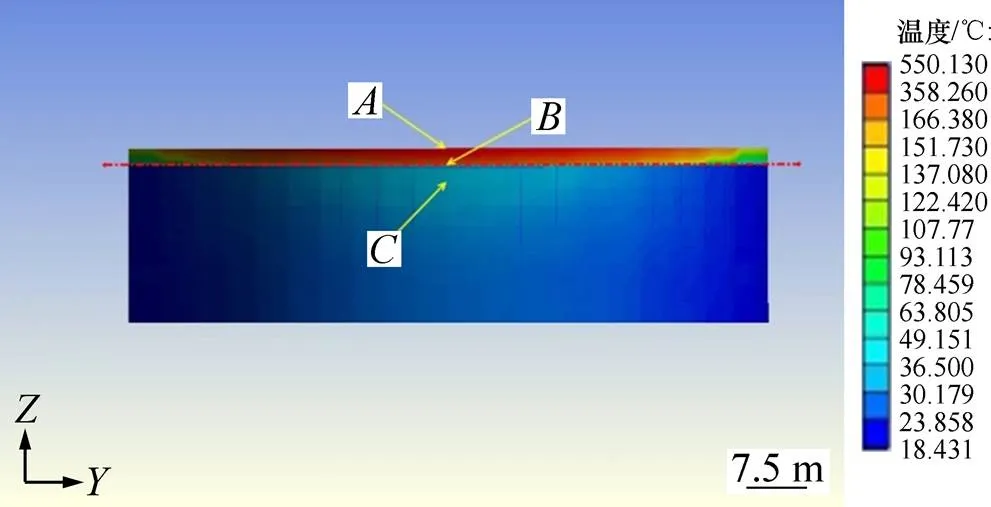
图10 邻罐罐壁的温度分布(3 600 s)

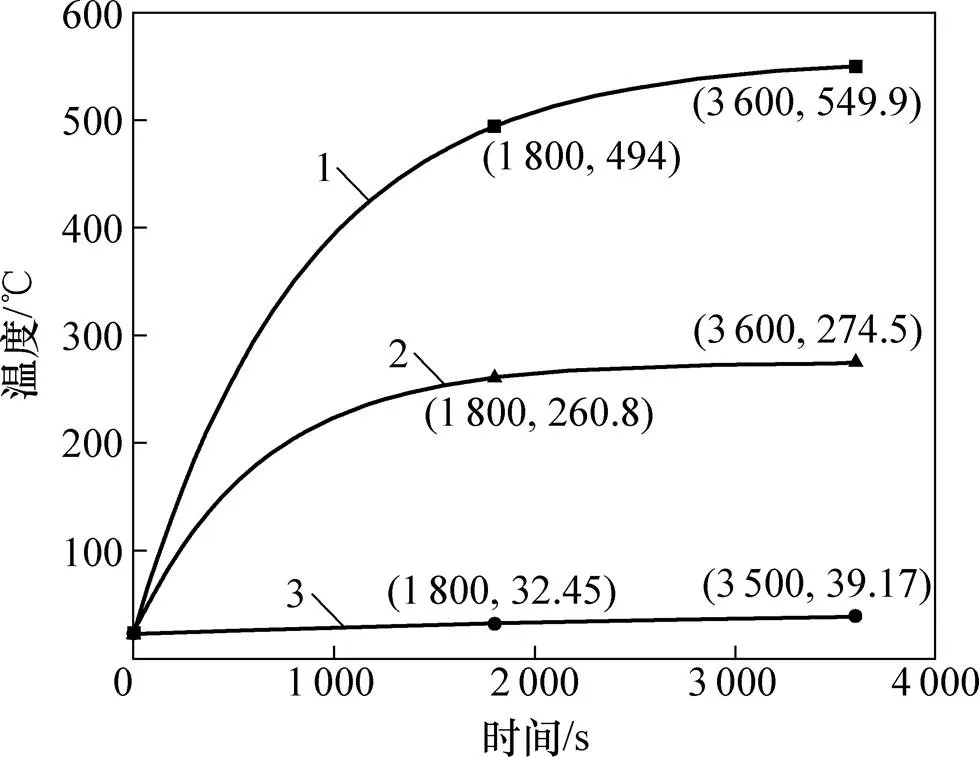
1—点A；2—点B；3—点C。

2)，和这3个点的温度都随着热辐射的作用逐渐增加，并且随着时间增加，温度增长的速度逐渐变小。如在1 800 s时，这3个点的温度分别达到494.00，260.00和32.45 ℃，分别占最大温度的90%，95%和83%，这表明随着时间增加，储罐接受到的辐射热量和储罐导出的热量逐步达到平衡。

2.2.2 储罐浮顶和罐内油品的温度分布

储罐的浮顶直接受到热辐射作用，温度升高；而罐内的油品则通过与储罐罐壁和浮顶发生热传导接收热量，温度升高。浮顶及罐内油品的温度分布如图12所示。

从图12可以看出：浮顶和罐内油品的温度分布与储罐受到的热辐射通量分布是一致的。

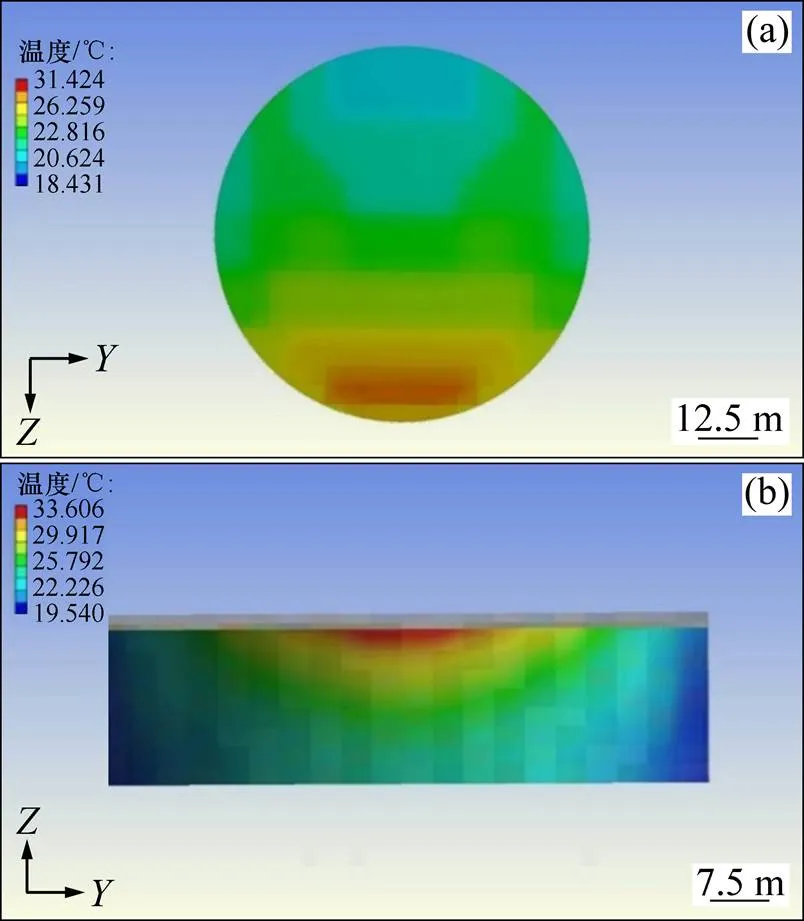
(a) 邻罐浮顶；(b) 罐内油品

3 10万m3原油储罐失效时间

在热作用下储罐壁的温度不断升高，对于钢材而言，其屈服强度随着温度升高不断下降，这有可能导致储罐壁板在热作用下发生内陷即应力失效。合理地预估热辐射作用下储罐壁发生应力失效的时间，对于消防安全、应急规划等具有重要意义。

3.1 储罐失效时间

COZZANI等[16−19]结合事故案例得出储罐失效的辐射阈值：对常压容器，在热辐射强度小于10 kW/m2时，设备的失效时间大于30 min；当热辐射强度小于15 kW/m2时，设备的失效时间大于10 min。这些阈值都是基于小型储罐(＜17 400 m3)得出的。对于大型储罐火灾，燃烧面积相对较大，邻罐接受到的热辐射增大，因此，上述结果对于大型储罐无疑很保守。杨国梁[20]认为，在没有任何防护措施时，钢设备发生热破坏的能量为20 MJ，据此得出在热辐射的作用下，原油储罐的上层罐壁发生应力失效的时间约为28 min。故在实际火灾场景下，大型储罐的失效时间需进一步研究。

欧洲钢结构协会(ECCS)根据大量的实验研究，给出了钢的屈服极限强度随温度的变化关系式：

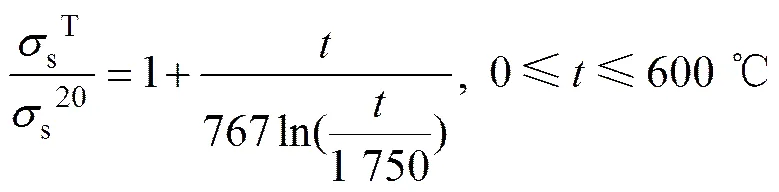
(2)

3.2 原油储罐失效时间

3.2.1 不考虑热应力时的储罐失效时间

在不考虑热应力时，认为储罐罐壁的应力状态不随温度发生改变；而罐壁材料的屈服强度则随着温度上升而降低。当罐壁某一点所受到的应力大于该点的屈服强度时，则认为储罐失效。

利用ANSYS APDL软件建立106m3原油储罐的轴对称模型，可求解得到储罐罐壁的von Mises等效应力，如图13所示。从图13可以看出：在储罐液面以上，罐壁所受的等效应力小于22 MPa。

结合图10和图13对数据进行分析计算得出：

1) 在储罐液面以下部分，储罐罐壁所受到的等效应力不超过钢材的许用应力；在受热后温度变化较小(小于60 ℃)时，屈服强度变化很小，不会发生失效。

2) 在储罐液面以上部分，罐壁钢材为Q235A，最高温度为550 ℃。此时，Q235A钢材的屈服极限强度为89.4 MPa。而由图13可知此时等效应力最大值约为22 MPa，没有超过此温度下的屈服极限强度，因此，不会发生失效。

上述结果是以储罐受热3 600 s即60 min计算的，事实上不可能预留这么长时间，使得储罐在完全无防护措施下受热。因此，在不考虑热应力时，储罐受到邻罐全表面火灾作用时不会发生应力失效。

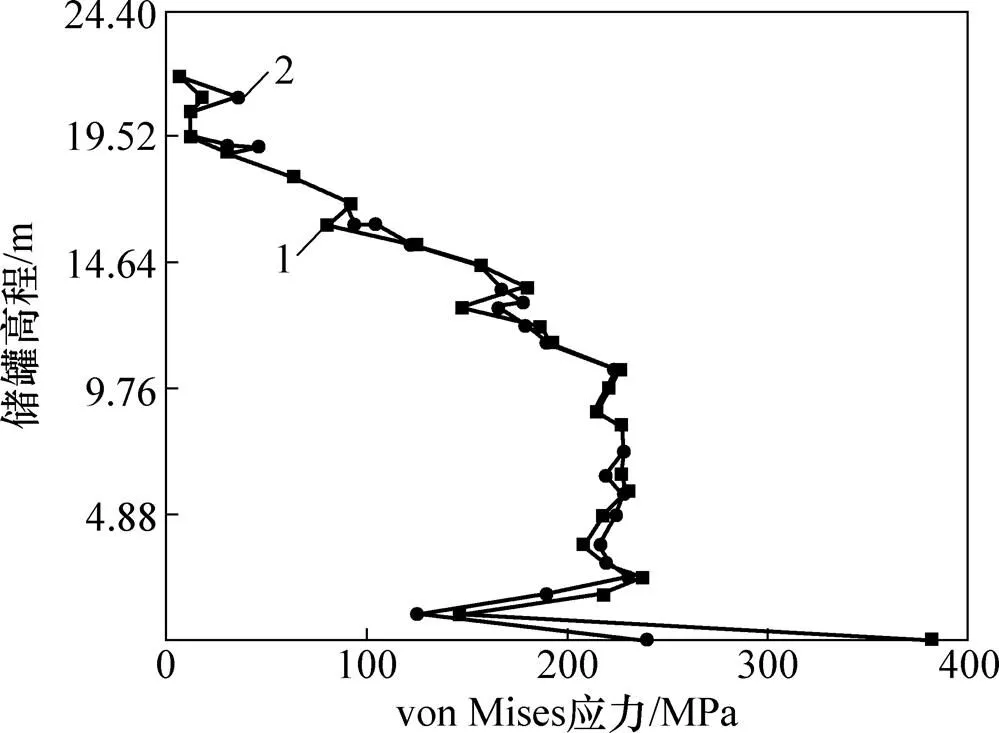
1—储罐内罐壁；2—储罐外罐壁。

3.2.2 考虑热应力时储罐失效时间分析

为求解储罐的热应力场分布，利用ANSYS Workbench耦合场分析方法，将受热时每1 s的温度分布作为载荷，导入ANSYS Static Structural分析中，设定总分析时间为600 s，求解温度载荷下的储罐应力分布，所得结果如图14所示。

图14 温度场作用下的储罐应力场分布

如图14可见：在600 s时，储罐罐壁的应力场最大值达421 MPa，远远超过Q235A的屈服强度。为此，从图14中提取应力值最大的节点，导出该节点的应力随时间变化的情况，结合节点温度和屈服极限随时间变化的曲线求解得到储罐的失效时间，如图15所示。

从图15可见：在0~600 s范围内，随着时间增加，节点温度随之增大，在20~185 ℃之间变化；屈服强度随着温度升高而降低，但降低幅度很小，在233~209 MPa之间变化；节点的应力变化范围为171~421 MPa。

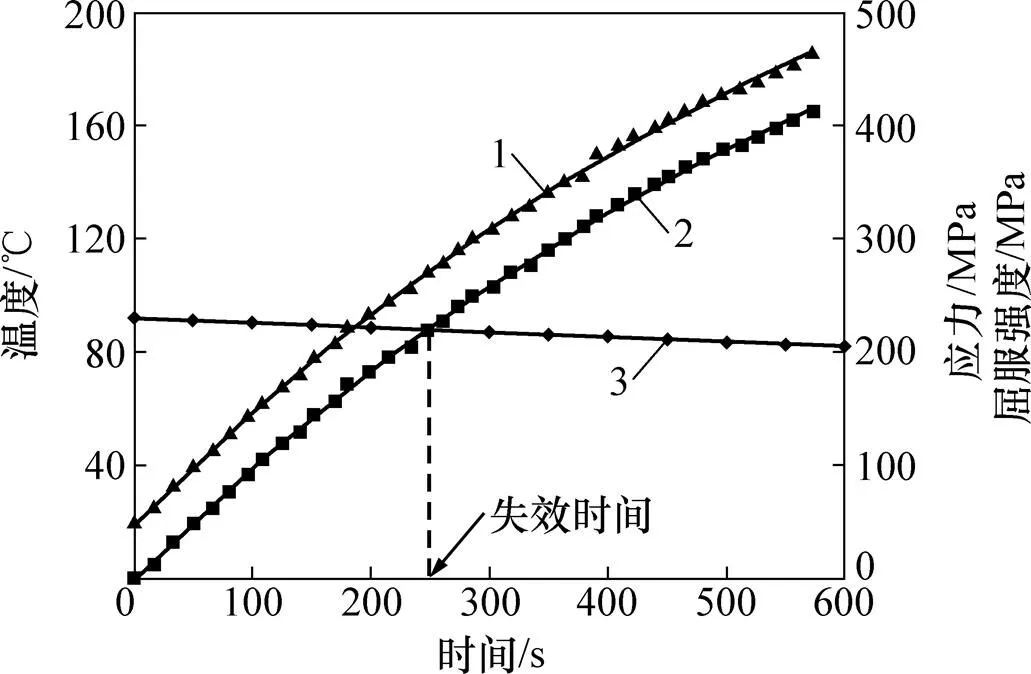
1—节点温度；2—节点应力；3—节点屈服强度。

可见，钢材屈服极限强度随温度变化的范围很小，对整体应力的影响并不大；而由于钢材的热膨胀导致结构热应力很大，对罐体的应力分布起到决定性作用。从图15可见：应力变化曲线与屈服极限变化的曲线的交点为，即为罐壁发生失效的时间点；失效时间约为245 s。

4 结论

1) 利用FDS软件对106m3原油储罐发生的全表面火灾进行模拟，得到相邻储罐受到的热辐射强度的分布。

2) 利用ANSYS Workbench软件研究热辐射作用下原油储罐的热响应情况，得到储罐受热后的温度场分布。

3) 热应力在储罐失效过程中起决定性作用，求解得到10万m3的原油储罐在发生全表面火灾情况下，邻罐的失效时间为245 s。

基于本文的研究，下一步的研究方向有2个：

1) 本文中求解温度场及热应力场时，为了减小计算量，网格数目偏少，所得结果精度有限。如何划分更合理的网格是下一步研究的重点。

2) 在求解热应力场时，没有考虑原油储罐库中的各种消防措施，得到的失效时间比较保守。需在本文研究基础上考虑有效救援时间等，建立储罐事故的多米诺效应扩展概率模型。

[1] SHUAI Jia, HAN Kejiang, XU Xuerui. Risk-based inspection for large-scale crude oil tanks[J]. Journal of Loss Prevention in the Process Industries, 2012, 25(1): 166−175.

[2] SHEBEKO Y N, BOLODIAN I A, MOLCHANOV V P, et al. Fire and explosion risk assessment for large-scale oil export terminal[J]. Journal of Loss Prevention in the Process Industries, 2007, 20(4): 651−658.

[3] 赵金龙, 唐卿, 黄弘, 等. 基于数值模拟的大型外浮顶储罐区定量风险评估[J]. 清华大学学报(自然科学版), 2015, 55(10): 1143−1149. ZHAO Jinlong, TANG Qing, HUANG Hong, et al. The quantitative risk assessment of the external floating roof tank areas based on the numerical simulation[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(10): 1143−1149.

[4] ZHAO Jinlong, HUANG Hong, SU Boni, et al. The quantitative risk assessment of the storage tank areas based on the domino effect[C]/LEE L. Civil Engineering and Urban Planning IV (CEUP). Beijing, China, 2016: 65−69.

[5] COZZANI V, GUBINELLI G, ANTONIONI G, et al. The assessment of risk caused by domino effect in quantitative area risk analysis[J]. Journal of Hazardous Materials, 2005, 127(1): 14−30.

[6] NI Zijian, WANG Yanzhuang, YIN Zhigang. Relative risk model for assessing domino effect in chemical process industry[J]. Safety Science, 2016, 87: 156−166.

[7] WU G X, MA Q W, TAYLOR R E. Numerical simulation of sloshing waves in a 3D tank based on a finite element method[J]. Applied Ocean Research, 1998, 20(6): 337−355.

[8] KEVIN M, SIMO H, RANDALL M, et al. Fire dynamic simulator technical reference guide[M]. USA: National Institute of Standards and Technology Special Publication, 2013: 1−3.

[9] GB 50074—2002, 石油库设计规范[S]. GB 50074—2002, Code for design of oil depot[S].

[10] BABRAUSKAS V. Estimating large pool fire burning rates[J]. Fire Technology, 1983, 19(4): 251−261.

[11] KOSEKI H, NATSUME Y, IWATA Y, et al. Large-scale boilover experiments using crude oil[J]. Fire Safety Journal, 2006, 41(7): 529−535.

[12] McGRATTAN K B, BAUM H R, HAMINS A. Thermal radiation from large pool fires[R]. Gaithersburg, USA, 2000: 1−20.

[13] HURLEY M J, GOTTUK D T, JIR J R H, et al. The SFPE handbook of fire protection engineering[M]. Quincy, MA, USA, 2002: 560−572.

[14] 王善忠. 十万立方米原油储罐的设计[D]. 天津: 天津大学化工学院, 2007: 4−5. WANG Shanzhong. The design of 100 000 m3oil tank[D]. Tianjin: Tianjin University Institute of Chemical Industry, 2007: 4−5.

[15] BERGMAN T L, INCROPERA F P, LAVINE A S. Fundamentals of heat and mass transfer[M]. New Jersey, USA: John Wiley & Sons, 2011: 669−723.

[16] COZZANI V, ZANELLI S. An approach to the assessment of domino accidents hazard in quantitative area risk analysis[C]// Loss Prevention and Safety Promotion in the Process Industries. Amsterdam: Elsevier, 2001: 1263−1274.

[17] COZZANI V, GUBINELLI G, ANTONIONI G, et al. The assessment of risk caused by domino effect in quantitative area risk analysis[J]. Journal of Hazardous Materials, 2005, 127(1): 14−30.

[18] COZZANI V, GUBINELLI G, SALZANO E. Escalation thresholds in the assessment of domino accidental events[J]. Journal of Hazardous Materials, 2006, 129(1): 1−21.

[19] LANDUCCI G, GUBINELLI G, ANTONIONI G, et al. The assessment of the damage probability of storage tanks in domino events triggered by fire[J]. Accident Analysis & Prevention, 2009, 41(6): 1206−1215.

[20] 杨国梁. 基于风险的大型原油储罐防火间距研究[D]. 北京: 中国矿业大学(北京)资源与安全工程学院, 2013: 67−68. YANG Guoliang. Study of minimum shell-to-shell spacing of large petroleum storage tanks based on risk[D]. Beijing: China University of Mining and Technology (Beijing). Faculty of Resources & Safety Engineering, 2013: 67−68.

(编辑 陈灿华)

Research on thermal radiation response of large crude oil tank based on numerical simulation method

ZHAO Jinlong, HUANG Hong, QU Kesi, SU Boni

(Department of Engineering Physics, Tsinghua University, Beijing 100084, China)

A numerical simulation method on the thermal radiation response of a large-scale crude oil tank was presented to determine the failure time under the attack of thermal radiation. A 106m3crude oil tank was established by FDS software to simulate fire and the distribution of thermal radiation for an adjacent tank was obtained. After that, a 106m3crude oil tank was established with the ANSYS software and the temperature distribution of the tank was obtained under the thermal radiation impact. Combined with the physics properties of the tank steel, the failure time of the oil tank was calculated in two conditions, including the thermal stress and excluding the thermal stress. The results show that the oil tank would fail in 245 s considering the thermal stress, while the failure time exceeds 3 600 s without considering the thermal stress, which indicates that the thermal stress is the key factor in the process of tank failure under thermal conditions.

large crude oil tank; ANSYS software; FDS software; thermal stress; time to failure

10.11817/j.issn.1672−7207.2017.06.032

X937

A

1672−7207(2017)06−1651−08

2016−07−23；

2016−09−13

重大科技支撑计划项目(2015BAK12B01)；国家重点研发计划项目(2016YFC0802501)；化学品安全控制国家重点实验室基金资助项目(2016)(Project(2015BAK12B01) sponsored by the Ministry of Science and Technology of the People’s Republic of China; Project(2016YFC0802501) supported by National Key Research and Development Plan; Project(2016) supported by the State Key Laboratory of Safety and Control for Chemicals)

黄弘，博士，教授，从事城市公共安全研究和化工园区定量风险评估等研究；E-mail：hhong@mail.tsinghua.edu.cn