基于多分布响应面算法的火炮方向机齿轮传动误差可靠性分析
2017-07-20白亚莉刘文强
白亚莉 张 毅 冀 敏 刘文强
1.西京学院机械工程学院,西安,710123 2.西京学院机电技术系,西安,7101233.西京学院数学系,西安,710123
基于多分布响应面算法的火炮方向机齿轮传动误差可靠性分析
白亚莉1张 毅1冀 敏2刘文强3
1.西京学院机械工程学院,西安,710123 2.西京学院机电技术系,西安,7101233.西京学院数学系,西安,710123
为了提高火炮方向机齿轮传动误差(GTESMG)的分析效率并考虑工程设计可行性,提出了一种改进的多分布协作响应面算法(MDCRSA)。该算法从概率的角度出发,综合考虑静态影响因素和动态影响因素,结合响应面法和蒙特卡罗法,评估系统可靠性。将该算法应用到实际项目中估算GTESMG的可靠性,结果显示:当GTESMG的设计值为10′时,估算的可靠度为0.990,基本上满足GTESMG的设计和工程需要。同时通过与传统估计可靠性方法的比较,可以看出MDCRSA算法具有较高的计算效率及精度,并且这种优势随着计算次数的增加而更加明显。MDCRSA算法不仅可以评估GTESMG可靠性,还可预测火炮其他部件的可靠性。
火炮方向机;传动误差;可靠性;多对象多因素;多分布协作响应面算法
0 引言
火炮方向机齿轮传动误差(gear transmission errors of the steering mechanism of the gun,GTESMG)直接影响火炮方向机(steering mechanism of the gun, SMG)的工作性能、效率、精度和寿命[1-2]。目前,关于火炮转向装置传动误差的可靠性理论与实验研究还鲜有报道。火炮方向机的结构设计与工作环境非常复杂[3-5],文献[6-10]对火炮方向机设计过程中的确定性设计进行了研究,但没有考虑SMG的其他重要影响因素以及部分因素的随机性。实际上,由于GTESMG所涉及的大多数影响因素是时变的,故上述研究在工程使用方面局限性很大。由此可见,只有在设计过程中考虑各种确定性因素以及随机性因素,才可以客观和准确地描述GTESMG的可靠性。本文所讨论的GTESMG由确定性因素确定的静态误差和随机因素确定的动态误差决定,因此,本文从这两个方面分析研究GTESMG的可靠性。
概率分析法被广泛应用在许多领域的可靠性分析中,文献[11]在水利、材料领域的误差分析中利用概率分析法得出了更加精确的结果;文献[12]应用概率方法分析飞行误差;文献[13]应用概率法分析机械灵敏度动态误差。响应面法(RSM)通过一系列确定性实验,用多项式函数来近似表示隐式极限状态函数。蒙特卡罗法(MCM)以概率和统计为基础,将所求解的问题同一定的概率模型相联系,实现统计模拟或抽样,从而获得问题的近似解。
由于GTESMG很复杂,故仅使用一种方法分析难以实现,并且直接使用RSM或MCM,因计算过程繁琐,估算结果的精度难以保证,也难以实际应用。为了解决上述问题,本文针对GTESMG提出了基于RSM和MCM的多分布式协作响应面算法(MDCRSA)。这种算法不仅解决了传统算法耗时长、结果不精确等问题,而且将火炮这种复杂部件依性质分类,由繁化简,符合实际设计与分析流程。本文基于实际项目,综合分析影响GTESMG可靠性的确定性因素和随机因素,并以此结果来验证MDCRSA算法的有效性。
1 基于MDCRSA算法的可靠性分析
1.1 MDCRSA算法的原理
假设系统输出响应为Y,输入变量为X,则二次响应面函数[13]为
Y(X)=ao+BX+XTCX
(1)
其中,ao、B和C分别为常数项、线性系数矩阵和二次系数矩阵。为了有效预测GTESMG的可靠性,通过对SMG结构可靠性的研究,本文基于RSM和MCM提出了MDCRSA算法。MDCRSA算法可用于预测由多个零件(本文中称为对象)组成的部件的可靠性。MDCRSA算法基本理论如下:
(1)基于结构和功能把复杂的多对象多因素模型分成几个单对象单因素部分,并根据每个对象因素的特性和实际情况以适当方式对单对象单因素部分进行RSM分析,应用式(1),获得相应的输出响应。
(2) 使用MDCRSA算法分析可靠性。将获得的单对象单因素的输出响应作为下一步分析的输入变量,再次使用响应面公式,得到输出响应。再将此输出响应作为总体的输入变量进行总输出,得出这个部件的可靠性模型。
通过分解、合并的分析方式将复杂问题简单化,以适应实际工程项目的设计流程,这样更易于操作且更加精确。相对于传统GTESMG中的可靠性估算方法,MDCRSA方法在思路上有了进一步的创新,不是简单的材料刚强度校验,而是从结果出发,以精确的影响因素数据为基础计算可靠度,结果更加直观。
1.2 MDCRSA算法的数学模型
基于式(1)的二次响应面方程建立MDCRSA的基本数学模型,假设GTESMG包括m(m∈Z)个对象,每个对象与n(n∈Z)个因素相关,令输入变量为Xij(Xij指第i个对象的第j个因素),对应的输出响应是Yij,则得到响应面函数以及它们之间的关系:
Yij=f(Xij)i=1,2,…,m;j=1,2,…,n
(2)
(3)
Bij=B1,ijB2,ij…Bk,ij
(4)
(5)
Xij=[x1,ijx2,ij…xk,ij]T
(6)
其中,ao、B和C都是未知参数,k是变量的个数。单对象多因素Xi作为响应面的输入变量,则输出响应Yij公式如下:
(7)
Yij中i是单对象多因素Xi的输出响应,具体表示如下:
(8)
由此可知,当所有对象的输出响应被看作输入变量,表达式如下:
(9)
则总的输出响应
(10)
式(10)就是多分布协作响应面公式。ao、B和C是响应面公式的常系数。式(3)、式(8)、式(10)三个公式原理相同,将总的响应面模型分解为多个单对象单因素响应面模型后,依次以前一次得到的输出响应作为输入变量得出下一步的输出响应,重复此步骤,直到得出整体的响应面结果,进而得出可靠性结果。
2 基于MDCRSA的GTESMG可靠性分
析步骤
由图1可以看出,方向机由3对齿轮副和4个齿轮轴组成(忽略轴承等小标准件),每个对象涉及多个影响因素,需依次分析各因素对整个系统的影响。结合前文所述的MDCRSA可靠性分析原理可得GTESMG的MDCRSA可靠性分析流程,如图2所示。

(a)SMG结构三维图

(b)SMG传动系统图图1 SMG结构及其传动系统Fig.1 Structure and transmission system of SMG

图2 GTESMG的MDCRSA可靠性设计的流程图Fig.2 Flow chart of GTESMG reliability analysis based on DCRSM
(1)将误差分为静态误差和动态误差两类,用适当的方法分析不同类型误差。当炮塔的角加速度从0°/s2变到70°/s2时(此过程作为一个任务剖面),8个临界点的动态负载载荷谱如图3所示。

图3 齿轮所受法向力与载荷谱Fig.3 Normal force on gears and the load spectrum of shafts
(2)根据载荷变化分析误差。画出不同角加速度下误差的拟合曲线,找出误差最大值点(危险点),以此作为可靠性分析的参考。
(3)以上述危险点作为参考点,列极限方程求解,估算该系统的可靠度,从而确定系统可靠性。
(4)对MDCRSA分析结果的有效性进行验证。
上述前两个步骤与第1节所述相似,有效性验证主要通过与传统计算方法相比较来实现。下文阐述第三步中极限方程的确定方法。
假设SMG的系统误差为δΣ,静态误差为δΣ1,动态误差为δΣ2,由主动轴的扭曲变形造成的传动误差为γΣ,由驱动轴的弯曲变形引起的误差为χΣ,由齿轮扭曲变形造成的传动误差为φΣ,它们之间的关系式为[13]
δΣ2=γΣ+χΣ+φΣ
(11)
δΣ=δΣ1+δΣ2=δΣ1+γΣ+χΣ+φΣ
(12)
根据《火炮设计手册》,SMG的可靠性随负荷(转子速度)而变化的极限状态函数为Y(ω)[14],当SMG的允许误差为δ时,有
Y(ω)=δΣ(ω)+χΣ(ω)+φΣ(ω)-δ
(13)
GTESMG达到可靠要求的边界条件为Y(ω)<0。假设每个变量之间是相互独立的,那么它们的均值和方差矩阵分别为
μ=[μδΣ1μγΣμχΣμφΣ]
σ=[σδΣ1σγΣσχΣσφΣ]
由文献[12]可得误差Y的均值与方差:
E(Y)=
μY(μδΣ1,μγΣ,μχΣ,μφΣ,μδΣ1,μγΣ,μχΣ,μφΣ)
(14)
D(Y)=
DY(μδΣ1,μγΣ,μχΣ,μφΣ,μδΣ1,μγΣ,μχΣ,μφΣ)
(15)
式中,μY(·)为均值函数;DY(·)为方差函数。
整个GTESMG的可靠性指标β以及可靠度R分别为[15]
(16)
3 GTESMG可靠性分析
3.1 GTESMG分析
齿轮传动误差分解为静态误差和动态误差。静态误差的重要来源是制造误差和安装误差。制造误差主要由几何离心率、运动偏心、齿形误差以及齿宽偏差引起;安装误差由实际旋转中心和理论旋转中心的偏差引起,主要是轴和齿轮的配合间隙、轴承的径向间隙以及中心距偏差导致。动态误差是由扭矩的变化、材料本身的缺陷导致的弹性变形引起的,主要包括传动轴扭曲变形、传动轴弯曲变形以及齿轮扭转变形引起的传动误差。
根据误差计算原则[10],得到角加速度为70°/s2时两种类型的传动误差[10]。静态误差结果如表1所示,动态误差结果如表2~表4所示。表中,Z2/Z1表示Z2、Z1齿轮传动副,其他类推;Jt表示圆周侧隙;d2为从动轮分度圆直径;Ψ为单向传动误差角;φ为空回误差角;χa为齿顶圆位移;χf为齿根圆位移;η为分度圆位移;φ为扭转变形角。

表1 SMG的静态误差

表2 传动轴扭曲变形引起的传动误差

表3 传动轴弯曲变形引起的传动误差
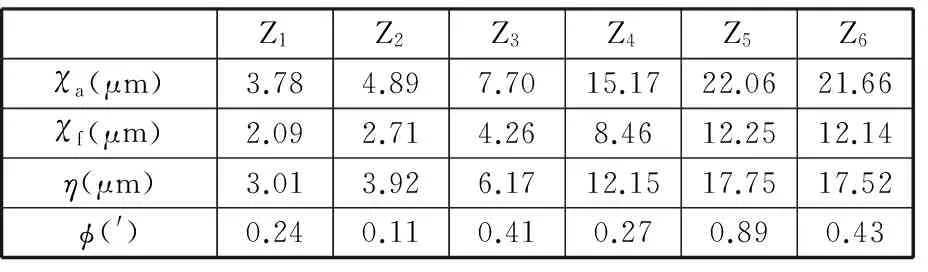
表4 齿轮扭转变形引起的传动误差
3.2 随机变量的选择
为了验证SMG的MDCRSA可靠性分析效果,根据实际情况,设定SMG中某些重要参数(参考工程经验,选择角加速度为70°/s2时的参数)为随机变量,如齿轮模数m、材料密度ρ、齿面法向力Fn、压力角α、扭矩T,如表5所示。这些参数相互独立且分别服从正态分布。
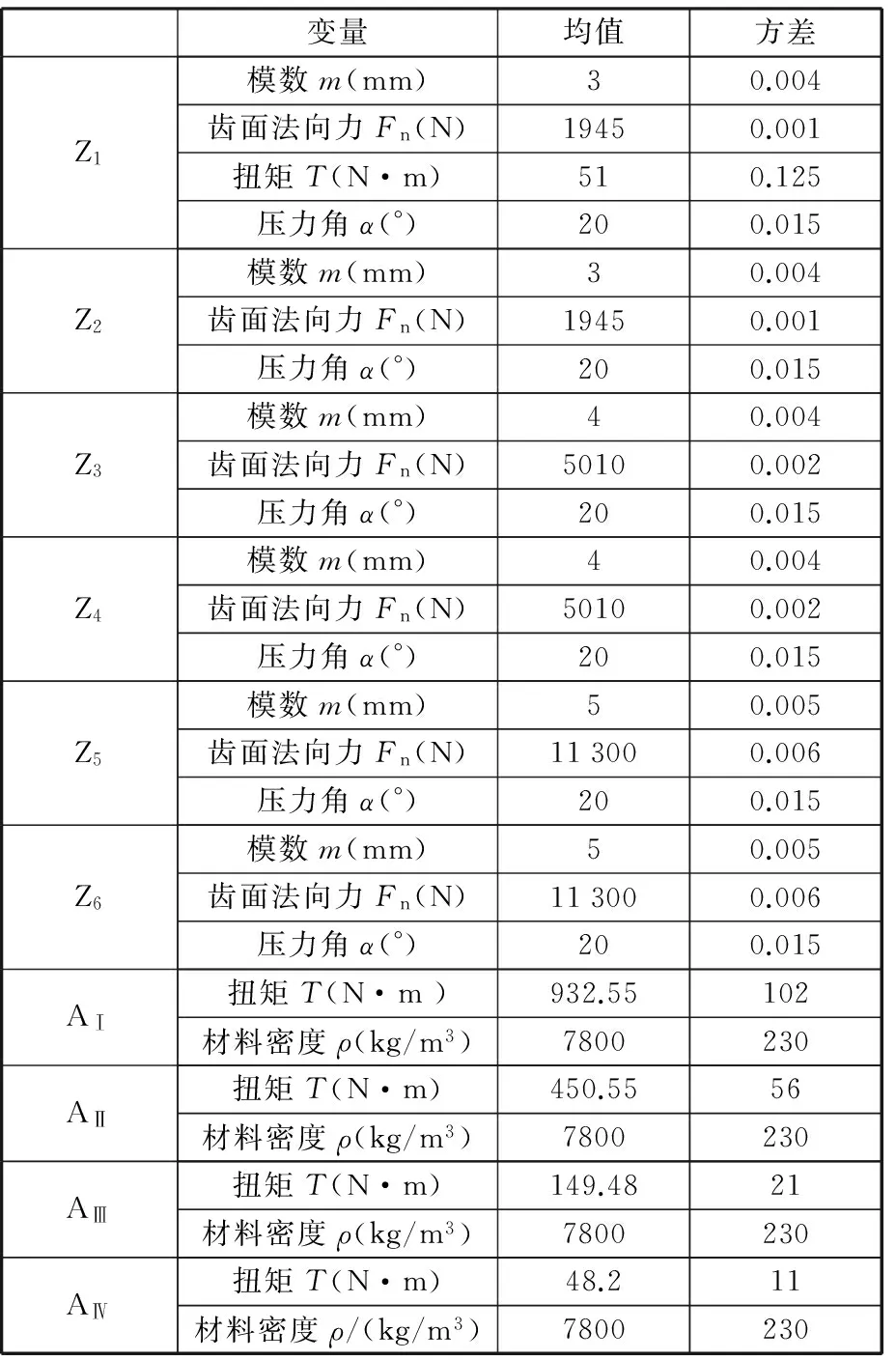
表5 GTESMG (角加速度70°/s2)的随机变量选择
3.3 齿轮传动误差危险点的确定
角加速度随负载的变化而变化,所以火炮方向机的传动误差随负载改变。在一个任务剖面内,不同的传动误差可以通过相同的方法计算。假设静态误差是3.18 mm(数据来源于《火炮设计手册》),可以模拟得出随角加速度不同,火炮方向机传动误差的变化曲线,如图4所示。

图4 SMG不同角加速度下的传动误差的曲线拟合Fig.4 Fitting curves of transmission errors of SMG with different rotor speed
由图4可以看出,在一个任务剖面内,火炮方向机齿轮传动误差Y几乎是呈线性增加的,因此,可靠性危险点将在最大负载时获得,即角加速为70°/s2时得到。该点的误差应该被视为GTESMG可靠性分析的计算点,当此点的安全性可以保证时,整体的可靠性即可保证。
3.4 可靠性分析
3.4.1 单个对象的可靠性分析
对于单个对象,根据随机因素(表5)的随机取值变化来模拟响应面模型10 000次,得出单个对象在随机变化下随机误差的输出响应值的直方图。所有输出响应均服从正态分布[10],得出SMG的动态误差。传动轴扭曲变形、传动轴弯曲变形、齿轮扭转变形引起的三种动态误差的平均值分别为3.1725′、5.2891′、0.1539′,标准差分别为0.0135′、0.0022′、0.1002′,服从正态分布。根据表5中所列齿轮变量的均值和方差,将齿轮随机变量的统计特性分别输入各自的有限元模型,并分别进行有限元分析(20、38),(22、45),(25、40)次,各齿轮的有限元分析如图5~图10所示。由Box-Behnken矩阵法获得测试样本,并用6个齿轮的响应面模型代替各自的有限元分析模型,再应用MCM法对每个响应面模型进行10000次的抽样实验,对得到的数据进行分析,得到各齿轮的输出响应直方图,如图11~图16所示。显而易见,所有的输出响应服从正态分布,且各自的平均值分别为0.247′、0.009′、0.408′、0.268′、 0.896′、0.430′,标准偏差分别为0.0205′、0.0211′、0.0182′、0.0185′、0.0211′、0.0128′。

图5 齿轮Z1受力变形有限元分析Fig.5 Load-deformation diagrams of gears Z1
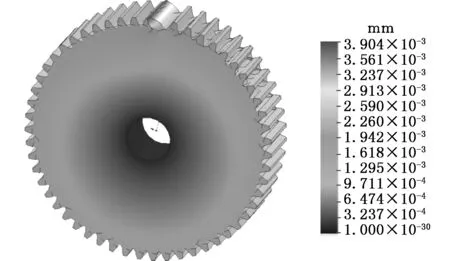
图6 齿轮Z2受力变形有限元分析Fig.6 Load-deformation diagrams of gears Z2

图7 齿轮Z3受力变形有限元分析Fig.7 Load-deformation diagrams of gears Z3

图8 齿轮Z4受力变形有限元分析Fig.8 Load-deformation diagrams of gears Z4

图9 齿轮Z5受力变形有限元分析Fig.9 Load-deformation diagrams of gears Z5

图10 齿轮Z6受力变形有限元分析Fig.10 Load-deformation diagrams of gears Z6

图11 齿轮Z1的误差分布直方图Fig.11 Total error maps of each gear Z1

图12 齿轮Z2的误差分布直方图Fig.12 Total error maps of each gear Z2
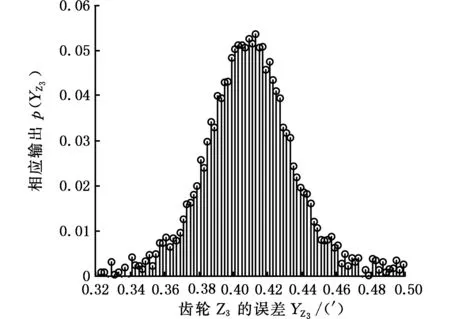
图13 齿轮Z3的误差分布直方图Fig.13 Total error maps of each gear Z3

图14 齿轮Z4的误差分布直方图Fig.14 Total error maps of each gear Z4

图15 齿轮Z5的误差分布直方图Fig.15 Total error maps of each gear Z5

图16 齿轮Z6的误差分布直方图Fig.16 Total error maps of each gear Z6
3.4.2 基于MDCRSA的GTESMG可靠性分析
根据MDCRSA的基本原理,以式(12)和式(13)作为火炮方向机可靠性分析的响应面分析模型。利用蒙特卡罗法对该响应面模型模拟分析10 000次,得到火炮方向机齿轮传动误差的分布特征。模拟过程和分布的直方图见图17,结果表明传动误差Y服从正态分布,均值为9.653′,方差为0.0134′。Y的故障数量是110,失效概率为0.011,可靠度是0.990,满足设计要求。
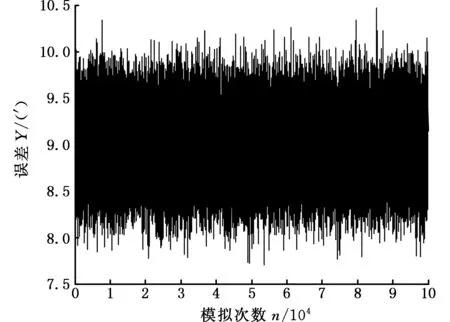
(a)误差Y的一个模拟历史

(b)误差Y的分布图图17 GTESMG可靠性分析输出响应的结果 Fig.17 Output response results of GTESMG reliability analysis
3.4.3 MDCRSA有效性验证
通过与传统方法的对比来验证MDCRSA的有效性和可行性。绝对值法(AVM)和概率法(PM)是火炮方向机可靠度计算的传统方法,经常被用于实际项目的校验与安全性评价。本文用蒙特卡罗法、响应面法以及MDCRSA法进行火炮可靠性分析。在分析过程中,这三种方法在相同的条件下运行。MDCRSA采用7台计算机并行计算,一台计算机计算一个齿轮的相关数据,另一台计算机计算文中提到的其他误差。然后将分析结果作为输入响应对火炮方向机齿轮传动误差进行整体的可靠性分析。三种方法计算所用时间如表6所示。可靠性分析结果如表7所示(忽略40 h以上的系数项)。
由表6可知,MDCRSA响应面函数的拟合时间相当于RSM法拟合时间的4.16%,远短于RSM法和MCM法的拟合时间;从仿真时间比较,MDCRSA算法计算速度是另外两种方法的十万倍至百万倍。表7表明,MDCRSA算法的计算精度相对于另外两种方法也有大幅提高,尤其是对于采样数超过106的模拟,MDCRSA算法可以实现,而RSM法和MCM法几乎是不可能实现的,更不用说其他传统方法。随着模拟次数的增加,上述优势(计算速度和精度)将更加明显。上面的理论分析和案例分析验证了MDCRSA算法的有效性和可行性。
4 结论
本文介绍了MDCRSA算法的基本原理和数学模型,并通过实验验证了该算法的有效性和精确性。计算结果表明,当GTESMG的参考值为10′时,0.990的可靠度基本满足工程要求。MDCRSA不仅能克服传统方法难以解决复杂组件可靠性估算的问题,还极大地节省了计算时间,提高了计算效率。这种算法为GTESMG设计和可靠性分析提供了一种新的研究方法,有助于开发高性能和高可靠性的SMG,值得进一步研究。目前MDCRSA只被用于项目的结果验证,并未在真正的设计过程中使用,如果可以在设计中使用,并最终用来评估设计,将会更进一步验证该算法的有效性。

表6 三种方法可靠性分析的计算时间
表7 GTESMG可靠性分析三种方法的计算结果
Tab.7 GTESMG reliability analysis results by three methods

采样数方法MCMRSMMDCRA1020.97110.95740.99051030.97750.97420.99591040.97960.98510.97881050.98560.99891060.9999
[1] 李蕾. 精密机械设计[M] .北京:化学工业出版社,2005:20-125. LI Lei.Precision Machine Design[M]. Beijing: Chemical Industry Press,2005:20-125.
[2] 李魁武. 现代自行高炮武器系统总体技术[M] .北京:国防工业出版社,2012:40-152. LI Kuiwu. Modern Antiaircraft Weapons System Overall Technical[M]. Beijing: National Defend Industry Press,2012:40-152.
[3] 秦大同,周志刚,杨军,等. 随机风载作用下风力发电机齿轮传动系统动态可靠性分析[J].机械工程学报,2012,48(3):1-8. QIN Datong,ZHOU Zhigang,YANG Jun,et al. Time-dependent Reliability Analysis of Gear Transmission System of Wind Turbine under Stochastic Wind Load [J]. Journal of Mechanical Engineering,2012,48(3):1-8.
[4] SAWALHI N,RANDALL R B. Simulating Gear and Bearing Interactions in the Presence of Faults. Part I: The Combined Gear Bearing Dynamic Model and the Simulation of Localised Bearing Faults[J]. Mechanical Systems and Signal Processing,2008,22:1924-1951.
[5] 李昌,韩兴. 基于响应面法齿轮啮合传动可靠性灵敏度分析[J].航空动力学报,2011,26(3):711-715. LI Chang, HAN Xing. Analysis of Reliability Sensitivity for Gear Engagement Based on Response Surface Methods [J]. Journal of Aerospace Power,2011,26(3):711-715.
[6] LI Qiang, GUO Yunjian, LI Penghui,et al. A Sensitivity Analysis Calculation Method of Gun Barrel Design Parameter Based on Response Surface Method[J]. Journal of Gun Launch& Control, 2010(1):56-59.
[7] SHAN A,WILSON R J,ROTH R N. A New Approach to Statistical Geometry Tolerance Analysis [J]. The International Journal of Advanced Manufacturing Technology,1999,15(3):222-230.
[8] 高卫. 环境温度对齿轮传动机构空程误差的影响[J] .火控雷达技术,1999,28(3):49-52. GAO Wei. Effect of Ambient Temperature on Backlash Error in Gear Drive Mechanism [J]. Fire Control Radar Technology,1999,28(3):49-52.
[9] 林长洪,朱家诚. 齿轮传递误差计算的分析[J] .设计与研究,2011,38(8):10-13. LIN Changhong,ZHU Jiacheng. The Calculation of Transmission Error of Gear [J]. Machinery,2011,38(8):10-13.
[10] 白亚莉,李诚人,王欢欢. 基于综合法的火炮方向机齿轮传动误差分析[J] . 火控雷达技术,2016,45(1):104-108. BAI Yali,LI Chengren,WANG Huanhuan. The Analysis of Gear Transmission Error of Traversing Mechanism of Gun Based on Integrated Method[J]. Fire Control Radar Technology,2016,45(1):104-108.
[11] PUGH C E,BASS B R,Dickson T L. Role of Probabilistic Analysis in Integrity Assessments of Reactor Pressure Vessel Exposed to Pressurized Thermal-shock Conditions[J]. Engineering Failure Analysis,2007,17(3):501-517.
[12] FORSSELL L S.Flight Clearance Analysis Using Global Nonlinear Optimization-based Search Algorithms [C]//Proceedings of the AIAA Guidance, Navigation and Control Conference. Kissimmee,2018:1-8.
[13] BAI Guangchen,FEI Chengwei. Distributed Collaborative Response Surface Method for Mechanical Dynamic Assembly Reliability Design[J]. Chinese Journal of Mechanical Engineering,2013,26(6):1160-1168.
[14] 宋保维,王晓娟. 可靠性设计与分析[M].西安:西北工业大学出版社,2010:62-122. SONG Baowei,WANG Xiaojuan. Reliability Design and Analysis [M]. Xi’an:Northwestern Polytechnical University Press,2010:62-122.
[15] 曾声奎. 可靠性设计与分析[M] .北京:国防工业出版社:2011:112-172. ZENG Shengkui. Reliability Design and Analysis[M]. Beijing: National Defence Industry Press,2011:112-172.
(编辑 袁兴玲)
Reliability Analyses of Gear Transmission Errors of Steering Mechanism of Gun Using MDCRSA
BAI Yali1ZHANG Yi1JI Min2LIU Wenqiang3
1.Department of Mechanical Engineering,Xijing University,Xi’an,710123 2.Department of Mechanical and Electrical Technology,Xijing University,Xi’an,710123 3.Department of Mathematics, Xijing University,Xi’an,710123
To more accurately show the gear transmission errors of the steering mechanism of the gun (GTESMG),reliability analysis of the GTESMG was carried out from a probabilistic perspective by considering multiple factors and dynamic loads. According to GTESMG’s practical applications and theoretical researches,MDCRSA were proposed and the mathematical model of this algorithm was established based on a quadratic function, the detail description of the algorithm was given herein. Then an illustrative real project was used to validate the algorithm in some aspects. The simulation results show that when the design value of GTESMG is as 10′,the reliability is as 0.990,it may meet the requirements of a steering mechanism of gun. Through the comparisons with traditional five analysis methods which were used to evaluate the reliability of gun, the results show that MDCRSA has higher precision and higher efficiency in the reliability analysis of GTESMG. These strengths are likely to become more prominent with increasing simulation times. This research provides an effective and excellent method for the reliability analysis of GTESMG,moreover,the MDCRSA offers a useful insight for designing the reliability of complex gun assemblies.
steering mechanism of the gun;transmission error;reliability;multiple objects multiple factors;multiply distributed collaborative response surface algorithm (MDCRSA)
2016-05-15
2017-04-26
陕西省自然科学基础研究计划资助项目(2013JM8040);陕西省教育厅科研计划资助项目(2013JK1204)
TJ33
10.3969/j.issn.1004-132X.2017.13.013
白亚莉,女,1983年生。西京学院机械工程学院讲师。主要研究方向为机械系统设计与应用。发表论文5篇。E-mail:baileiwdd@163.com。张 毅,男,1969年生。西京学院机械工程学院院长、副教授。冀 敏,女,1975年生。西京学院机电技术系讲师。刘文强,男,1973年生。西京学院数学系讲师。
