基于特征统计量的城市排水泵站设备状态监测算法研究

朱 谨 石春华 王馥莉

（江苏省徐州市水利局 徐州 221000）

基于特征统计量的城市排水泵站设备状态监测算法研究

朱 谨 石春华 王馥莉

（江苏省徐州市水利局 徐州 221000）

围绕城市排水泵站设备健康状态诊断问题，提出了基于特征统计量的设备状态判决方法，通过计算设备运行噪声的MFCC特征参数，计算出其均值和方差两个统计量，形成一维的特征向量，利用短时模糊C均值聚类算法实现测试样本状态的汇聚与判别。由于仅存储特征统计量，大大降低存储样本维数，提高了判决速度，为泵站设备运行状态的在线监测提供了一种有效监测算法。

排水泵站 健康诊断 特征统计量 聚类算法

1 引言

城市排水泵站是城市的基础设施，也是污水处理的最前沿单位。随着城市排水泵站数量不断增加，如何使水泵最大限度发挥功效，延长水泵使用寿命，降低事后的维修保养费用，成为一个迫切需要考虑的问题。

基于支持向量机的泵站设备状态监测方法，可以实现设备运行状态的判决，达到了预期的分类效果。但是支持向量机在分类时是将所有特征参数作为输入向量进行类型判决，运算量较大。尤其是随着机器的运行，模式库存储的特征向量的维数急剧增加，增加了判决时间。本文围绕城市排水泵站设备状态监测问题，研究了城市排水泵站设备运行状态判别方法，研究了基于特征统计量的设备状态判决方法，通过计算的MFCC特征参数，计算出其均值和方差两个统计量，形成一维的特征向量，利用短时模糊C均值聚类算法实现测试样本状态的汇聚与判别。由于仅存储特征统计量，大大降低存储样本维数，提高了判决速度。

2 MFCC系数的样本分布

图1所示为某泵站水泵运行声音测试信号，根据水泵运行状态，将测试信号进行分段处理。整段信号共分割为6小段，其对应类别为：x1—启动，x2—平稳运行（高速），x3—平稳运行（高速），x4—变频调速，x5—平稳运行（低速），x6—停机。其中平稳运行（高速）分为2段，因此属于同一类，可以一段作为样本（训练）序列，一段作为测试序列，验证算法的优劣性。在音频信号以及分割后的6小段时域波形如图1所示。图中，横坐标为时间，单位为s，纵坐标为测量信号幅值。在进行二元模式分类时，可以将x2、x3作为正常状态信号，x1、x4、x5、x6作为故障状态信号。

选取x1与x2作为训练序列，其中x1为故障状态，x2为正常状态，计算其MFCC系数。2.1数据分帧

为了简单起见，每256个数据分一帧，帧移为80，每帧计算一组MFCC数据，共24个，相当于每80个数据计算一组MFCC数据。实际分析时限定分析数据长度为30s，这样约得到16531组MFCC系数。可以每5s给一个判据结果，相应系数为2750组。直接以MFCC系数作为测试样本进行后续判别，由于样本数巨大，运算复杂。

2.2 MFCC系数的样本分布

在大样本下，每一个MFCC系数分布满足正态分布，并且正常与故障两种状态样本分布情况具有明显的异同，因此可以将其统计特性作为特征向量，作为下一步测试的基础。

2.3 计算MFCC系数的矩阵和方差

计算每一个MFCC系数的均值与方差，这样形成24个均值与24个方差，并将均值和方差组成一维的特征向量，其中均值在前，方差在后，正常与故障各组成一个向量。如：

X1=［μ1，…μ24，σ1，…σ24］（故障向量）

X2=［μ'1，…μ'24，σ'1，…σ'24］（正常向量）

图1 某泵站水泵运行声音测试信号及其分段图

这样，模式库中存放的就是两个一维的特征向量（或数组），而不再是16531组MFCC系数（以样本长度30s计算），尤其是模式库更新时，模式库的长度也不再变化，后续计算量将大大降低。

图2 基于模糊聚类的城市排水泵站设备状态监测流程图

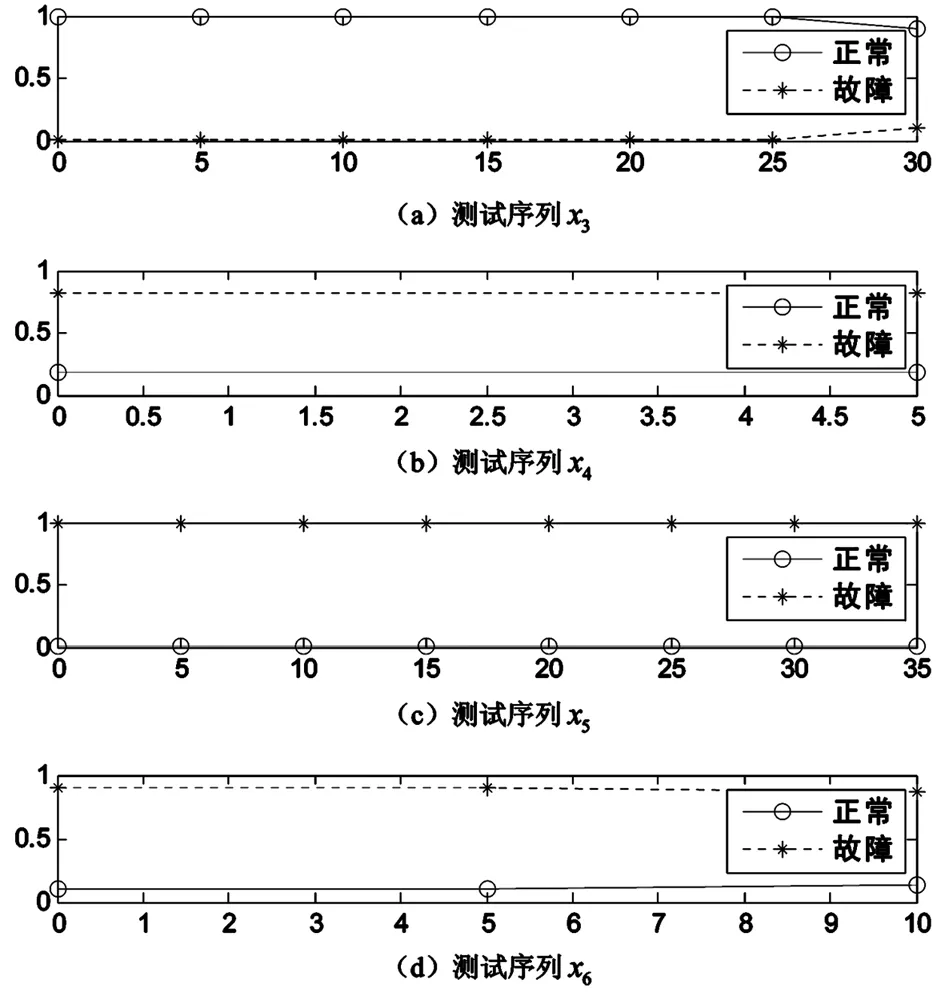
图3 不同测试序列的分类结果图

3 短时模糊C均值聚类算法

短时模糊C均值聚类算法是在模糊C均值聚类算法（FuzzyC-meansAlgorithm，FCMA）上先对测量数据按帧分段，对每一分段信号选取特征参数进行空间映射，然后针对映射后的空间序列应用模糊C均值聚类算法进行模式分类。算法描述如下：

3.1 设备信息流分帧和特征参数空间映射

将测试时间序列按帧分段，对每一段先求MFCC系数，然后计算平均值和标准差，进行特征参数空间映射，形成一个由M个指标来描述的特征向量，即：

为了便于对指标数据进行分析比较，同时避免数据过小指标被淹没，将各指标正则化，即：

这样，便得到正规化矩阵X=（x'ij）N×M。正规化矩阵的每一行被看作分类对象在指标集上的模糊集合，即：

3.2 样本集构建和参数初始化

构建测试样本集 X=｛xl，x2，…xN｝，样本数为 N，聚类数为C（2≤C≤N），迭代次数k=1。现在要将样本集X划分为C类，记为Xl，X2，…XC。选择C个初始聚类中心，记为m1（k），m2（k）…mC（k）。

3.3 计算所有样本与各聚类中心的距离，形成模态束定义目标函数

其中：U=［uji］为模糊分类矩阵；uji∈［0，1］，为样本xj对第i类样本集的隶属度；m∈［0，∞）是加权指数；dji=||xj-mi（k）||为样本xj到第i类样本中心的距离。J（U，V）表示了各个样本到聚类中心的加权距离平方和，权重是样本xj到第i类样本隶属度的m次方。

聚类准则是实现目标函数J（U，V）的最小值。为了求得最佳隶属函数uji，构造拉格朗日函数L（λ，uji）

按最小距离原则将样本xj进行聚类，若d（xj，ml（k）

3.4 更新模态束，重新计算聚类中心mi（k+1）

3.5 若存在i∈｛l，2，…C｝，有mi（k+1）≠mi（k），则k=k+1，进入第（3）步，否则聚类结束。

4 基于模糊聚类的状态分类测试

基于模糊聚类的城市排水泵站设备状态监测流程如图2所示。

实际分析时限定分析数据长度为30s，以5s为单位进行分割，计算出一个特征向量，并与样本库进行对比，并给出一个判据结果。

图3显示了测试序列x3、x4、x5、x6的分类结果。由图可见，每一种测试序列都实现了正确分类。

5 结语

本文提出了一种基于特征统计量的设备状态判决方法。通过计算的MFCC特征参数，计算出其均值和方差两个统计量，形成一维的特征向量，利用短时模糊C均值聚类算法实现测试样本状态的汇聚与判别。由于仅存储特征统计量，大大降低存储样本维数，提高了判决速度■