一个推广的积分中值定理

肖劲森，林全文

（广东石油化工学院数学系，广东茂名525000）

一个推广的积分中值定理

肖劲森，林全文*

（广东石油化工学院数学系，广东茂名525000）

积分中值定理是数学分析的基本定理，它在极限和积分的计算中有着广泛的应用.利用确界定义及介值定理，改进了混合积分中值定理.由该定理，可推导出可积函数具有介值性条件下的积分第一中值定理．

积分第一中值定理；积分第二中值定理；混合积分中值定理

积分第一、二中值定理是数学分析的基本定理，它给出了简化定积分的方法，在求极限、判定某些性质点、估计积分值等方面有着广泛的应用［1-4］.大部分数学分析教材中对两种类型定理表述为两个中值定理.

积分第一中值定理［1］设f（x）在[a，b]上连续，g（x）在[a，b]上可积且不变号，则至少存在一点ζ∈[a，b]，使得：

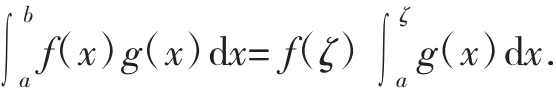
积分第二中值定理［1］设f（x）在[a，b]上单调，g（x）在[a，b]上可积，则存在ζ∈[a，b]，使得：

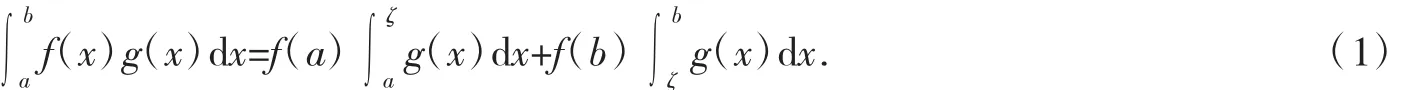
张新元给出了积分第一中值定理条件下类似于第二中值定理的混合积分中值定理［5］．

混合积分中值定理［5］设f（x），g（x）在[a，b]上可积，M，m分别为f（x）在[a，b]的上、下确界，g（x）在[a，b]上不变号，则存在ζ∈[a，b]，使得：

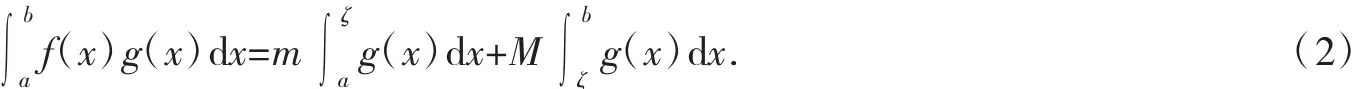
由邓波一文可知，积分第一、二中值定理中函数f（x）和混合积分中值定理中函数g（x）在[a，b]上连续时，点ζ可以在开区间[a，b]中取得［6］．

值得注意的是，积分第二中值定理与混合中值定理在条件为“f（x）在[a，b]上单调，g（x）在[a，b]上可积且不变号”时一致.一个很自然的问题是：积分第一中值定理和第二中值定理之间又有什么关系呢？本文将给出比（2）式更加类似于（1）的表达式.由该表达式，可以推导第一中值定理在函数f（x）在[a，b]上“连续”改为“具有介值性且可积”条件下成立.

定理1设f（x），g（x）在[a，b]上可积，g（x）在[a，b]上不变号，则存在x1,x2∈[a，b]以及至少存在一点ζ∈[a，b]，使得：

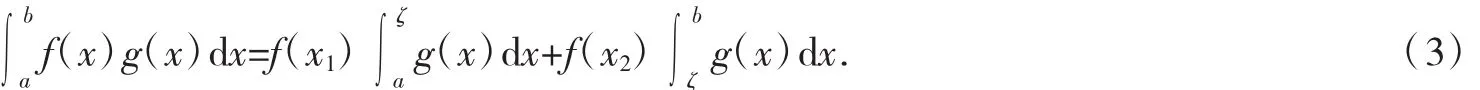
证因为f（x），g（x）在[a，b]上可积，所以f（x）g（x）在[a，b]上可积.不防设g（x）≥0（x∈[a，b]）,M,m分别为f（x）在[a，b]的上下确界，则有：

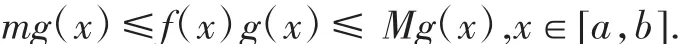
因此由积分的保不等式性可得：

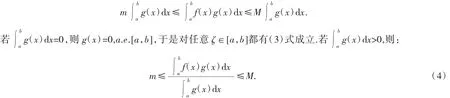
因而存在λ∈（0,1），使得：

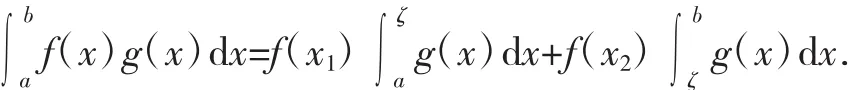
情形2：若（4）式至少一个等号成立，假设：

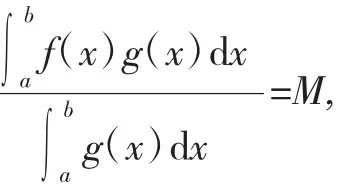
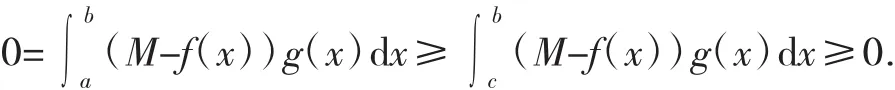
可知f（x）=M a.e.[c，d].因而存在x1,x2∈[c，d]⊂[a，b]使f（x1）=f（x2）=M，及任意ζ∈[a，b]，使得：

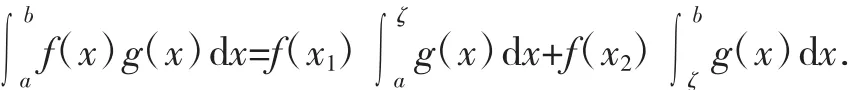
由定理1的证明容易得到，当函数f（x）在[a，b]上单调时，若定理1中f（x）在[a，b]上具有介值性且可积，则由（3）式（或（5）式）容易得到以下当ζ属于开区间（a，b）上的积分第一中值定理．

推论1［7］设函数f（x）在[a，b]上具有介值性且可积，函数g（x）在[a，b]上可积且不变号，则至少存在一点ζ∈[a，b]，使得：

注：由达布（Darboux）导函数介值定理［1］可知，一个闭区间上处处可导函数的导函数与闭区间上的连续函数有着一个共同性质——介值性，因此“具有介值性且可积”条件下的推论1，要比“连续”条件下的结论，以及“具有原函数且可积”条件下的结论更为广泛［8-12］．

［1］刘名生,冯伟贞,韩彦昌.数学分析（一）[M].北京：科学出版社,2009.

［2］华东师范大学数学系.数学分析（上）[M].北京：高等教育出版社,2012.

［3］李泽民.关于积分第二中值定理的改进[J].河南大学学报（自然科学版）,1996，26（1）:14-14.

［4］刘红超.关于积分第二中值定理的研究[D].武汉：湖北大学,2010.

［5］张新元.积分中值定理的较一般情况的几何意义及其推广形式[J].大学数学,2010,26（3）:161-165.

［6］邓波.关于积分第一中值定理的补充说明[J].数学通报,1998（2）:47-47.

［7］李衍禧.积分第一中值定理的推广[J].数学的实践与认识,2007,37（9）:203-206.

［8］关若峰.积分中值定理的推广[J].广州大学学报（自然科学版）,2004,3（6）:499-500.

［9］陈玉.基于微分中值定理的积分中值定理[J].高等数学研究,2013（6）:42-45.

［10］文传军,姚俊.推广的积分第一中值定理的再改进[J].高等数学研究,2011,14（1）:42-44.

［11］刘日成,宋国亮.用介值定理证明积分第二中值定理[J].东北石油大学学报,2008,32（6）:112-114.

［12］李衍禧.关于多重积分中值定理的改进[J].潍坊学院学报,2009,9（2）:75-76.

A Generalized Mean Value Theorem for Integrals

XIAO Jin-sen,LIN Quan-wen*
（Department of Mathematics,Guangdong University of Petrochemical Technology,Maoming 525000, Guangdong,China）

As a fundamental theorem of mathematics analysis,the mean value theorem for integrals is widely applied in calculation of limits and integrals.This paper,by using the definitions of supremum and infimum together with the intermediate value theorem,perfects the mixed mean value theorem for integrals.Based on this theorem,the first mean value theorem for integrable functions with the intermediate value property can be deduced.

First mean value theorem for integrals;Second mean value theorem for integrals;mixed mean value theorem for integrals

O172.2

A

1007-5348（2017）06-0001-03

（责任编辑：邵晓军）

2017-02-02

国家自然科学基金青年基金项目(11501131)；广东省高等学校优秀青年教师培养计划项目（YQ2015117）；茂名市科技局软科学项目（20140340）.

肖劲森(1984-)，男，广东高州人，广东石油化工学院数学系副教授，博士；研究方向：函数论.*通讯作者.