瞬态热线法测量液体导热系数热线尺寸的数值分析

战洪仁, 李世芳, 许洪峰, 王立鹏, 王翠华

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

瞬态热线法测量液体导热系数热线尺寸的数值分析

战洪仁, 李世芳, 许洪峰, 王立鹏, 王翠华

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

利用有限元数值模拟的方法，对瞬态热线法的影响因素：容器壁蓄热和散热、热线长度和半径、容器半径、热线材料以及测量的有效时间进行研究分析.结果表明：热线长度与半径的比值越大，测量精确度越高.根据分析结果对瞬态热线法测量装置进行优化，并将模拟获得的导热系数与标准值进行比较，平均误差为0.011，最大误差为0.023.模拟分析获得的优化模型对测量装置的改进具有借鉴意义.

瞬态热线法； 导热系数； 数值分析； 优化

导热系数作为基础的物性参数，在能源、化工、冶金等学科领域的工程设计及应用研究中发挥着至关重要的作用.目前，各领域科学技术的发展对液体导热系数数据的需求也越来越多，设计出相对精确的液体导热系数测量体系尤为重要.导热系数的测量方法有多种，分为稳态法和瞬态法.瞬态法根据测量原理分为周期热流法和热线法.周期热流法是通过测热扩散率间接计算出导热系数.热线法则根据热源散热量直接得导热系数.在诸多导热系数的研究方法中，瞬态热线法是一种绝对测量方法[1].

近几年人们不断地对热线法测量设备进行研究和改进，取得了很好的成果.如瞬态热针法、瞬态热带法等，测量原理类似，只是测量元件分别为热针和薄金属带，适用于松软颗粒状物质和固体物质导热系数的测量[2-10].在液体导热系数的测量中，由于热线法测量设备简单，测量温度范围宽，测量时间短，辐射及对流对测量结果的影响微小，因此，近些年已逐渐被人们所采用.

本文作者从前人的理论推导和实验结果[11-12]中注意到：应用热线法测量液体导热系数时，试样的尺寸及热线的规格对测量结果有较大的影响.因此，利用有限元方法对其测量过程进行模拟，将不同尺寸、材料的热线在不同容器尺寸下的测量结果进行对比分析，为瞬态热线导热系数测量装置的改进提供了技术指导.

1 瞬态热线法原理

瞬态热线法(transient hot wire)的理想模型是在无限大的均匀液体中插入一长度无限长、直径无限小的金属线作为热源，线热源导热系数无限大，热容量近似为零.初始时刻，二者处于热平衡状态，温度为T0.若用阶跃恒热流对线热源进行加热，单位长度线热源加热功率q为常量，线热源温度升高，继而周围液体产生温升.定义任意时刻距离热线源r处的液体温升为ΔT(r,t)，则过余温度为ΔT(r,t)=T(r,t)-T0.线热源温升速率与周围液体导热能力有关，根据线热源的温升与时间关系得到周围流体的导热系数及热扩散率[11].根据传热控制方程和边界条件得热线表面温升ΔTid(r0,t)与时间对数lnt的直线方程为：

(1)

其中：C为常数，C=eγ=1.781，欧拉常数γ=0.577 2；q为单位长度加热功率；r0为热线半径；t为时间；a为热扩散率；t为热导率.

通过直线的斜率和截距计算得液体的导热系数和热扩散率：

(2)

(3)

其中ΔT′为拟合直线的截距.由公式(2)、(3)可知：在待测液体物性参数不齐全、不能直接计算导热系数和热扩散率的情况下，可以利用瞬态热线法测出待测液体的导热系数和热扩散率.

2 有限元模型

在利用有限单元法(finite element method)进行数值模拟时建立模型的控制微分方程为：

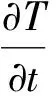
(4)

其中：ρ为液体的密度；c是液体的比热容；r表示半径；Φ代表内热源；t为时间；λ为热导率；T为温度.

根据温度场的对称性，选用实验装置中圆柱腔体轴截面的1/2为研究对象建立二维模型.柱体容器直径10mm，长度70mm；热线直径15

μm，长度50 mm.潘江、王玉刚[13]已验证了网格的无关性.在进行离散化时采用ANSYS进行区域剖分，热线部分采用四边形网格，液体部分采用三角形网格，共划分31 558个单元，如图1所示.

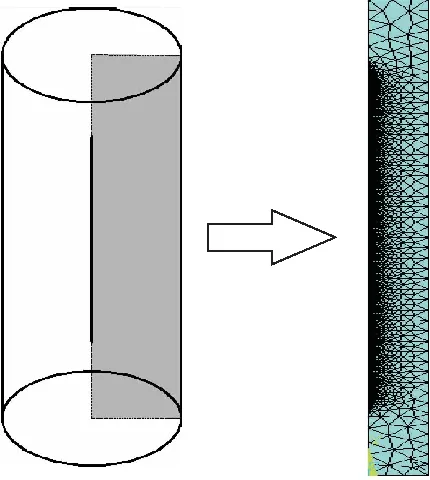
图1 模型及网格划分

计算过程中认为液体静止，不计液体对流与辐射的影响.由于液体为不可压缩流体，选用控制方程(4).设定边界条件时，右边界为t>0时ΔT(r,t)=0，热线与液体连接截面的热流密度q在t>0时为常数.初始时刻整个系统温度为T0，t=0,ΔT(r,t)=0(0≤r<∞).

3 模拟结果分析

热线法理论推导时的假设条件会造成测量结果存在误差，下面就假设条件进行讨论，以期获得最佳的测试结果.数值计算过程选铂丝为热线材料，苯为待测液体，加热功率为0.4 MW·m-1，初始温度为300 K.铂、苯的物性参数见表1.

表1 铂丝、苯物性参数(300 K)

3.1 边界影响

选用直径15 μm、长度50 mm的铂丝热线，以放热和蓄热两种不同的边界进行模拟，得到ΔT随lnt变化曲线，如图2所示，其中ΔT1为容器壁放热曲线，ΔT2为容器蓄热曲线.热线加热时，热量没有传到边界以前，边界是否蓄热对热线温度上升的影响无法呈现.但随着加热时间的继续推移，ΔT与lnt的关系就不再呈线性关系.这是因为由热源放出的热量达到试样表面，试样外部如果是放热条件，温差会增大，如ΔT1曲线；如果试样外部为蓄热条件，则温差变化很慢，如ΔT2曲线.此结果体现了理想模型中液体无限大的假设，说明了在以下模拟过程中采用容器壁散热边界更贴近实际操作.

图2 容器边界蓄热与散热时热线ΔT-lnt图象

3.2 热线尺寸对测量结果的影响

理想的热线长度无限长，直径无限小，但实际中并不可能.为了探究热线尺寸对测量结果的影响，在容器壁散热情况下，模拟了多种热线长度与半径比值不同时的测量过程.容器尺寸不变，取长L为70 mm，半径R为5 mm.先保持热线半径r为7.5 μm，从5 mm至70 mm取不同长度热线进行模拟，结果如图3所示.再保持长度为50 mm不变，从7.5 μm到9.5 μm取不同热线半径进行模拟，结果如图4所示.由图3中温升与时间对数曲线可知：在25 s以内时，不同热线长度模拟结果皆近似重合为直线，但随着加热时间增长，测量曲线已不再呈现直线，且热线越短，直线段也相对越短.由图4可知：相对于热线长度变化的影响，热线半径的变化对结果的影响相对较大.

图3 不同热线长度时ΔT-lnt图

通过大量模拟得出不同热线长度与半径比例的导热系数测量结果，如表2所示，与参考值的比较如图5所示.由图5曲线可知：随着热线长度与半径比例的增大，模拟值越来越接近参考值，即热线长度与半径比例越大，测量结果越精确.热线长径比值较小时误差较大，这是因为热线轴向散热较大.图3中长度较短的两条线有效测量时间较短也说明了这点.所以在选取热线半径时尽量选择目前技术允许的较小半径来提高测量精确度.

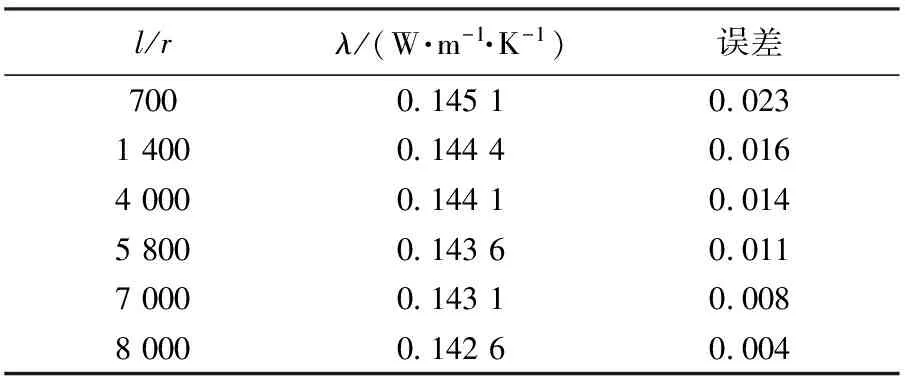
表2 热线长度与半径比例不同时的测量结果

图5 热线长度与半径比例不同时的导热系数值

3.3 容器半径尺寸变化对测量结果的影响

圆柱体容器的长可以根据热线长度决定，但容器的半径尺寸对结果的影响程度如何，目前没有人探究.为分析容器尺寸的影响，现针对不同容器半径进行模拟.容器长度L取70 mm，半径R从5 mm到10 mm间隔取不同尺寸，热线长l为50 mm，r为7.5 μm，热流密度q为0.4 W/m2.模拟结果如图6、表3所示.

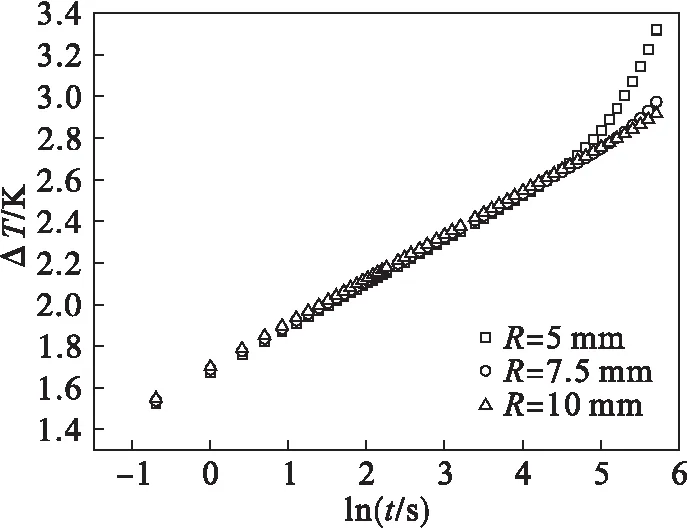
图6 在300 s时不同容器半径下的ΔT-lnt图

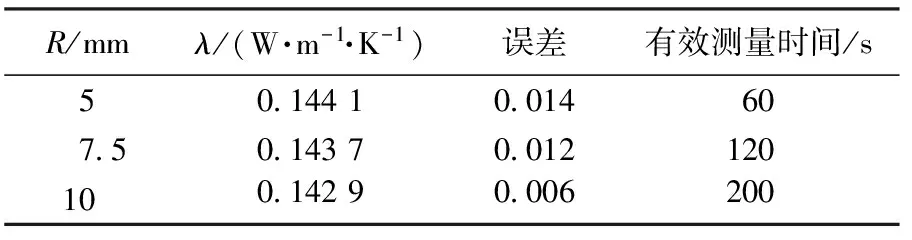
表3 不同容器半径时的有效测量时间及测得苯的导热系数

由图6可知：当测量时间较短，出现拐点以前，容器半径尺寸的变化对导热系数影响较小；随着容器半径的增大，测得ΔT-lnt曲线的直线段延长，说明有效测量时间随容器半径的增大而延长.同时，由表3可以看出：容器的半径相对热线的半径越大，测量的结果越精确.

3.4 热线材料选择与优化分析

由于理想模型和实际情况的差异，自20世纪70年代以来人们的研究重点放在了尽量减少和避免测量误差，一般都选用铂、铑等铂族元素及其合金或钽等稀有金属为热线材料.因为它们具有良好的电学和热学性能，且化学性质稳定.从经济性出发，在常温或温度不高时，我们尝试换用一种经济实惠又普遍易得的热线材料.在所有金属中钨的熔点最高，热容又与铂近似，防腐性能非常好，大多数无机酸对其的侵蚀都很小，化学性质很稳定，不加热时，任何浓度的盐酸、硫酸、硝酸、氢氟酸以及王水对钨都不起作用，当温度升至80～100 ℃时，除氢氟酸外，硫酸、硝酸等对钨发生很微弱作用；常温下，钨与碱溶液不发生反应；具有良好的导电、导热性，因此，选用钨丝做热线.用钨丝做热线，用有限元模型进行分析，分析结果如表4.

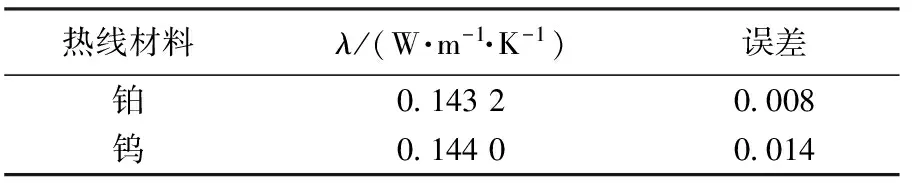
表4 不同热线材料测得的导热系数结果(300 K)

由模拟结果可知：在常温下测量苯等不与钨反应的液体的导热系数时，采用钨丝热线与铂丝的测量结果非常接近，所以，在对待测液体导热系数精确度要求不是太严格的情况下，可以在常温或温度不超过70 ℃时用钨丝作为热线.铂丝价格是钨丝价格的1 000倍左右，选用钨丝不仅精确度高，最重要的是经济实惠，符合现代社会节能减排的要求.

4 结 论

利用有限元法对瞬态热线法测量液体导热系数进行了数值模拟分析，尝试了在容器壁散热情况下进行测量，并通过对不同热线半径、热线长度、容器半径及热线材料的模拟计算，得出以下结果：① 在本文模型中测量的有效时间段为25 s以上.② 在有效测量时间内，容器壁外环境对测量结果的影响可以忽略.③ 热线长度与半径比值越大，测量结果越精确.考虑到加工技术，应使热线半径尽量小.④ 容器半径的尺寸影响有效测量时间的长短，容器半径越大，有效测量时间越长.⑤ 热线长度对有效测量时间也有影响，当热线长度大于30 mm时，对有效测量结果影响较小.⑥ 对某些液体导热系数精度要求不是很严格的情况下，可以在常温或70 ℃以下测量时，用钨丝代替铂丝等作为热线材料，既保证了测量结果又经济实惠.

[1] 刘云飞，吴江涛.瞬态热线法导热系数测量过程的数值模拟[C]//中国工程热物理学会2008年传热传质学学术会议论文集.郑州：中国工程热物理学会，2008.

[2] 刘明.瞬态热线法测量液体导热系数的研究[D].杭州:浙江大学化学工程学院，2010:10-15.

[3] 刘雅珺，李晓静，吴江涛. 二乙二醇单甲醚液相导热系数的实验研究[J].工程热物理学报，2011，32(8):1265-1268.

[4] 陈昭栋.平面热源法瞬态测量材料热物性的研究[J].电子科技大学学报(自然科学版)，2004，33(5):551-554.

[5] 李红梅，朱余良，顾济华.石墨薄膜热导率的研究[J].苏州大学学报(自然科学版)，2010，26(3):48-50.

[6] 邱琳，郑兴华，李谦，等.陶瓷热障涂层的热导率和热扩散率测量[J].功能材料，2010，41(S2):264-267.

[7] GROβ U,SONG Y W,HAHNE E.Measurements of Liquid Thermal Conductivity and Diffusivity by the Transient Hot-strip Method[J].Fluid Phase Equilibria,1992,76:273-282.

[8] HAMMERSCHMIDT U.Thermal Transport Properties of Water and Ice from One Single Experiment[J].International Journal of Thermophysies,2002,23(4):975-996.

[9] DIGUILIO R M.The Thermal Conductivity of Molten Salts and Concentrated Aqueous Salt Solutions[D].Atlanta:Georgia Institute of Technology,1991.

[10]CARSLAW H S,JAEGER J C,FESHBACH H.Conduction of Heat in Solids[J].Physics Today,1962,15(11):74-76.

[11]HEALY J J,DE GROOT J J,KESTIN J.The Theory of the Transient Hot-wire Method for Measuring Thermal Conductivity[J].Physica B+C,1976,82(2):392-408.

[12]RUSCONI R,WILLIAMS W C,BUONGIORNO J，et al.Numerical Analysis of Convective Instabilities in a Transient Short-hot-wire Setup for Measurement of Liquid Thermal Conductivity[J].International Journal of Thermophysics,2007,28(4):1131-1145.

[13]潘江，王玉刚.瞬态热线法导热系数测量的数值模拟[J].中国计量学院学报，2008，19(2):108-113.

Numerical Analysis of Hot Wire Size in Fluids Conductivity Measurement by Transient Hot Wire Method

ZHAN Hong-ren， LI Shi-fang， XU Hong-feng， WANG Li-peng， WANG Cui-hua

(Shenyang University of Chemical Technology, Shenyang 110142， China)

Numerical simulation has been used to investigate the effects of transient hot wire method measuring the conductivity of fluids.The optimization proposal of transient hot wire are proposed after the comparison of numerical data with various condition which include the wall of container in thermal storage and heat dissipation,the length and material of hot wire,the radius of container and effective time of measurement.The ratio of length and radius of the hotline is greater,the higher the accuracy of measurement.According the standard values of conductivity,the average error of simulation is 0.011,the most error is 0.023.The conclusion is of great significant to the reform recommendation of measuring system.

transient hot wire method； conductivity； numerical simulation； optimization

2014-12-08

辽宁省博士科研启动基金项目(20141085)

战洪仁(1964-)，女，山东蓬莱人，教授，博士，主要从事强化传热与节能技术的研究与应用.

2095-2198(2017)02-0162-05

10.3969/j.issn.2095-2198.2017.02.014

O551.3

： A