迎风型紧致算法在二维不可压缩粘性流动中的应用

王华彪，王沧海

（1．重庆电力高等专科学校，重庆400053；2．四川广安发电有限责任公司，四川广安638600）

迎风型紧致算法在二维不可压缩粘性流动中的应用

王华彪1，王沧海2

（1．重庆电力高等专科学校，重庆400053；2．四川广安发电有限责任公司，四川广安638600）

给出一种高精度求解二维不可压缩粘性流动N－S方程的差分算法，该算法对流项具有三阶精度，粘性项具有四阶精度，能精确地求解二维不可压缩粘性流体运动的定常解。同时，用计算机数值计算和图像显示的方法模拟该流体运动压力云与流线图，准确地描述二维不可压缩粘性流动，完成了典型算例。

迎风型紧致算法；纳维－斯托克斯方程；不可压缩粘性流动

纳维－斯托克斯方程（N－S方程）是计算不可压缩流体运动的基本方程，对其数值解法的研究从未间断，紧致差分格式因能取得高精度的近似解引起人们的关注［1］。本文采用改进的迎风型紧致算法求解不可压缩粘性流动的高精度定常解，并用计算机数值计算和图像显示的方法，模拟该运动压力云与流线图［2］，准确地描述二维不可压缩粘性流动。

1 几何模型

不可压缩粘性流体以一定速度流入具有交错双凹槽管道中，如图1所示。在凹槽内会形成漩涡，本文将求解此漩涡运动的最终定常解，并对该运动进行准确描述。

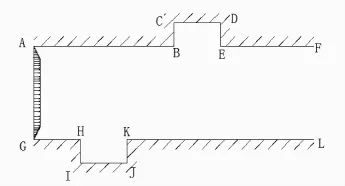
图1 不可压缩粘性流体在交错双凹槽管道中流动问题示意图

本次模拟管道几何尺寸为：AG＝FL＝2，GL＝6，GH＝IJ＝CD＝1，HI＝BC＝0．5，AB＝3。

t＝0时，在计算区域内流体初始参数：

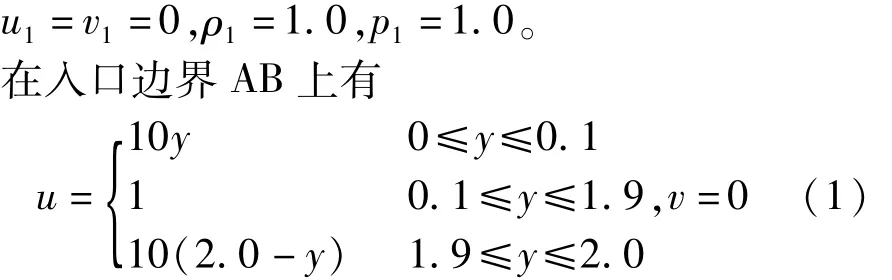
边界条件：①在左边界AB面上为均匀来流，均匀来流参数可由式（1）计算得到；②管道的上下壁面、上凹槽的上壁面、下凹槽的下壁面和凹槽的侧壁面是刚性壁面，速度应满足无滑移反射条件，即在管道的上下壁面、上凹槽的上壁面、下凹槽的下壁面和凹槽的侧壁面上速度为零；③在右边界CD上应满足自由输出条件，即满足

2 计算方法与计算流程图

2．1 数值方法

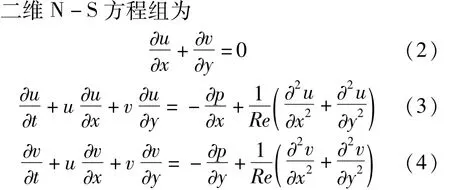
对时间项取简单向前差分格式，压力项取显示中心差分格式，对流项采用迎风型三阶紧致算法差分格式，粘性项采用对称性型四阶紧致算法差分格式，则动量方程式（3）、式（4）的二维迎风型紧致算法差分格式为

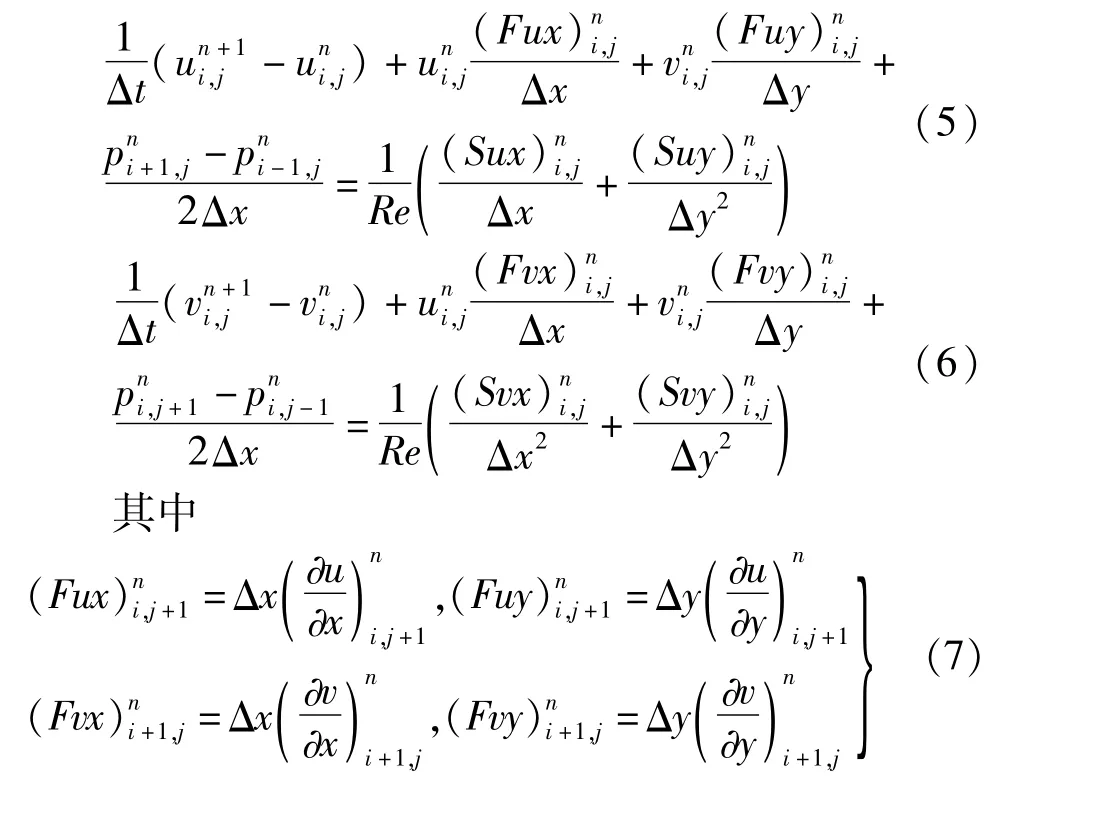
考虑迎风特性后，流项的差分格式为

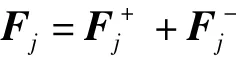
对流项F的三阶迎风型紧致算法差分格式：

当a＞0时，

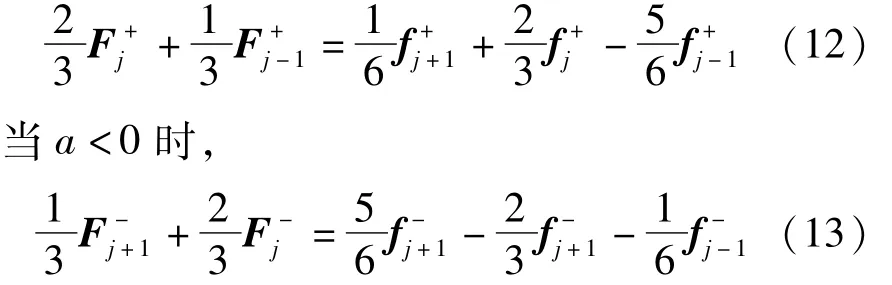
其中，求解Fux＋，Fux－，Fuy＋，Fuy－时，f为u；求解Fvx＋，Fvx－，Fvy＋，Fvy－时，f为v。

粘性项S的四阶紧致算法差分格式为

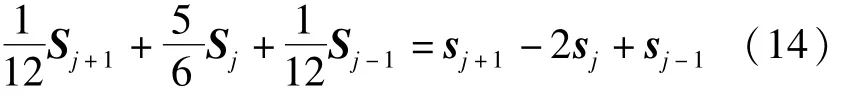
其中，求解Sux，Suy时，s为u；求解Svx，Svy时，s为v。

针对本例是二维不可压缩粘性流动，我们采用人工压缩算法求解。为此，在连续方程中加 p项，将 t连续方程式（2）转化得到

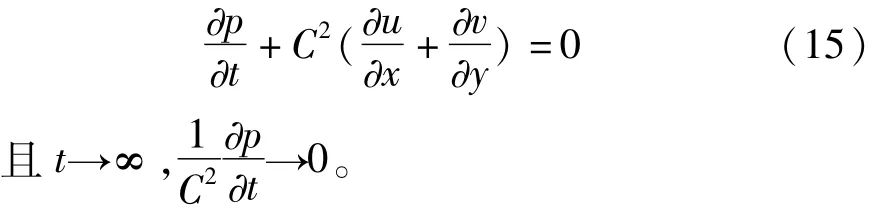
从而得到二维粘性流动N－S方程组人工压缩算法的紧致算法差分格式

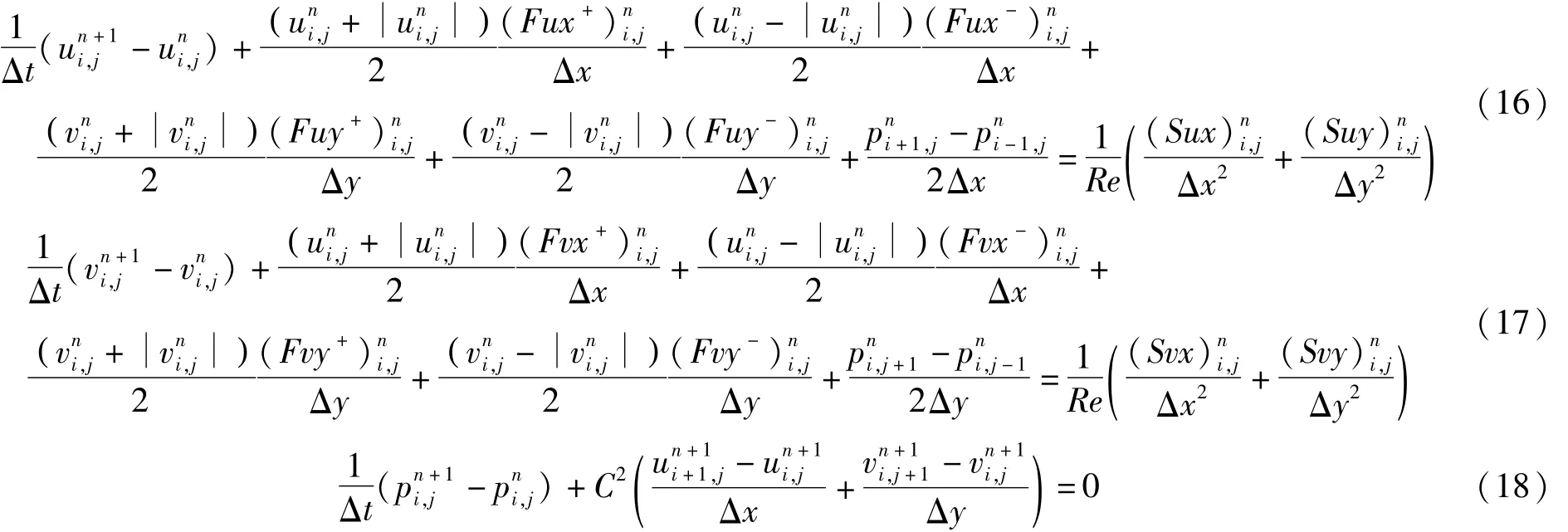
由此，上述方程组的数值解就是本例物理问题的定常解。

2．2 计算网格设计

同一计算区域内，网格数设计越大，流动模拟越细致，但算法也越复杂、计算速度越慢。为了描述流动细节，本例采用的网格数为301×601的交错网格，速度和压力分别设置在整网格点和半网格点上，如图2所示。图中，粗实线表示区域边界，压力p设置在主控单元的中心，速度v在对应压力点的上方，速度u在对应压力点的右侧。

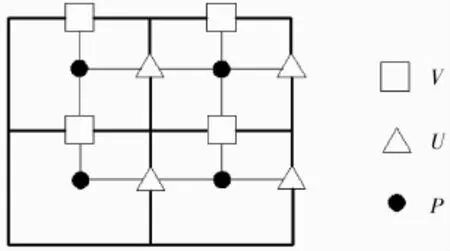
图2 交错网格示意图

3 计算结果及分析

输出数据由tecplot360进行后处理。压力云图见图3，流线图见图4。

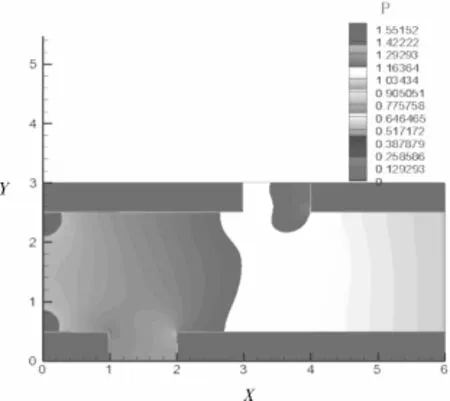
图3 压力云图

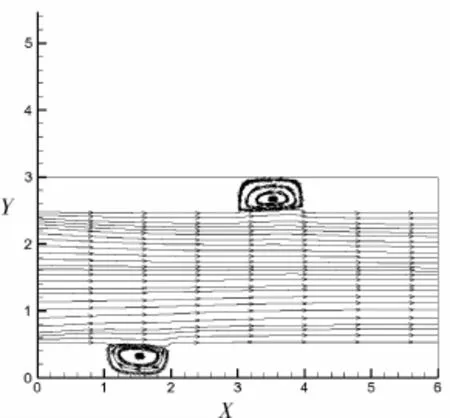
图4 流线图

该计算结果是在Re＝100，网格数为301×601，时间步长为0．001，压缩因子C＝1．8，收敛条件为当计算区域内各点速度的散度绝对值的最大值小于0．000 1时，计算得到的运行步数为347 750步，普通电脑的运行时间大于10 h。如果压缩因子C取1．5，其他条件不变，运行步数约为380 000步，压缩因子取值对收敛性和收敛速度都有较大影响。

4 结论

本文采用迎风紧致算法求解定常不可压缩流体N－S方程，该算法中对流项采用迎风型三阶紧致算法，粘性项采用四阶紧致算法。因此，对流项具有三阶精度，粘性项具有四阶精度，较普通对流算法具有计算精度高、模拟更合理和接近实际流动的优点。压力云图和流线图，算法较为精确且网格数较大，更好地反映了二维不可压缩粘性流动在小尺度范围内的结构，准确地反映了实际运动事实，非常精确地获取了漩涡运动的最终定常解。

［1］ 王婉歆，白乙拉，孙琦，等．一种改进的求解N－S方程的高精度精致算法［J］．渤海大学学报（自然科学版），2012，33（1）：1－5．

［2］ 杨小平，王文豪，马远琼，等．CFD软件在流体力学教学难点中的应用研究［J］．东莞理工学院学报，2016，23（5）：118－122．

A Study on the App lication of the Upw ind Com paction Algorithm in the Two Dimensional Incompressible Viscous Flow

WANG Huabiao1，WANG Canghai2
（1．Chongqing Electric Power College，Chongqing 400053，P．R．China；2．Sichuan Guang an Power Generation Co．，Ltd．of CHD，Guang an Sichuan 638600，P．R．China）

This paper introduces a high accuracy difference algorithm for the solution to the two dimensional incom pressible viscous flow N Sequation，which realizes three order accuracy and four order accuracy for flow and viscos ity items respectively and can be used to reach steady solutions to two dimensional incompressible viscous equations of fluid motion．Meanwhile，numerical computations and image displays can be used to simulate the pressure cloud and the streamlined diagram of the fluid motion，accurately describe the two dimensional incompressible viscous flow，and finish typical examples．

upwind compaction algorithm；N S equation；incompressible viscous flow

O357．1

A

1008 8032（2017）03 0046 03

2017－02－24

王华彪（1989－），助教，研究方向为动力工程。