水库区均质边坡安全可靠度实用分析方法

罗方悦，张 嘎

(清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084)

水库区均质边坡安全可靠度实用分析方法

罗方悦，张 嘎

(清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084)

在水库建设和运行期，库区边坡安全对水库施工和运行影响显著,合理评价水库区边坡的安全性，在保证水库安全和评估环境影响等方面均有重要意义。通过合理简化水库区边坡的强度参数不确定性和水位变化随机性，建立了水库区边坡安全可靠度的实用分析方法。该方法包括2个算法：①通过分析，提出了基于土强度参数二维正态分布的边坡安全系数概率分布算法；②采用Weibull分布描述水位变化规律，提出相关算法,得出了水位变化条件下边坡安全系数的一维先验分布;该方法共有6个参数。采用提出的方法对典型算例进行了计算分析，结果验证了该方法的有效性。该方法对水库区边坡安全评价等方面的研究具有参考意义。

水库区边坡；水位变化；极限平衡方法；可靠度；安全系数

1 研究背景

近年来我国建成运营了一大批高坝水库,这些水库蓄水后导致明显的水位变化，从而显著改变了库区边坡的水文地质环境，对库区边坡安全性造成了不利影响[1-3]。合理评价水位变化条件下库区边坡的安全性，对于保证水库安全、准确评估环境影响有重要意义。已有学者采用数值模拟或者模型试验等方法,对水位变化条件下边坡变形破坏的机理规律和分析方法等方面进行了较深入的研究[3-7]。

边坡的内部结构、材料参数和外部荷载环境均具有明显的不确定性和时变性，是一个不确定性系统。因此,宜采用可靠度来分析边坡的安全性。针对边坡失效及安全可靠度问题，已经发展了多种分析方法，如随机响应面[8-9]、蒙特卡罗[10]、克里金方法[11]、神经网络[12]、随机模糊数学[13]、点估计法[14]、贝叶斯方法[15]等，蒋水华等[16]、张继周等[17]还对计算参数的概率分布进行了探讨。近年来，已有研究利用GIS等方法进行边坡可靠度分析[18]。不过，由于可靠度方法较复杂而不便于应用，实际工程中边坡安全分析仍常采用条分法等规范规定的确定性方法。尽管已有研究对三峡等库区边坡进行了不同角度的安全可靠度分析[19-21]，但针对水库区边坡特点的安全可靠度实用分析方法尚不多见。

在水库的长期运行中，水位变化频繁,且水库区边坡土的强度参数也具有显著的不确定性。而在实际应用中，水库区边坡稳定性分析很少考虑这些特性，其中一个主要原因就是缺乏简便易行、容易理解的安全可靠度实用分析方法。 为此,本文拟将确定性的边坡稳定性分析方法与随机过程理论结合起来，综合发挥安全系数和可靠度理论在边坡稳定性评价中的优点，提出评价水库区边坡安全可靠度的实用分析方法。采用该方法探讨库水位等随机变量对边坡安全的影响规律，为边坡工程风险调控提供依据。

2 基本思路

在水库的长期运行中，其水位显著受到人为调控和自然环境等因素影响，是一个典型的随机变量。在进行边坡安全系数计算时，作为天然材料的边坡土体,其强度参数也具有显著的不确定性。因此，水库区边坡安全可靠度分析主要考虑水位和土体强度参数的随机性，基本思路(图1)如下。

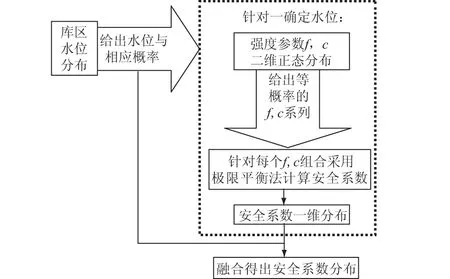
图1 水位变化条件下均质边坡安全可靠度分析思路Fig.1 Flowchart of safety reliability analysis for slopes in the presence of varying water level

(1)边坡土的强度参数一般有2个：摩擦系数f(即tanφ，φ是内摩擦角)和黏聚力c。基于实际工程经验和相关试验资料，采用二维正态分布描述强度参数的概率分布较为合理。选取等概率的强度参数组合系列，用极限平衡法计算确定水位条件下边坡安全系数系列，确定拟合该系列的合理分布类型。

(2) 选取合理的概率分布类型描述库区水位分布。根据上述算法得到系列水位下边坡安全系数一维分布的系列。基于选取的水位概率分布可以确定安全系数系列对应的概率值。对该系列进行融合得到边坡安全系数的先验分布。

需要指出的是，水位变化在边坡中会引起较复杂的非稳定渗流，在有些情况下对边坡稳定性影响较大。本文将边坡的浸润线简化为与水位平齐。这一简化对于水位变化较慢的条件较为适用;对于水位变化较快的情况需要在考虑渗流特性的基础上对浸润线进行修正。不过，对浸润线的简化处理只影响极限平衡法计算得出的安全系数。本文提出的边坡安全可靠度分析方法可以包含考虑更复杂条件的边坡安全系数算法，该简化处理不影响其研究结果。

本文采用的算例为根据实际工程条件简化的一均质边坡，坡度为1∶1.5，高为30 m。边坡土的天然密度为1.8 g/cm3。

3 考虑土强度参数二维正态分布的安全系数算法

3.1 算法描述

由于土强度参数f，c具有高度相关性，已有研究[8-9]认为使用二维正态分布对岩土强度参数进行分布拟合是比较合适的，其概率密度分布函数为

(1)

式中：μf，μc分别为f，c的均值；σf，σc分别为f，c的标准差；r为f，c的相关系数。

基于土的强度试验结果以及工程类比等方式，可以给出土强度参数的可能取值范围。也就是确定了摩擦系数f的下限和上限分别为fa和fb，黏聚力c的下限和上限分别为ca和cb，则有

(2)

这样，在(f,c)平面内就形成确定f，c取值范围的一个矩形区域，区域中心为(μc，μf)，如图2所示。

图2 确定水位下基于土强度参数二维正态分布的边坡安全系数算法原理Fig.2 Principle of algorithm for the safety factor of slopes based on two-dimensional normal distribution of strength parameters of soil at a given water level

在给定水位条件下，对于一组确定的强度参数(f,c)可以采用瑞典条分法算得出边坡稳定性安全系数[22]。基于全概率公式，提出基于强度参数二维正态分布求解边坡安全系数一维分布的算法，从而将二维概率空间降维到一维概率空间上。本文采用计算效率较高的等概率抽样方法计算。在可能取值范围内选择全覆盖且等概率的若干个强度参数组合，计算确定水位下的安全系数，基于这些安全系数得出其一维分布。具体算法如下文所述。

(1) 按照式(3)计算土强度参数可能取值范围的总概率V。

(3)

对于二维正态分布，式(3)难以得出显式函数，因此采用梯形积分公式数值求解。

(2) 在c轴上将可能取值区域[ca,cb]划分成n个条形区间Aj,Aj=[cj,cj+1] (j=1, 2,…,n)(图2)，使得每一条形区间的概率均满足式(4)。

(4)

(3) 针对每一条形区间，再在f轴上将可能取值区域[fa,fb]分成n个小区间Ai，Ai=[fi,fi+1] (i=1, 2,…,n)(图2)，从而在可能取值区域内得到n2个区间Aij，Aij=[fi,fi+1]∩[cj,cj+1] (i=1, 2,…,n;j=1, 2,…,n)。并使得每一方格的概率均满足式(5)。

(5)

(4) 根据上述步骤得到的n2个方格中，每个方格的取值概率是相同的，这就意味着采用该方格的强度参数算得的边坡稳定性安全系数也对应着相等的概率。本文采用每个方格的中心点坐标(fii,cjj)作为该方格对应的强度参数，采用瑞典条分法计算得出给定水位下边坡的安全系数Fs,ij。由于Fs,ij对应的概率是相等的，而且涵盖了所有的可能，因此可以方便地得出安全系数的概率分布，并计算出其一维正态分布的均值和标准差2个参数。

采用式(6)来确定强度参数f,c的取值范围。

(6)

3.2 算例分析及有效性分析

采用上述算法对均质边坡算例进行计算。根据室内试验结果以及工程类比确定该边坡土强度参数二维正态分布参数，如表1所示。

表1 边坡土强度参数的二维正态分布参数

图3 确定水位下边坡安全系数Fs分布的计算结果及正态分布预测结果对比Fig.3 Comparison between calculated results and formulation prediction results of slope safety factor at a given water level

取n=40，对边坡安全系数进行计算。根据1 600个方格计算得出的安全系数及其对应的概率(1/1 600)，按照安全系数从小到大对其对应概率进行累加，就可以方便地得出如图3所示的安全系数概率分布曲线。根据该计算结果可以确定安全系数的均值和标准差分别为：μFs=1.382 0，σFs=0.149 5。

计算概率P(Fs,ij≤Fs|X=x)(i=1,2,…,n;j=1，2，…，n)，可以得到安全系数的分布函数F(Fs|X=x)。为检验该分布偏离对称性的程度，计算该分布的偏度系数α，如式(7)所示。

(7)

式中m3为随机变量Fs,ij的三阶中心矩，其计算式为

(8)

根据计算数据算得偏度系数α为0.148。由于偏度系数越小，分布的正态性越强，因此安全系数计算结果较好地服从一维正态分布。根据μFs=1.382 0，σFs=0.149 5，以式(9)所示的正态分布函数拟合安全系数计算结果，如图3所示。

(9)

从图3中可看出，计算得到的安全系数分布与正态分布的公式预测结果非常接近。图4进一步给出了计算值与公式预测值差值的绝对值e分布。可看出计算值与公式预测值差值很小。图3和图4从不同角度均验证了安全系数服从一维正态分布。

进一步采用单样本Kolmogorov-Smirnov检验。根据图4可得，偏差值D=0.013 4。取显著性水平为0.05，则拒绝正态分布假设临界值D(1 600,0.05)=0.034>0.013 4。所以检验结果表明安全系数服从正态分布。

针对算例探讨了程序离散参数n对计算结果的影响，如图5所示。可以看出，安全系数的均值和标准差在一定程度上受离散参数n的影响，总体上随着n的增大而减小。当n增大到一定值(如30)后，再增大n值对均值和标准差几乎没有影响。这表明本文算法具有稳定的收敛性，当n取值较大时具有较高的计算精度。综合考虑计算量与计算误差，本文取n=40是合适的。

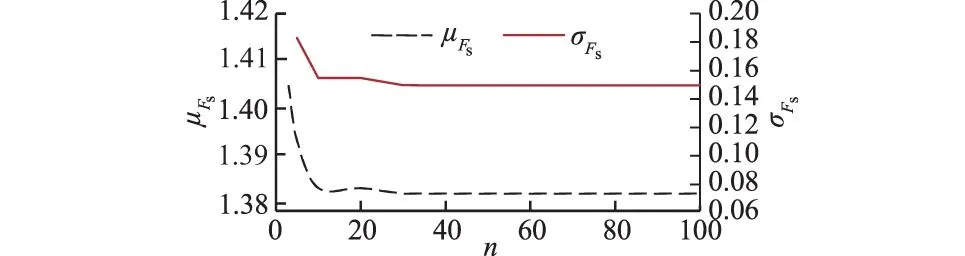
图5 水位20 m时边坡安全系数均值μFs、标准差σFs与离散数量n的关系Fig.5 Relations of average slope safety factor and standard deviation of slope safety factor vs. segment number at water level of 20 m

4 考虑库水位随机性的安全系数算法

4.1 算法描述

已有研究表明，边坡的稳定性安全系数与水位的关系并非单调性关系，需要全面考虑所有可能水位条件下边坡的稳定性。受运行管理控制，库水位在具体时间点上是相对确定的。但是，在水库长期运行过程中，从时间长度来看，库水位受降雨量、发电量、来洪量、泄洪量等多种因素的影响，具有较强的随机分布特性。因此，需要合理确定描述库区水位概率分布类型的函数。从统计学角度看，可以通过分析总结大量水库水位记录资料，研究每日库水位的最大值，将其看作随机变量，以较长时期的一日最大库水位的概率密度分布函数近似单日库水位的概率密度分布函数。以单日最高库水位进行边坡安全性分析可以包络由于库水位变化对边坡稳定造成的影响，这在较长的时间条件下是合理而且必要的。从这一客观情况出发，采用极值分布系列的Weibull分布描述库区水位较为合理。这类分布主要用来分析随机变量在极值情况下的概率特性。Weibull分布一般形式为

(10)

式中:λ,k为水位分布参数;x为水位。

因为受水库运行等条件限制，边坡存在着最低水位hmin和最高水位hmax。根据实际经验，k可以取2，所以要想得到式(10)中的表达式需确定参数λ。应用条件概率公式对库水位的概率密度分布函数进行修正，得到实际可能发生的水位X概率密度分布函数如式(11)所示。

(11)

图6 库区水位概率密度p分布曲线Fig.6 Probability density distribution of reservoir water level

参考实际工程经验和边坡条件，确定本文分析边坡的水位分布参数λ为10，最低水位和最高水位分别为距坡脚0 m和25 m。基于式(10)可得到关于库区水位高度的概率密度分布曲线，如图6所示。

对已确定的一个水位，其发生的概率对应着一个计算得出的的边坡安全系数Fs一维正态分布。因此可对库区水位概率密度分布曲线上所有点对应的安全系数分布进行融合。由全概率公式可知

P(Fs)=∫+∞-∞p(Fs|X=x)pX|hmin≤X≤hmax(x)dx。

(12)

其中，

(13)

4.2 算法应用与有效性分析

图7 计算安全系数对应的概率P直方图Fig.7 Probability histogram of safety factor

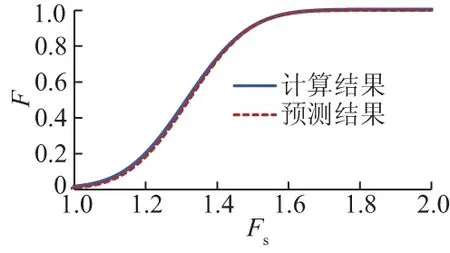
图8 融合后安全系数Fs分布计算结果及正态分布 预测结果对比Fig.8 Comparison between calculated results and formulation prediction results of safety factor after fusion

在库区水位的取值范围内选取m个具有代表性的样本点，采用第2节方法算得m个安全系数Fsm的计算结果。计算概率P(Fs

设边坡安全系数分布为正态分布函数，融合库水位分布后的安全系数Fs分布参数由式(14)计算。

(14)

式中：μFs，σFs分别为融合后安全系数一维正态分布的均值和标准差；μFs,k，σFs,k分别为第k个确定水位xk下基于土强度参数正态二维分布计算得到的边坡安全系数一维正态分布的均值和标准差；wk为要融合的安全系数一维正态分布的概率值，即水位xk对应的概率值。

图9 融合后边坡安全系数 Fs分布计算值与公式预测值 偏差的绝对值e关系曲线Fig.9 Absolute deviations between calculated results and formulation prediction after fusion

根据式(14)计算得：μFs=1.323 9，σFs=0.134 3。根据上述均值和标准差得出的正态分布的公式预测结果如图8虚线所示，可知其与计算得到的融合后安全系数分布非常接近。图9进一步给出计算值与公式预测值差值的绝对值分布。可知计算值与公式预测值差值很小。图8和图9均验证安全系数服从一维正态分布，假设成立。

进一步采用单样本Kolmogorov-Smirnov检验。由图8可得，误差值D=0.024 6。取显著性水平为0.05，则拒绝正态分布假设临界值D(283, 0.05)=0.080 8>0.024 6。所以检验结果表明安全系数服从正态分布。

5 结 论

本文合理简化水库区边坡的强度参数离散性和水位变化随机性的特性，建立了水库区边坡稳定性安全可靠度的分析方法。该方法主要包括如下2种算法：

(1) 对于确定的水位，提出了基于土强度参数二维正态分布的边坡安全系数算法,得出边坡安全系数一维概率分布，实现了二维概率空间到一维概率空间的降维。

(2) 采用Weibull分布描述水位变化过程。提出了相关算法，得出水位变化条件下边坡安全系数的一维先验分布，实现了2个独立随机变量的一维概率分布的融合，并验证了算法的有效性。

本文方法共6个参数，包括1个水位分布参数λ，以及5个土强度分布参数μf，μc，σf，σc，r。其中，水位分布参数可以根据水位观测等资料确定，强度分布参数可以根据土的力学特性试验结果以及工程经验等综合确定。

[1] 中村浩之，王恭先. 论水库滑坡[J]. 水土保持通报，1990，10(1)：53-64.

[2] 廖红建，盛 谦，高石夯，等. 库水位下降对滑坡体稳定性的影响[J]. 岩石力学与工程学报，2005，24(19)：3454-3458.

[3] 陈勋辉，黄耀英，李春光，等. 地下水位对雾江滑坡体稳定性的影响[J]. 长江科学院院报, 2017, 34(1): 104-108.

[4] 汪 斌，唐辉明，朱杰兵，等. 考虑流固耦合作用的库岸滑坡变形失稳机制[J]. 岩石力学与工程学报，2007，26(增2)：4484-4489.

[5] 唐志政, 汪 洋, 吴 晔. 库水位波动条件下万州瓦窑坪滑坡稳定性分析[J]. 水文地质工程地质, 2015, 42(1): 129-133.

[6] 唐晓松, 郑颖人, 唐辉明, 等. 水库滑坡变形特征和预测预报的数值研究[J]. 岩土工程学报, 2013, 35(5): 940-947.

[7] 杨春宝, 朱 斌, 孔令刚, 等. 水位变化诱发粉土边坡失稳离心模型试验[J]. 岩土工程学报, 2013, 35(7): 1261-1271.

[8]SHAMEKHI E, TANNANT D D. Probabilistic Assessment of Rock Slope Stability Using Response Surfaces Determined from Finite Element Models of Geometric Realizations[J]. Computers and Geotechnics, 2015, 69: 70-81.

[9] 蒋水华, 祁小辉, 曹子君, 等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学, 2015, 36(3): 809-818.

[10]桂 勇, 邓通发, 罗嗣海, 等. 基于蒙特卡罗边坡稳定二元体系的建立与应用[J]. 岩土力学, 2014, 35(7): 1979-1986.[11]罗正东, 董 辉, 陈 铖, 等. 基于克里金模型的边坡稳定可靠度分析方法[J]. 岩土力学, 2015, 36(增1): 439-444.[12]舒苏荀, 龚文惠. 二维随机场下边坡稳定性的径向基函数神经网络分析法[J]. 岩土力学, 2015, 36(4): 1205-1210.

[13]WU Yi-ping, CHENG Cong, HE Gao-feng,etal. Landslide Stability Analysis Based on Random-fuzzy Reliability: Taking Liangshuijing Landslide as a Case[J]. Stochastic Environmental Research and Risk Assessment, 2014, 28(7): 1723-1732.

[14]TSAI Tung-lin, TSAI Ping-yu, YANG Pei-jhang. Probabilistic Modeling of Rainfall-induced Shallow Landslide Using a Point-estimate Method[J]. Environmental Earth Sciences, 2015, 73(8): 4109-4117.

[15]SHU Qing-lian, YANG Ling-qiang, ZANG Pan-ying. Application of Bayesian Method in Stochastic Analysis of Rock Slope Stability[J]. Applied Mechanics and Materials，2011，94/96: 516-519.

[16]蒋水华，魏博文，李 聪. 考虑锚索腐蚀性能退化的边坡可靠度分析[J]. 长江科学院院报, 2017, 34(3): 90-95.

[17]张继周，缪林昌. 岩土参数概率分布类型及其选择标准[J]. 岩石力学与工程学报, 2009, 28(增2): 3526-3532.

[19]BI Ren-neng, EHRET D, XIANG Wei,etal. Landslide Reliability Analysis Based on Transfer Coefficient Method: a Case Study from Three Gorges Reservoir[J]. Journal of Earth Science, 2012,23(2): 187-198.

[20]彭 令, 牛瑞卿, 陈丽霞. GIS支持下三峡库区秭归县滑坡灾害空间预测[J]. 地理研究, 2010, 29(10): 1889-1898.

[21]谭晓慧, 余 兵, 王茂松, 等. 水库边坡稳定的可靠度分析[J]. 岩土力学, 2008, 29(12): 3427-3430.

[22]FELLENIUS W. Erdstatisch Berechnungen (Revised Edition)[M]. Berlin: W. Ernst und Sohn，1939.

(编辑：黄 玲)

Simplified Analysis of Safety Reliability of Homogeneous Slopesin Reservoir Area

LUO Fang-yue, ZHANG Ga

(State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China)

The safety of slopes near reservoir has significant impact on the construction and operation of reservoir. Reasonable assessment of slope safety is of vital importance in assuring the safety of reservoirs and evaluating environmental effect. A new simplified method was proposed to analyze the safety reliability of slopes near the reservoir on the basis of reasonable simplification of the uncertainties in the soil strength parameters and the randomness of water level change. An algorithm was proposed to obtain the probability distribution of safety factor according to the two-dimensional normal distribution of soil strength parameters at a given water level. The Weibull distribution was used to describe the stochastic characteristic of water level. The probability distribution of safety factor could be computed using the proposed algorithm. Six parameters were required for the method. The method was used to analyze typical slope case and its effectiveness was preliminarily confirmed. The method provides references for the safety evaluation of slope in reservoir area.

slope in reservoir area; change of water level; limit equilibrium method; reliability; safety factor

2016-04-27；

2016-06-13

国家自然科学基金项目(51479096)

罗方悦(1995-)，女，云南西双版纳人，主要从事边坡稳定性的研究工作，(电话)010-62797085(电子信箱)luofy14@mails.tsinghua.edu.cn。

张 嘎(1976-)，男，山东淄博人，教授，博士，主要从事岩土工程方面的教学与科研工作，(电话)010-62795679(电子信箱)zhangga@tsinghua.edu.cn。

10.11988/ckyyb.20160410

2017,34(7):106-110,115

P642

A

1001-5485(2017)07-0106-05