一种基于SVM的负载识别算法
2017-07-19张冬松
张冬松,马 琪
(杭州电子科技大学 微电子CAD研究所,浙江 杭州 310018)
一种基于SVM的负载识别算法
张冬松,马 琪
(杭州电子科技大学 微电子CAD研究所,浙江 杭州 310018)
负载识别技术能够自动识别出电网中正在使用的负载类型。文中提出一种基于支持向量机SVM的负载类型识别算法,由于SVM只支持二分类,算法采用了One-Against-One组合多个SVM的方法来构建多分类器进行负载识别。通过提取特征量并进行归一化预处理构建训练集来训练SVM多分类器,运用遗传算法对SVM参数进行寻优,寻找识别准确率最高的参数组合。测试结果表明,该SVM多分类器的识别效果较好。
支持向量机;遗传算法;负载识别
负载监测技术如智能仪表可以为发电厂提供实时的能源消耗、最大需求、消耗模式和电能质量,电力公司可利用这些信息进行分析,提供一些激励项目来鼓励用户使用能效更高的设备,以及帮助电力公司有效管理电力需求并建立未来的扩张计划。负载监测技术中的识别电网中正在使用的负载类型,能够帮助人们监测管理电网中正在使用的负载,提高能源利用效率[1]。还可应用于监管电网违禁电器。
文献[2~8]是基于负载稳定状态下的一些特征如有功功率、无功功率、电流谐波等进行负载识别的。文献[9]采用两阶段的模糊分类方法,第一阶段采用基于Fuzzy c-Means聚类方法来初步确定参数和模糊的If-Then规则,第二阶段采用EBPA算法(Error Back-Propagation Algorithm)和遗传算法(GA)来寻找好的参数来提高负载识别的准确率。文献[10]通过ESD(Edge Symbol Detector)来检测负载的接通断开事件,并通过3个特征基于支持向量机进行负载识别。文献[11]提出使用隐马尔可夫模型(Hidden Markov Model, HMM)和稀疏的维特比算法(Sparse Viterbi Algorithm)来进行负载识别。
实验所用的电流数据是通过Stm32单片机采集的,即将传感器接入负载所在支路,用Stm32单片机的A/D模块采集传感器信号。从负载的电流波形中提取了一些特征量,根据这些特征,采用基于支持向量机(Support Vector Machine,SVM)的多分类器对负载类型进行识别。由于不同的参数会直接影响SVM分类性能,基于遗传算法对SVM参数进行寻优。
1 电流特征量及数据预处理
在负载识别领域广泛使用的一些特征有:过零率、电流峰值、电流绝对值均值、电流均方根值、电流方差、总谐波失真THD(Total Harmonic Distortion)、波峰因数(Crest Factors)、波形因素(Form Factors)。
单个周期电流过零的次数就是过零率,也就是单个周期采样电流由正变负以及由负变正的次数。总谐波失真THD计算公式如下,式中Ih为电流第h次谐波成分
(1)
波峰因素是电流的峰值与电流的均方根值的比值;波形因素是电流的均方根值与电流基波分量的比值;除了那些广泛使用的特征外,根据对各负载电流波形数据的分析,提取了3次、5次、7次、9次谐波在除基波以外的谐波成分中所占比例及电流波形斜率方差,3次谐波比例计算公式为
(2)
同理可得5次、7次、9次谐波在除基波以外的谐波成分中的比例。电流波形某点斜率近似认为是相邻两个采样点直线斜率,计算公式如式(3)所示,电流波形斜率方差计算公式如式(4)所示
(3)
(4)
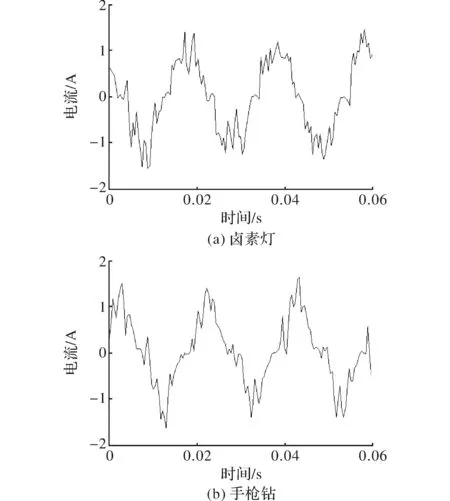
图1 卤素灯和手枪钻的电流波形图
电流波形斜率方差能够有效区分一些在其他特征很相似的负载,卤素灯和手枪钻的电流波形如图1所示,随机选取500个样本的卤素灯和手枪钻的电流波形斜率方差对比如图2所示。
基于SVM对负载进行识别,为减小数据间的差异过大对SVM分类识别的影响,需要对提取的特征量进行归一化预处理,方法如下
xk=(xk-xmean)/xvar
(5)
其中,xmean为某一维特征量序列的均值;xvar为对应维特征量的方差,对提取的12维负载特征数据都按式(5)处理。
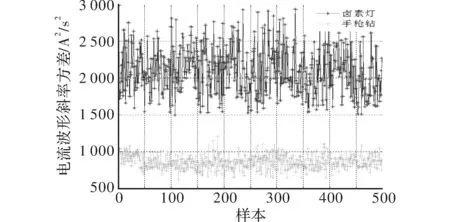
图2 卤素灯和手枪钻的电流波形斜率方差对比图
2 支持向量机SVM原理
支持向量机SVM最早于1995年由Cortes & Vapnik提出[12],是针对二分类的一种算法,其基本思想是寻找一个超平面,使得两类数据距离这个超平面的间隔最大化。当两类数据是线性可分的时候,其分类函数为
f(x)=ωTx+b
(6)
其中,f(x)>0对应一类数据点;f(x)<0对应另一类数据点。用于负载识别的特征量显然是非线性数据集,需要引入核函数来将特征量映射到高维空间来解决非线性的问题[13],但无限增加维数会引发维数灾难,同时也会使得模型的泛化能力变差,因此引入松弛变量ξ={ξ1,ξ2,…,ξn},允许对待分类的样本有一定程度的错分。通过增加惩罚值和松弛变量,问题将转化为解决以下优化问题
subject toyi(ωTφ(xi)+b)≥1-ξi
ξi≥0,i=1,…,n
(7)
式中,φ(xi)将xi映射到一个高维空间;C是一个>0的参数。由于向量ω可能是维数很高的高维向量,通常转化为求解下面的对偶问题
subjecttoyTα=0
0≤αi≤C,i=1,…,n
(8)
其中,e=[1,…,1]T是一个元素全为1的向量,Q是一个n行n列的矩阵,Qij=yiyjK(xi,xj),K(xi,xj)=φ(xi)φ(yj) 为核函数。当式(8)解决以后,根据原来的对偶关系,最优的ω满足

(9)
决策函数

(10)
其中,x为待分类的测试向量;xi为支持向量;αi为权重系数;b为一个常数。SVM可以通过一个训练数据集将不同类别之间的差异最大化,它作为一个广泛使用的分类器可以有效区分不同负载特征之间的差别,达到负载识别的目的。
3 SVM多分类器设计
SVM是一个二类分类算法,而负载种类繁多,因此需要一个能够分类多类的算法,可以通过采用基于One-Against-One的方法来组合多个SVM进行负载识别。该方法首先对任意两类负载之间均设计一个SVM二分类器,当要对k个类别负载进行识别(多分类)时就需要有k(k-1)/2个SVM。当对一组未知负载类别的特征量进行识别(多分类)时,对每个SVM二分类器的结果进行投票,最后得票最多的负载类别即为该组未知特征量的负载类别。例如,如果需要识别A、B、C3类负载,分别对(A,B)、(A,C)和(B,C)设计一个SVM二分类器。对于一组待识别负载类别的特征量,投票形式如下:
(A,B)-SVM Classifier,如果是Awin,则A=A+1;否则B=B+1;
(A,C)- SVM Classifier,如果是Awin,则A=A+1;否则C=C+1;
(B,C)- SVM Classifier,如果是Bwin,则B=B+1;否则C=C+1;
最终识别(多分类)结果为max(A,B,C)。
4 基于SVM多分类的负载分类器训练
首先从原始负载电流数据提取出相应的特征量,构成负载识别的原始特征数据集,对这个特征数据集进行归一化得到用于负载识别的特征数据集。将这个特征数据集的25%作为基于SVM多分类的负载分类器的训练集,来训练各个SVM二分类器。
SVM分类器需要先确定惩罚参数c和核参数gamma(g),gamma是径向核函数[14]作为kernel后,函数自带的一个参数为了提高SVM分类器的分类准确率,采用遗传算法(GA)结合K折交叉验证寻找较好的参数c和g组合。K折交叉验证即将训练集分为K个子集,分别让每个子集作为测试集,其余作为训练集来训练SVM,这样会得到K个模型,用这K个模型测试集分类准确率的平均值来评估参数c和g的优劣,K折交叉验证可以有效地避免过学习以及欠学习状态的发生,一般K≥2,只有在原始数据集合数据量小时才尝试取2,实验采用K=5。
整个负载分类器的训练过程如图3所示,GA对SVM的参数寻优即训练都是离线做的,用寻优后的参数训练出来的SVM才是真正用于负载识别的。
5 基于遗传算法的参数寻优
遗传算法(Genetic Algorithm,GA)是一种全局优化的随机搜索算法,算法包含选择、交叉和变异3个操作。遗传算法是从代表问题可能潜在解集的一个种群开始,按照适者生存和优胜劣汰的原理,逐代演化产生越来越好的近似解[15]。遗传算法第一步是对染色体进行编码,实验采用LIBSVM在Matlab R2014a平台进行,LIBSVM是台湾大学林智仁教授等开发设计的一个SVM软件包[16]。需要对惩罚参数c和核参数g进行寻优,因此一条染色体代表一对c和g组合。对染色体采用二进制编码,染色体总长度为24位,每12位表示一个参数,其中前8位表示整数部分,后4位表示小数部分,随机产生20个染色体序列作为初始种群。

图3 负载分类器训练过程
在进化过程中,依据个体适应度值来决定保存还是丢弃,适应度值采用一条染色体对应的c和g参数组合的交叉验证准确率。当有两条染色体的交叉验证准确率相同时,选择c较小的c和g组合作为更好的参数,因为过高的c会导致过学习状态的发生,即训练集分类准确率很高而测试集分类准确率很低(分类器的泛化能力降低),所以在相同的交叉验证准确率下选择较小的c的染色体。重复进行选择交叉变异操作,直到达到最大进化代数或最佳个体在一定代数内不发生变化。
6 实验结果及分析
采用LIBSVM进行负载分类器的训练和测试,实验采用了电磁炉、空调、日光灯等10种负载,训练集的样本总数为9 856个,测试集样本总数为30 583个,SVM采用径向基(RBF)核函数。采用GA寻找较优参数的适应度进化曲线如图4所示,采用决策树,BP网络以及对参数c和g采用默认参数以及用遗传算法寻优后的参数的负载识别(分类)准确率结果对比如表1所示,同默认参数相比,测试集遗传参数寻优后的负载识别整体准确率达到了98.3%,提升了1.4%以上。对于负载识别,提出的方法比决策树和BP神经网络的识别准确率要高。

表1 采用决策树,BP网络及SVM的负载识别(分类)准确率结果对比
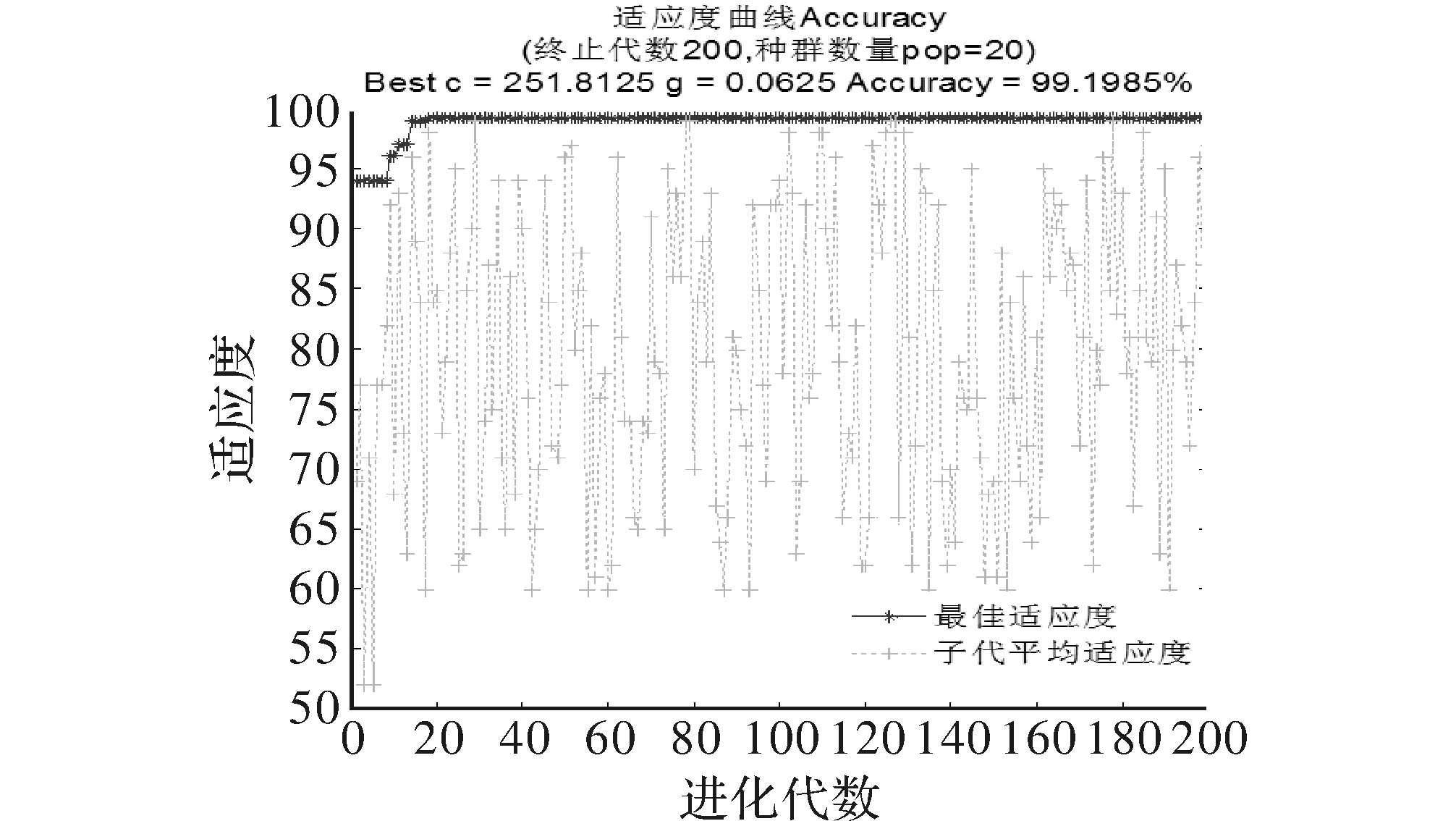
图4 利用GA寻优的适应度(准确率)曲线
采用遗传参数寻优后参数的负载分类器进行负载识别,得到各个负载识别的具体结果如表2所示,其中电磁炉有4个工作状态(功率分别为1 200 W、1 400 W、1 800 W和2 100 W),调光灯采用了4个工作状态,(分别为60°、75°、90°和120°)。空气压缩机的识别准确率最低,但也超过了94%,实验结果表明,基于SVM的多分类方法能够较为准确的识别出负载类型。

表2 基于SVM的负载识别实验结果
[1] Anonymous.BP statistical review of world energy[R].Houston:BP Global,2016.
[2] Umeh K C,A Mohamed.A rule-based expert system for harmonic load recognition[C].Kuala Lumpur:Power and Energy Conference,2004.
[3] Drenker S,Kader A.Nonintrusive monitoring of electric loads[J].IEEE Computer Applications in Power,1999,12(4):47-51.
[4] Mahmood Akbar,Zubair Ahmad Khan.Modified nonintrusive appliance load monitoring for nonlinear devices[C].Pakistan:Multitopic Conference,INMIC 2007,IEEE International,2007.
[5] Laughman C.Advanced nonintrusive monitoring of electric loads[J].IEEE Power and Energy Magazine,2003(6):56-63.
[6] Cole A,Albicki A.Nonintrusive identification of electrical loads in a three-phase environment based on harmonic content[J].IEEE Power and Energy Magazine,2000(1):24-29.
[7] Jie Mei,Dawei He,Ronald G,et al.Random forest based adaptive non-intrusive load identification[C].Beijing:International Joint Conference on Neural Networks(IJCNN), 2014.
[8] Lin Y H,Tsai M S.A novel feature extraction method for the development of nonintrusive load monitoring system based on BP-ANN[C].Tainan:International Symposium on Computer, Communication,Control and Automation (3CA),2010.
[9] Lin Y H, Tsai M S, Chen C S. Applications of fuzzy classification with fuzzy c-means clustering and optimization strategies for load identification in NILM systems[C]. Nanjing:IEEE International Conference on Fuzzy Systems, 2011.
[10] Jiang L, Luo S, Li J. Automatic power load event detection and appliance classification based on power harmonic features in nonintrusive appliance load monitoring[C].Shanghai:Industrial Electronics and Applications,IEEE, 2013.
[11] Makonin S, Popowich F, Baji I V, et al. Exploiting HMM sparsity to perform online real-time nonintrusive load monitoring[J].IEEE Transactions on Smart Grid, 2016, 7(6):1-11.
[12] Vapnik V N.Statistical learning theory[M].New York:Wiley,1998.
[13] Jiang L,Li J,Luo S,et al.Literature review of power disaggregation[C].Shanghai:IEEE International Conference on Modelling Identification and Control,2011.
[14] 张子瑜,陈进,史习智,等.径向高斯核函数时频分布及在故障诊断中的应用[J].振动工程学报,2001,14(1):53-59.
[15] 韩盈盈,章毅鹏,沈鸿平,等.基于遗传算法和0-1规划的规则图形碎片拼接[J].电子科技,2015,28(5):136-139.
[16] Chang C C, Lin C J. LIBSVM: A library for support vector machines[J].ACM Transactions on Intelligent Systems & Technology,2011(2):1-27.
A Load Identification Algorithm Based on SVM
ZHANG Dongsong,MA Qi
(Microelectronics CAD Center,Hangzhou Dianzi University,Hangzhou 310018,China)
Load identification technique can identify the different types of loads in a power system. This paper presents a load identification algorithm based on support vector machine (SVM), which adopted the one-against-one method which combined multiple SVMs to build a multi-classifier to deal with load identification because SVM is only a binary-classifier. In this paper, the SVM-based multi-classifier was trained by extracted characteristic quantities normalized, during which the genetic algorithm (GA) was used to optimize the SVM parameters for the highest recognition accuracy. The experimental results show the validity of the SVM-based multi-classifier.
support vector machine;genetic algorithm;load identification
2016- 11- 01
张冬松(1991-),男,硕士研究生。研究方向:嵌入式系统设计。马琪(1968-),男,博士,研究员。研究方向:嵌入式系统设计。
10.16180/j.cnki.issn1007-7820.2017.08.016
TP391.4
A
1007-7820(2017)08-059-04
