基于4WS车辆的转向稳定性控制算法研究

龚戌伟, 孙 涛

(上海理工大学 机械工程学院，上海 200093)



基于4WS车辆的转向稳定性控制算法研究

龚戌伟, 孙 涛

(上海理工大学 机械工程学院，上海 200093)

在四轮转向(4WS)车辆的基础上，结合车辆的横摆角速度和质心侧偏角，通过改变车轮的转向角来提高车辆的稳定性和操纵性。建立参考模型，七自由度车辆模型，线性二次最优控制模型和PID控制模型，结合驾驶员模型和道路模型，在Matlab/Simulink软件中进行系统建模仿真。仿真结果显示，设计的4WS车辆的转向稳定性控制系统算法具有一定的有效性。

横摆角速度；质心侧偏角； Matlab/Simulink；线性二次最优控制；PID；系统建模

四轮转向(4WS)系统是在传统车辆的基础上，即在后轮之间增加转向系统，目前4WS车辆的机械结构设计已相对完善，而如何通过设计控制算法在提高4WS车辆稳定性上有更大发展空间。众多学者在4WS的控制算法上进行了研究。文献[1]应用μ综合鲁棒控制理论，针对横摆角速度与侧倾角速度对车辆进行逻辑控制提高车辆的防侧倾能力，加强车辆的稳定性；文献[2]在建立线性二自由度的基础上，采用最优控制理论，对DYC作为控制目标来提高车辆的稳定性；文献[3]根据四轮转向车辆的转向特性，利用建立的转向模型，以轮胎作为研究对象，结合车辆的侧向动力学来研究提高车辆稳定性的算法。

本文在四轮转向车辆(4WS)的基础上，通过结合车辆的纵向动力学和侧向动力学性能，建立二自由度车辆模型作为参考模型，建立七自由度模型来模拟真实车辆。通过观测车辆的横摆角速度及质心侧偏角，求出理论值与实际值的偏差量。采用线性二次最优控制算法以及PID控制的方法，调控车辆4个轮胎的转向角来减小上述偏差量，提高车辆稳定性。利用Matlab/Simulink进行模拟仿真，使车辆在预测的道路模型中行驶轨迹偏差达到最小。

1 车辆模型

1.1 二自由度车辆模型

本文需要建立一个模型作为参考标准。假设忽略左右轮间的转向偏差，车辆在行驶过程中左右两侧的运动状态完全一致。因此，建立二自由度车辆模型作为参考模型，如图1所示。

图1 二自由度车辆模型

对车辆的动力学进行分析，列出动力学方程

(1)

其中

(2)

式中，Lf和Lr分别代表质心到前轴和后轴的距离；δf和δr分别代表前轮和后轮的转向角；αf和αr分别代表前轮和后轮的侧偏角；Ff和Fr分别代表前后轴轮胎侧向受力；Cαf和Cαr分别代表前后车轮的侧偏刚度；vy为车辆的侧向速度；β为车辆的质心侧偏角；γ为车辆的横摆角速度；m为车辆质量；Iz为转动惯量。

将式(2)代入式(1)中，整理可得4WS二自由度车辆模型的状态方程

(3)

1.2 七自由度车辆模型

本文研究4WS车辆在运动过程中的稳定性，以横摆角速度和质心侧偏角作为参考量。根据横参考模型求得的参考量的最优值与模型的值对比后求得偏差量[4]。考虑到车辆的纵向、侧向和横摆3个自由度的运动，再加上4个车轮的转动，建立七自由度车辆模型作为研究对象，如图2所示。

图2 七自由度车辆模型

根据所建立的七自由度车辆模型建立车辆动力学方程，假设车辆行驶过程中左右两侧轮胎的侧偏角相等，且不考虑轮胎之间的差异，公式为

(4)

(5)

(6)

其中，Fxij为车辆行驶过程中x方向上轮胎的受力；Fyij为车辆行驶过程中y方向上轮胎的受力；u为车辆纵向速度；ψ为车身横摆角。

2 控制算法

4WS车辆在转向行驶的过程中，随着速度增加或者转向半径减小，车辆的稳定性降低。为了能使车辆继续保持稳定的状态，通过监测车辆的横摆加速度来判定车辆的状态。如图3所示，通过观测车辆在相识过程中的横摆角速度和质心侧偏角，利用二自由度参考模型来得到车辆实际行驶过程中观测值的偏差量，判定车辆行驶的稳定状态。当车辆处于失稳的状态时，采用线性二次最优控制的方法，对横摆加速度和质心侧偏角的偏差值进行调控，求得所需要调控的横摆转矩。将调控横摆转矩通过PID控制分配到每一个车辆上，利用算法将横摆转矩转化成对四轮转向角。通过转向角的变化，来实现对横摆加速度和质心侧偏角的调控，从而使车辆保持稳定。

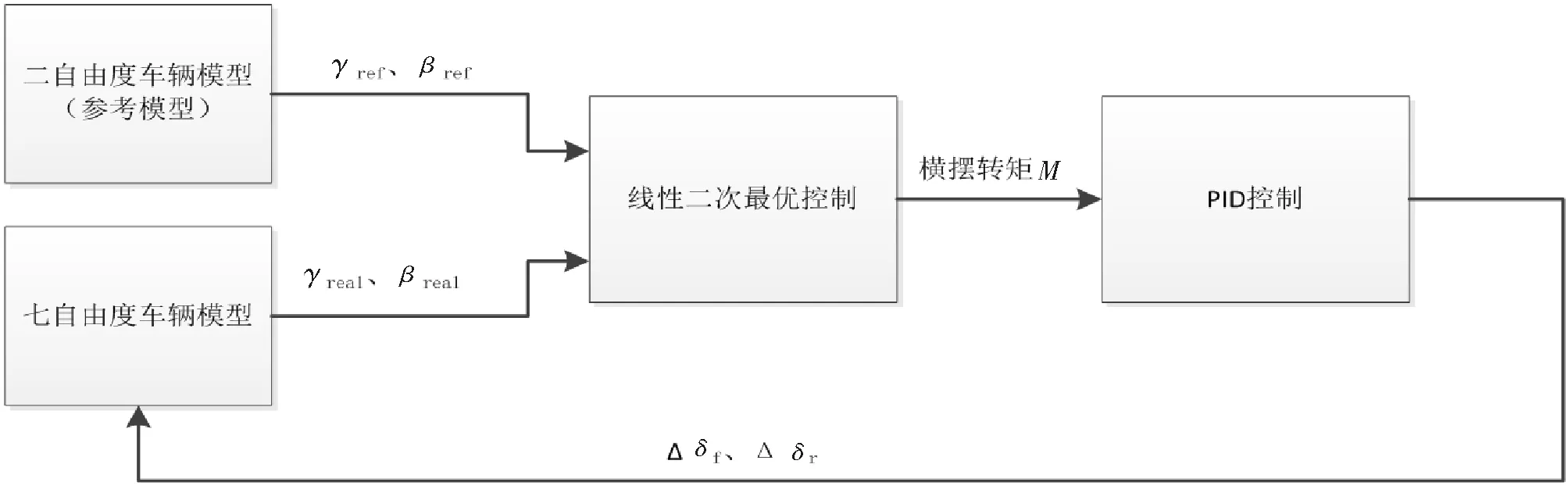
图3 控制算法流程图

图3中，γref、βref分别为由二自由度参考模型求得的横摆角速度和质心侧偏角的参考值；γreal、βreal分别为由七自由度车辆模型求得的横摆角速度和质心侧偏角的实际值；Δδf、Δδr分别为4WS车辆前轮转角和后轮转角的调控量。

2.1 线性二次最优控制

利用七自由度车辆模型求得车辆实际运行的横摆角速度与质心侧偏角，与参考模型中的横摆角速度与质心侧偏角的标准值相比较，得到两者的偏差量。将横摆角速度、质心侧偏角、横摆角速度偏差和质心侧偏角偏差作为线性二次最优控制的输入值，即控制系统中的性能指标。忽略左右轮胎力之间的偏差。建立表达式

(7)

其中，q1～q4分别为各性能指标的加权系数，利用线性参数变化调整方法[4-5]，根据不同车速情况，通过多次重复试验调节qi的取值。

将性能指标J的表达式改写为矩阵形式

(8)

可得Q，R，N为

(9)

利用黎卡提方程可求解最优控制反馈增益矩

阵[5]，其形如式(10)所示，其中A、B为状态矩阵；Q、R为权矩阵；P为黎卡提方程解

PA+ATP-(PB+N)R-1(BTP+NT)+QC=0

(10)

根据控制系统中传感器任意时刻的反馈状态x(t)，可以求出最优调控横摆转矩Md。

Md=-IzKX(t)

(11)

K=BTP+NT

(12)

2.2 PID控制器设计

利用求解出的调控横摆转矩，需要将横摆转矩转化成对应每一个车轮的转向角变化。本文研究假设左右两侧的转向角变化量相同，通过PID控制，对横摆转矩在前后轮之间进行合理的分配。再将分配后的横摆转矩转化成车轮转角。根据转矩与转角之间的关系，确定PID控制器的比例、微分和积分的参数，即KP、KI和KD，控制流程如图4示。

图4 PID控制流程

3 仿真分析

本文在Matlab/Simulink中建立驾驶员模型[6]和道路模型来模拟车辆行驶的环境，利用参考模型和七自由度车辆模型模拟车辆行驶。根据某款真实车辆参数对模拟七自由度车辆模型中的参数进行定义。具体参数为m=2 045 kg，Iz=5 428 K，Lf=1.488 m，Lr=1.712 m，d=1.14 m，hg=0.54 m，Cf=46 560 N/m，Cr=24 955 N/m。仿真模拟车辆分别以30 km/h、60 km/h和90 km/h的速度在环岛道路上行驶，实时观测车辆的横摆角速度和质心侧偏角，比较控制系统开启和控制系统关闭两种状态下车辆的稳定系数。

如图5所示，车辆在3种不同速度下横摆角速度的仿真图。

图5 横摆角速度仿真图

如图5所示，当车辆以恒定转向半径匀加速运动时，在控制系统关闭的前提下，随着速度的不断增大，车辆的稳定性降低。车辆在30 km/h的速度行驶时，横摆角速度相对比较稳定，实际值与理论值的偏差不大。当速度达到60 km/h时，偏差量逐渐增大，在控制系统的作用下，车辆的横摆角速度变化还是相对比较稳定。当速度达到90 km/h时，横摆角速度迅速增大，车辆处于转向不足接近失稳的状态，此时控制系统开启，横摆加速度得到实时的校正，横摆角速度仍能够基本保持稳定的状态。因此可以看出，当控制系统开启，车辆的横摆角速度得到校正，在低速时，车辆行驶相对比较稳定，控制效并不是很明显。但当车辆处于高速运动时，车辆的稳定性下降，通过控制器控制车辆的效果很明显。

如图6所示，车辆在3种不同速度下质心侧偏角的仿真图。

图6 质心侧偏角仿真图

如图6所示，当速度不断增大时质心侧偏角发生线性变化，车辆达到稳定状态时，质心侧偏角保持稳定值不变。比较控制系统开启和关闭两种状态下的质心侧偏角。当控制系统关闭时，车辆质心侧偏角随着速度的增加变化率越来越大，当车辆处于低速时，质心侧偏角变化相对比较平稳，曲线最终都会收敛，只是随着速度增大，收敛的所需要的时间变长。说明速度增加，车辆的稳定性越低。当速度达到90 km/h时，质心侧偏角不再处于收敛点状态，此时车辆完全失稳。但当开启控制系统时，车辆质心侧偏角能够保持相对稳定的状态，并且速度越大，控制系统的效果越明显。当车辆失去稳定性的时候，在控制系统的作用下，车辆迅速恢复稳定状态行驶。

4 结束语

(1)将横摆角速度与质心侧偏角作为判定车辆稳定性的标准，根据控制将两者的偏差量转化成4WS的轮胎转向角偏差。实验证明，该方法具有比较明显的效果，车辆稳定性有所提高；

(2)车辆在不同的速度下运行，当速度比较低的时候，4WS车辆的自身的稳定性能比较高，控制算法的介入不是很明显。当速度比较大时，车辆的稳定性下降。通过控制器对车辆的控制，车辆能够迅速恢复稳定的状态；

(3)在转向运动的过程中，控制系统开启的情况下，车辆的横摆角速度和质心侧偏角的变化幅度比较小，稳定性较高。

[1] 殷国栋,陈南.4WS车辆μ综合鲁棒主动侧倾操纵性能控制[J].东南大学学报:自然科学版,2006,36(3):384-388.

[2] 汪东明.4WS汽车的硬件设计及操纵稳定性控制[D].南京:东南大学,2005.

[3] Ferencey V,Bugár M.Algorithms vehicle control stability for military systems with 4 WS[C].Paris:International Conference on Military Technologies,IEEE,2015.

[4] Shamma J S.Analysis and design of gain scheduled control systems[D].USA:Massachusetts Institute of Technology,1988.

[5] Rugh W J,Shamma J S.Research on gain scheduling[J].Automatica(S0005-1098),2000, 36(10):1401-1425.

[6] 郭孔辉,马凤军,孔繁森.人-车-路闭环系统驾驶员模型参数辨识[J].汽车工程,2002,24(1):20-24.

[7] 焦凤,陈南,秦绪柏.四轮转向汽车操纵动力学虚拟仿真分析[J].汽车工程,2004,26(1):5-8.

[8] 郭孔辉,轧浩.四轮转向的控制方法的发展[J].中国机械工程,1998(5):73-75.

[9] 屈求真,刘延柱,张建武.四轮转向汽车自适应模型跟踪控制研究[J].汽车工程,2000,22(2):73-76.

[10] 王洪礼,张锋,乔宇.汽车四轮转向系统的非线性控制[J].机械强度,2003,25(2):130-133.

[11] Yuhara N.A review of four-wheel steering studies from the viewpoint of vehicle dynamics and control[J].Vehicle System Dynamics,1989,18(1-3):151-186.

[12] Kanazawa H,Takatani,Teruhiko,et al. Four-wheel steering system for vehicle: EP, US4610328[P].1986.

[13] Yu S H,Moskwa J J.A global approach to vehicle control: coordination of four wheel steering and wheel torques[J].Journal of Dynamic Systems Measurement & Control,1994,116(4):659-667.

[14] 崔胜民.汽车系统动力学研究内容综述[J].山东理工大学学报:自然科学版,1995(4):32-34.

[15] 金伏生,王仲范.汽车系统动力学研究—系统运动方程的一种形式[J].武汉工学院学报,1993(4):1-8.

Study on Algorithm of Stability Control Based on 4-Wheel-Steering Vehicle

GONG Xuwei,SUN Tao

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China )

In order to improve the stability and maneuverability of four-wheel-steering vehicle, the steering angle combined with yaw rate and side slip angle was controlled. Meanwhile, the reference model, 7-DOF vehicle model, optimal controller model and PID control model were built and developed respectively. Simulations were carried out in Matlab/Simulink. The results show that the control algorithm can effectively improve the stability of the four-wheel-steering vehicle.

yaw rate;side slip angle;Matlab/Simulink;linear-quadratic regulator;PID;system modeling

2017- 01- 07

上海市科研创新基金(12ZZ145)

龚戌伟 (1991-)，男，硕士研究生。研究方向：汽车系统动力学等。孙涛(1974-)，男，博士，硕士生导师。研究方向：车辆系统动力学与控制。

10.16180/j.cnki.issn1007-7820.2017.08.013

TP391.9

A

1007-7820(2017)08-048-05