一种基于气动加载系统的控制器设计

杨 雷，白国振，朱灵康

(上海理工大学 机械工程学院，上海 200093)



一种基于气动加载系统的控制器设计

杨 雷，白国振，朱灵康

(上海理工大学 机械工程学院，上海 200093)

基于气动加载系统是非线性系统，文中提出一种观测器-自适应模糊滑模反演控制方案。先对系统动静模型分析，获得二阶SISO动态方程，并通过系统模型辨识加以证明动态方程的有效性，进而反演控制结合滑模控制推算出控制律，再利用自适应模糊控制对其动态方程中未知量的模糊逼近，引用自适应控制对系统不确定性的补偿，同时加入观测器谋求对系统延时的解决。利用Matlab分别在阶跃、正弦输入信号下进行仿真。通过PID控制与文中算法的比较，结果表明文中算法响应速度快,实现了系统的跟踪控制。

气动加载系统；模型辨识；反演控制；滑模控制；自适应模糊控制

本文提出观测器-自适应模糊滑模反演控制策略。首先对气动加载系统进行理论分析出一类单输入单输出(Single Input Single Output，SISO)动态方程，并对该系统通过开环控制获得的数据进行拟合和自回归历遍(Auto-Regressive eXogenous，ARX)处理，加以验证SISO动态方程的有效性。基于动态方程结合反演控制的各部分误差子系统动态方程和滑模控制的滑模函数推算出该系统的控制律，注意到控制律中有未知函数和不确定性因素，进而设计自适应模糊控制对未知函数的模糊逼近和自适应控制对不确定性因素的进行动态补偿，并考虑到气动加载是一种时滞非线性系统，存在延时问题，引入延时观测器弥补对该算法在延时问题的控制方案，以便应用在工程实践中[1-2]。最后将设计的控制器进行Matlab仿真，并与传统PID控制对比，结果表明本文控制算法的响应速度快，轨迹控制效果好，能解决延时问题，具有良好的工程实践意义。

1 气动制动器加载系统的动态模型

1.1 加载伺服控制系统试验台

本文所研究的气动加载系统是基于气压通轴制动器加载试验台的加载系统。如图1所示。

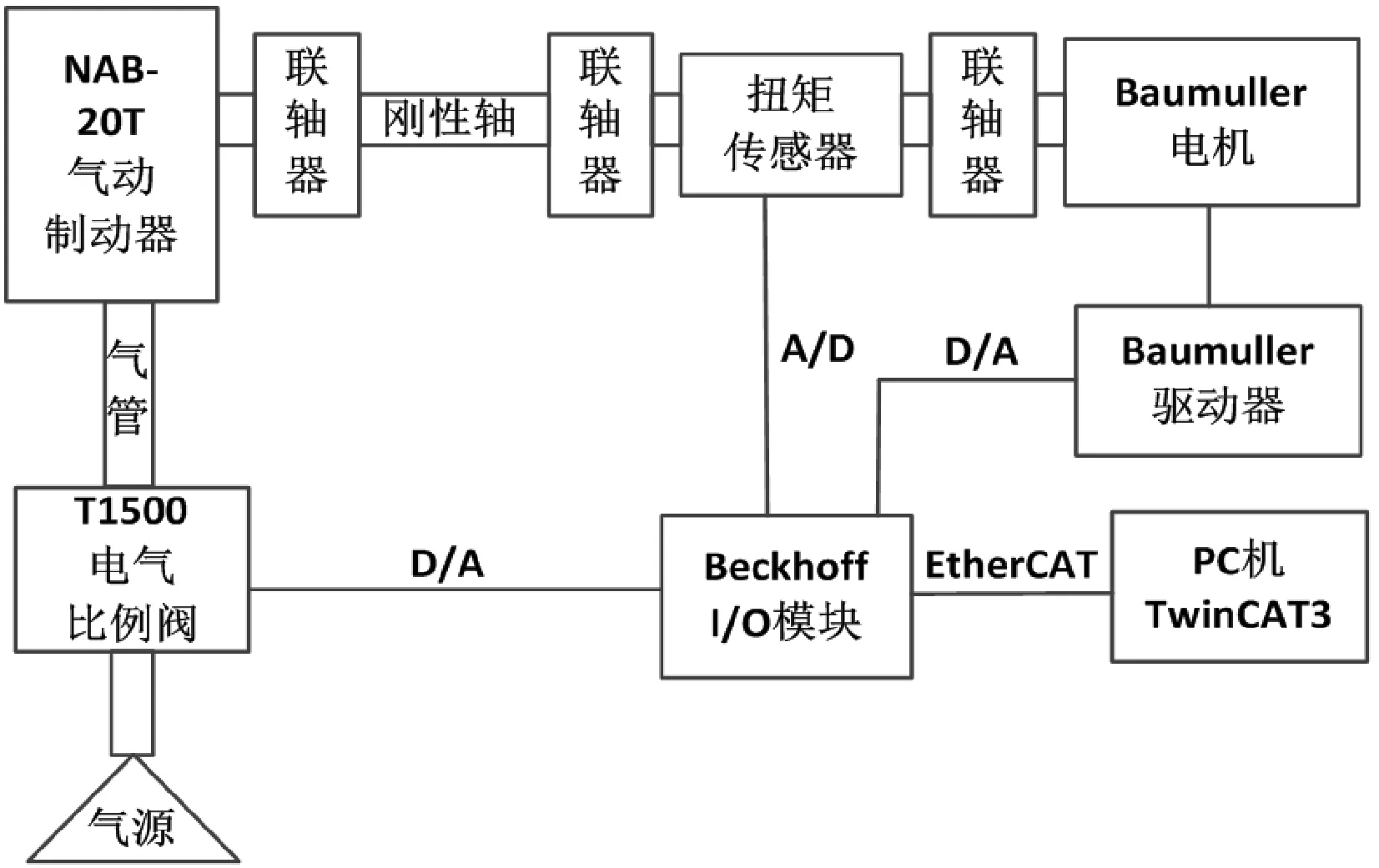
图1 气动加载试验台示意图

通过给定伺服电机恒定转速和电气比例阀的电压，以及控制气体流入气动制动器的气压，进而控制气动制动器的转矩；并结合扭矩传感器采集的信号作为为模拟量输入，与设定值比较获得误差，然后利用控制算法得到相应的控制量，实现设定值与实际测得值之差趋于零，图2所示为气动加载系统控制框图。

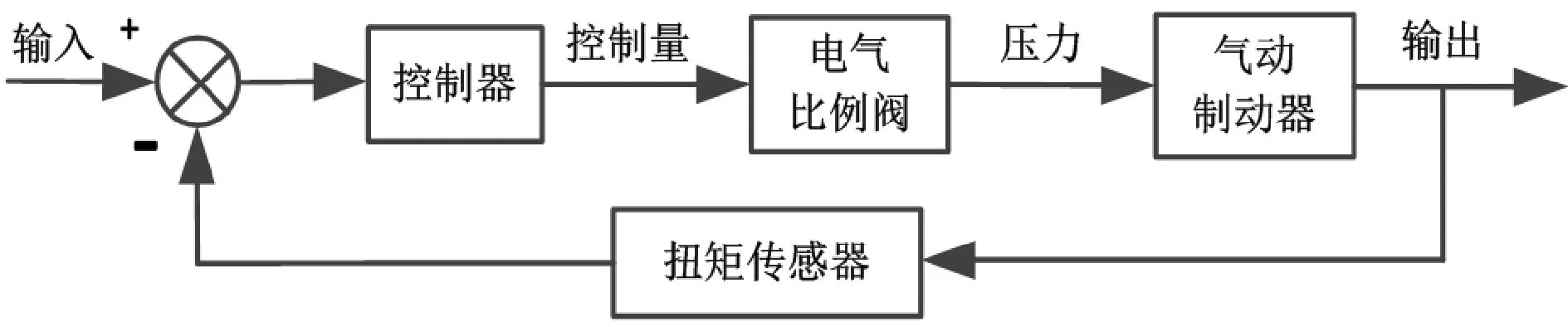
图2 气动加载系统控制框图

1.2 气压制动系统动态模型

文献[2]获得供气压力与气压传递终端关系即制动气室压力之间的关系。图3所示为气动加载系统简化示意图

(1)

(2)

式中，P1为气源的压力；T1为气源的温度；P2为制动管路的压力；T2为制动管路的温度；VL为制动管路容积；pc为制动气室内的压力；TC为制动气室内的温度；VC为制动气室内的容积；q1为控制阀的质量流量；q2为制动气室进气口质量流量。

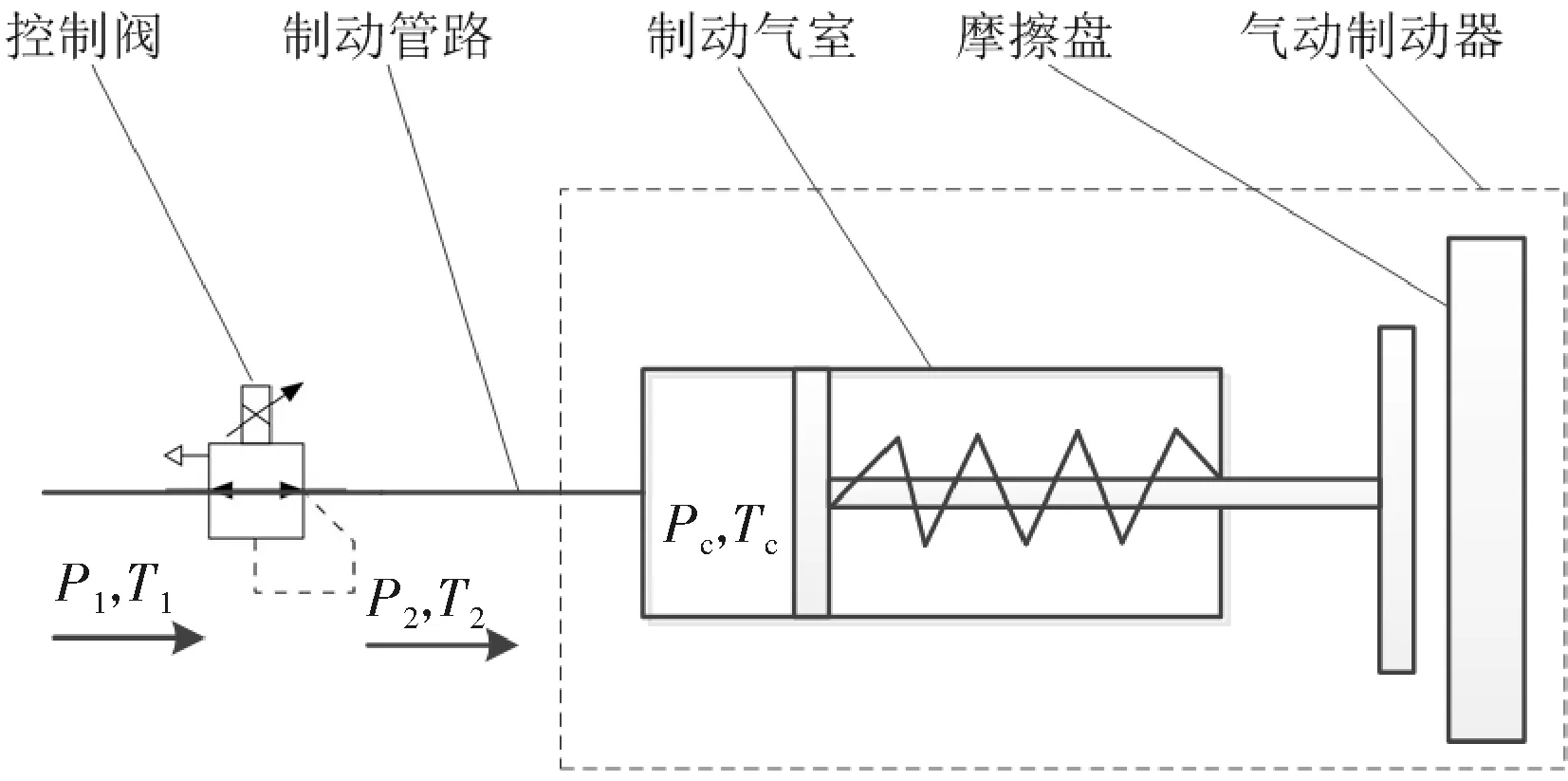
图3 气动加载系统简化示意图

进一步建立制动器部分模型，当制动气室内产生制动压力时，气室推杆推出，通过制动器的传动机构和力放大机构，将摩擦片推向摩擦盘，利用摩擦片与摩擦盘的摩擦力产生制动力矩从而实现扭矩加载[3]

(3)

式中，pc为制动气室的制动压力；pk为制动气室内克服弹簧弹力所需的气体压力；Ab为摩擦片的有效制动面积；Rb为盘式制动器的等效制动半径；Kb为制动器的效能系数；Tb为制动器产生的制动力矩。

显然，上述气动加载模型的可变参数和不确定性比较多,在实验中会引起显著的误差。基于搭建的实验平台，通过开环控制气动加载系统，标定出上述简化后的SISO数学模型，图4所示为气动加载系统的静态模型曲线拟合。

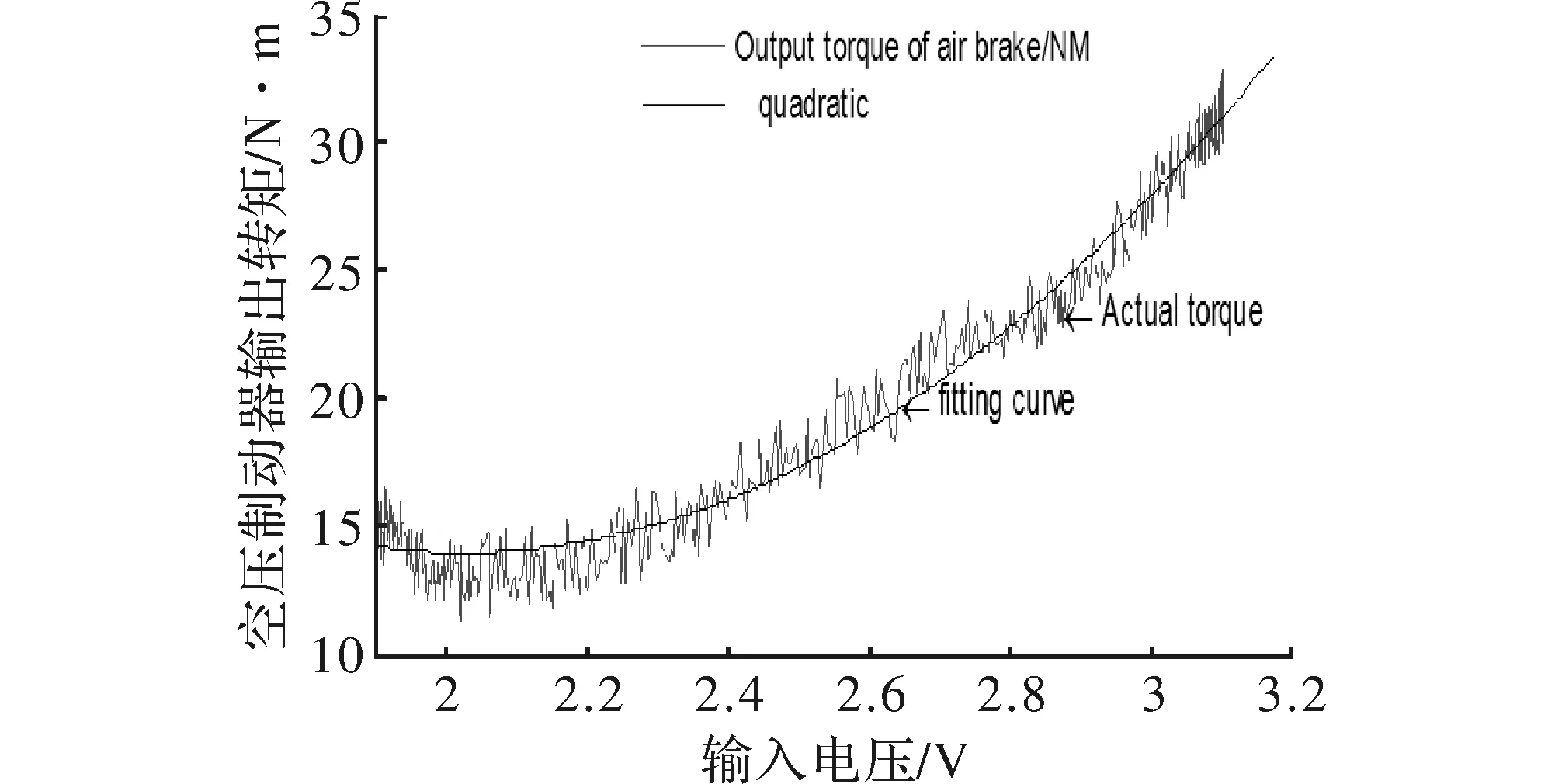
图4 气动加载系统的静态模型曲线拟合

基于上述实验数据，通过ARX模型并连续化后获得传递函数模型，该模型不仅反映比例阀本身，还反映来自于气缸中容积效应和加载气缸与摩擦盘等全局气动系统的等效模型，辨识结果为以下模型

(4)

结合文献[3]在气体均匀，气管等传递封闭性良好假设，描述气动加载系统的二阶模型，虽有一定的差异，但总体可以归纳为一类二阶系统。为便于研究，忽略温度、畸变摩擦等动态因素，归结为不确定因素方程类，即简化式为二阶SISO非线性动态方程

(5)

其中，f(Tb,t)，g(Tb,t)和d(Tb,t)为未知函数且有上界，为书写方便，分别简写为f,g,d。g≠0，|d|<δ,δ>0；Tb∈R2为单一输出转矩，q1∈R为单一控制阀的质量流量； 为系统的未建模部分和不确定部分。

2 控制器设计

2.1 模糊逼近系统

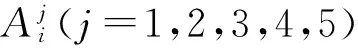
采用乘积推理机、单值模糊器和中心平均解模糊器，则模糊系统的输出为

(6)

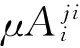
(7)

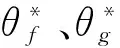
所以可定义模糊系统的逼近误差ε为

(8)

2.2 观测器-自适应模糊滑模反演制器设计

按照一般反演控制设计过程[6-7]，首先考虑基本反演设计控制器，基于上述SISO动态方程模型，定义系统误差如下

e1=Tb-yd

(9)

ei=Tbi-αi-1,i=2,3

(10)

其中，yd为输入指令；αi-1为待设计虚拟控制量。

第1步 对第一个误差子系统设计虚拟控制量

(11)

即推出第一个误差子系统动态方程为

(12)

第2步 对于第二个误差子系统设计虚拟控制量

(13)

即推出第二个误差子系统动态方程为

(14)

第3步 结合滑模控制器设计理论[14]，定义滑模面为

s=ce2-e1,c>0

(15)

(16)

得

(17)

第4步 设计控制律为等效控制ueq加上切换控制uvss。

u=eeq+uvss

(18)

即

(19)

式中，uvss用于实现不确定项和扰动的鲁棒性控制；h是正常数；δ为不确定项上界值；

sgn(s)为符号函数。

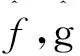
(20)

(21)

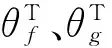
(22)

其中，r1、r2为正常数。对于式(20)中

(23)

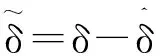
(24)

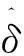
(25)

其中，r3为正常数。

第6步 在实际工程加载系统中有延时存在，故此引入延时观测器控制，即实际输出

xi(t)=Tbi(t-Δ)

(26)

式中，Δ为输出时间延时。基于式(5)动态方程，设计延时观测器为

(27)

同时上述系统误差式(9)和式(10)变为

(28)

(29)

图5 模糊滑模自适应控制总框

3 试验研究

结合文献[7]的传递函数作为被控对象进行Matlab系统仿真验证。设定阶跃扭矩指令为1 N·m;正弦扭矩指令为：幅值是1 N·m,周期是2π的正弦函数;且逼近函数f和g的模糊规则利用5种隶属函数对系统进行模糊化，即

(30)

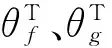
由响应波形曲线可以看出，即使设定值发生突变的情况下，观测器-自适应模糊滑模反演控制响应的波形可以快速跟踪上设定值，而在PID控制下的响应波形发生了比较慢的响应波形。即本文算法明显响应速度快，且与响应波形基本吻合。

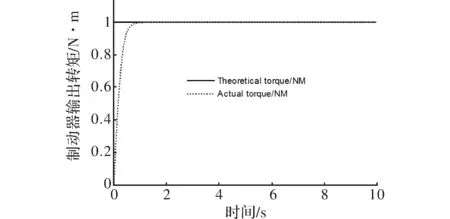
图6 PID控制阶跃响应曲线

图7 本文算法控制阶跃响应曲线

为验证本算法对延时的有效性，需进行正弦输入信号仿真，设计参数：c=11；k1=5；h=1.8；r1=0.7；r2=0.4；r3=0.2；Δ=3；基于上述参数初始化，分别通过PID(kp=11,ki=6,kd=1.5)和本文算法控制，获得仿真结果,获得Matlab仿真结果,如图8和图9所示的正弦跟踪曲线。

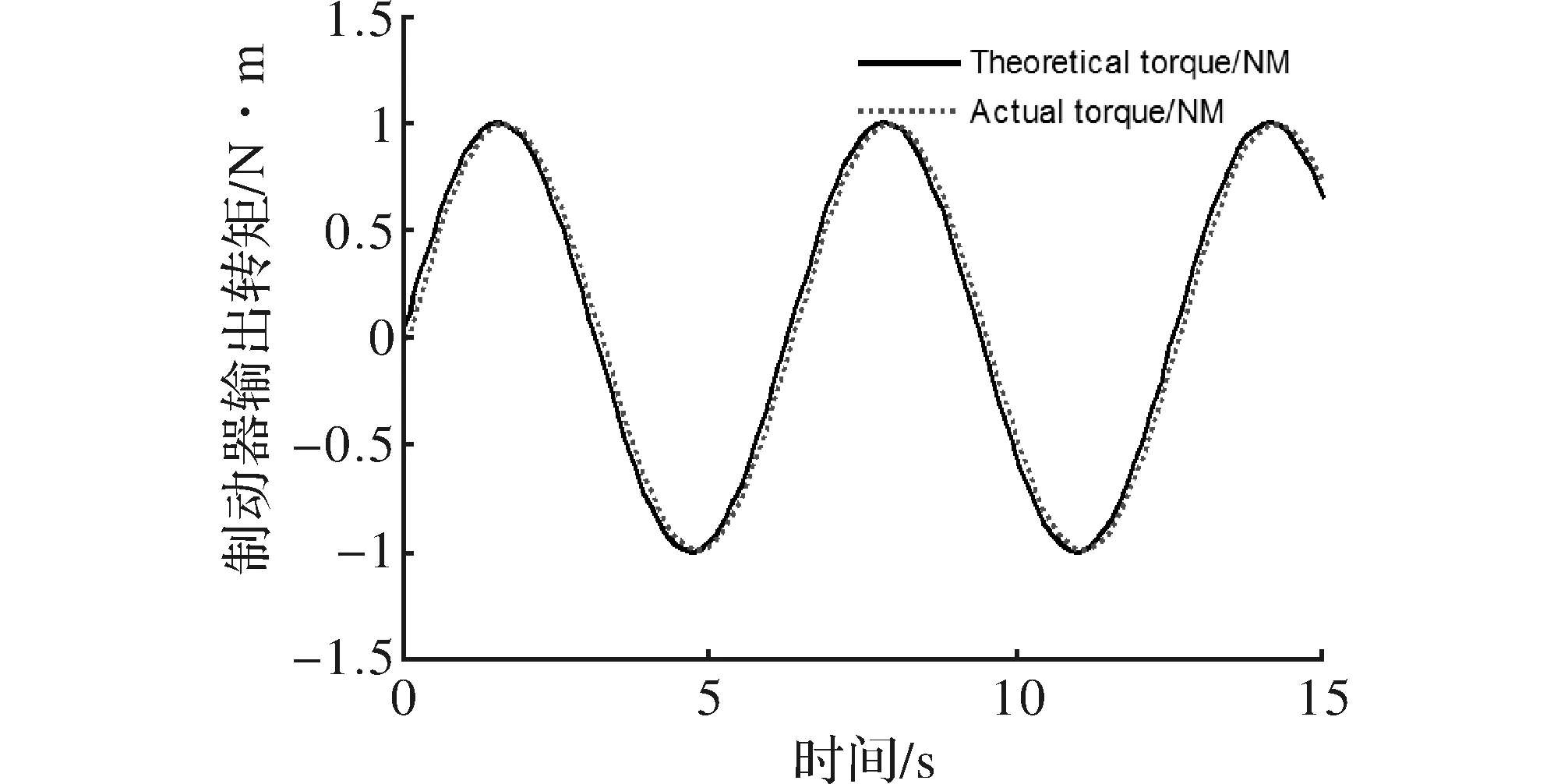
图8 PID控制正弦响应曲线

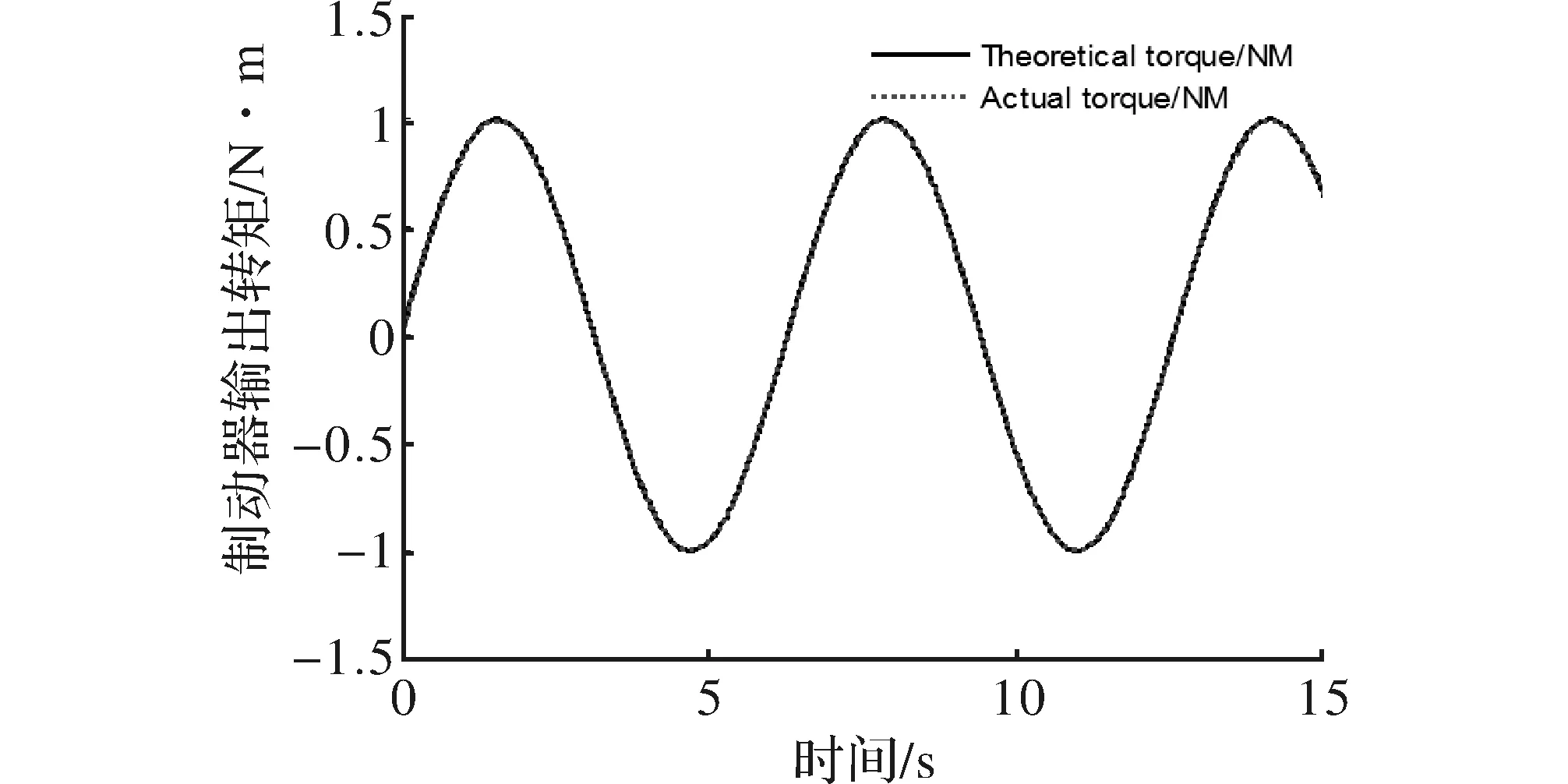
图9 本文算法控制正弦响应曲线

由响应波形曲线可以看出，在观测器-自适应模糊滑模反演控制下的响应波形可以解决延时问题和快速跟踪上设定值，且与响应波形基本吻合，而PID控制时，即使没有加延时模块时，其响应波形有一定的滞后性且未能较好的跟踪[10]。

4 结束语

本文针对气动制动器加载系统的非线性、延时及难以精确的建模等特点，提出一种观测器-自适应模糊滑模反演控制方案，通过Matlab仿真，从理论仿真上表明本文算法能够在短时间内快速响应调整，解决了加载系统的滞后问题。结果表明该控制算法响应速度快, 加载控制精度高，且解决延时问题，实现输出信号的轨迹控制。

[1] Das S,Bandyopadyay B,Paul A K,et al.Position control of pneumatic actuator using sliding mode control in conjunction with robust exact differentiator[C].Germany:Internationla Conference on Cntrol, Automation, Robotics, and Embedded System,2013.

[2] 王智深.客车气压制动系统欠压补偿控制技术研究[D].武汉:武汉理工大学,2012.

[3] 刘福才,贾亚飞,刘爽爽.气动加载系统的积分型线性自抗扰控制[J].控制理论与应用,2015(8):1090-1097.

[4] 刘福才,刘砚,徐文丽,等.气动加载系统的模糊自适应逆控制方法[J].机械工程学报,2014(14):185-190.

[5] 年珊珊,王学影,郭斌,等.气动模拟加载系统的模糊PID控制研究[J].组合机床与自动化加工技术,2014(3):123-126.

[6] 陈贵林,刘砚,徐文丽,等.基于数据驱动的气动加载系统在线建模方法[J].机床与液压,2013(3):12-16.

[7] 朱坚民,雷静桃,黄之文,等.基于灰色关联补偿控制的气动位置伺服控制系统[J].机械工程学报,2012(20):162-170.

[8] Prieto P J,Cazarez-Castro N R,Aguilar L T,et al.Fuzzy slope adaptation for the sliding mode control of a pneumatic parallel platform[J].International Journal of Fuzzy Systems, 2016(9):1-12.

[9] 侯小燕,薛文涛,李泰.气动弹性机翼的反演滑模控制[J].控制工程,2016(1):69-74.

[10] 覃秋松,麦云飞.模糊工程PID在气动位置伺服中的应用[J].电子科技,2015,28(11):104-109.

Controller Design Based on Pneumatic Loading System

YANG Lei，BAI Guozhen，ZHU Lingkang

(School of Mechanical Engineering,University of Shanghai for Science & Technology,Shanghai 200093,China)

The pneumatic loading system is a strong nonlinear system,an observer-adaptive fuzzy sliding mode inversion control scheme is proposed based on a nonlinear system with a pneumatic loading system. First, the system dynamic model is obtained, and the second order SISO dynamic equation is obtained. The validity of the dynamic equation is proved by identification of the system model. Inverse control is combined with sliding mode control to derive the control law. Then, the adaptive fuzzy control The adaptive control is used to compensate the uncertainties of the system, and the observer is added to solve the system delay. Finally, the simulation is carried out with step and sinusoidal input signals using Matlab. The results show that the proposed algorithm is fast in response and solve the problem of delay.

pneumatic loading system;model identification;inversion control;sliding mode control;adaptive fuzzy control

2016- 10- 25

杨雷(1992-)，男，硕士研究生。研究方向：信息处理等。

10.16180/j.cnki.issn1007-7820.2017.08.012

TP273

A

1007-7820(2017)08-044-05