小级数Ince-Gaussian光束光强模式分析

甄志强，马海祥，李新忠，李贺贺，王静鸽

(河南科技大学 物理工程学院，河南 洛阳 471023)

小级数Ince-Gaussian光束光强模式分析

甄志强，马海祥，李新忠，李贺贺，王静鸽

(河南科技大学 物理工程学院，河南 洛阳 471023)

研究了因斯-高斯(IG)光束级数m较小时，分立光瓣模式的光强分布。通过数值模拟，对IG奇偶模式以及奇偶模式线性叠加生成的PIG分立光瓣模式的光强进行了分析。分析结果表明：m较小时，PIG分立光瓣模式光瓣的空间位置介于奇偶模式之间，但是光瓣的光强分布变化较为明显。同一模式光瓣角向椭圆变量越接近于椭圆长轴，其光强比重越大。在统一总光强后，相同阶数与级数的不同模式光瓣总光强与角向椭圆变量差为一个三次函数的关系。对于偶模椭圆长轴上的光瓣，随着该模式通过PIGπ/2模式转化为奇模，该光瓣上的光强分布逐渐由弥散向着逆时针方向集中。

物理光学;因斯-高斯光束；模式分布；光场调控；微粒操纵；数值模拟;光强分析

0 引言

因斯-高斯(Ince-Gaussian，IG)模式[1]是空间近轴波动方程(paraxial wave equation,PWE)在椭圆坐标系上的准确正交解，是一种自然存在于稳定谐振腔中的激光模式。其模式分为奇模和偶模，因其与厄米特-高斯(Hermite-Gaussian，HG)模式和拉盖尔-高斯(Laguerre-Gaussian,LG)模式相比，具有更为丰富的模式分布，一直吸引着研究者的关注[2-13]。

2004年，文献[1]首次推导出PWE在椭圆坐标系下的准确正交解，提出了IG模式分布，并发现它是LG和HG的过渡模式，为IG光束提供了理论基础。同年，文献[14]在理论上发现IG光束的奇模和偶模线性组合可以生成椭圆形的涡旋光束，称为螺旋因斯-高斯(helical Ince-Gaussian，HIG)光束，丰富了涡旋光束的类型。文献[15]首次在实验上从稳定谐振腔中直接产生了IG模式，为IG光束奠定了实验基础。文献[16]使用液晶显示器产生了IG模式和HIG模式，降低了IG光束研究的实验成本。随后，IG模式与HIG模式相继在微操纵[7]、制备涡旋光束或涡旋阵列[3,17-18]等领域得到广泛应用。最近，为了进一步扩充IG光束在精细操纵领域的应用，基于IG光束的奇偶模式，文献[19]提出了一种具有初始相位调控的IG模式分布(the Ince-Gaussian beam with initial phase difference，PIG)。该模式大大丰富了IG光束的模式分布，实现了IG光瓣在椭圆轨迹上的精确位移控制，为IG光束在微粒操纵及光束微雕刻等领域提供了额外的调控自由度。然而，文献[19]仅研究了PIG模式光束级数m较大时的模式分布，而当m较小时，由于光瓣数量较少，光瓣上光强分布不均匀[1]，无法形成椭圆形的光瓣分布。此外，光强的分布直接影响微粒捕获应用中的光场梯度力的分布[20]，因此，对于IG模式光场分布的研究具有重要的意义。

PIG模式作为一种最近才提出的对精细操纵等领域具有潜在应用价值的IG光束模式分布，其分立光瓣模式的光强分布介于IG光束奇偶模式之间，因此，对于m较小时PIG模式分布的研究有助于解析IG光束各种光瓣模式的光强分布，在微操纵领域具有重要的研究意义。针对该问题，本文研究了m取值较小时，PIGπ/2模式与PIG3π/2模式的光强分布，以及其与IG光束奇偶模式光强分布的关系，并进一步探讨了IG光束各种光瓣模式的光强变化规律，为IG光束对微粒的精细操纵提供了理论依据。

1 PIG光束的产生方法

考虑在椭圆参数为ε的椭圆坐标系下，IG光束奇偶模式的表达式[1,14]为：

(1)

(2)

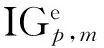
具有初始相位差的IG光束的奇偶模式叠加，生成的PIG模式电场表达式[19]为：

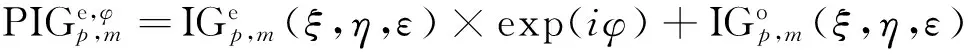
(3)

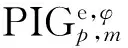
2 结果与讨论

PIG光束的产生采用数值模拟的方法，对PIG模式及其与IG奇偶模式的关系进行可视化研究。模拟中，选取参数λ=532nm，椭圆参数ε=2，传播距离z=375mm，采样间隔为0.05mm。

图1为p=m=1时，PIG分立光瓣模式以及IG奇偶模式的归一化光强分布图。图1中虚线为计算出的光瓣最亮点的连线；虚线旁边的角度为虚线与水平线的夹角。由图1可以看出：p=m=1时，这4种模式均为两个光瓣对称分布，光瓣上的光强分布十分稳定，即4种模式的变化过程中，每个光瓣上的光强分布无变化。计算出的这4条连线夹角为45°，由此可知，该状态下，PIG分立光瓣模式相当于IGe模式或IGo旋转45°时对应的模式光强分布，符合文献[19]中提到的PIG模式光强分布规律，但是由于模式的光瓣数量较少，无法形成光瓣在椭圆轨迹上的精确位移调控。

图1 p=m=1时，种模式光强分布图

下面分析p=m≠1时的模式光强分布情况。图2为p=m=2,3时，4种模式的光强分布图。图2a～图2d依次为p=m=2时，IGe、PIGπ/2、IGo、PIG3π/24种模式的光强分布；图2e～图2h依次为p=m=3时，以上4种模式的光强分布。对比图2a与 图2c、图2e与图2g可以看出：IGe模式光瓣数比IGo模式减少了m-1个。观察图2a、图2b、图2e、图2f可以发现：当IGe模式过渡到PIGπ/2时，光瓣绕中心逆时针旋转了一定的角度，IGe中心的光瓣上下两部分在这种运动趋势中逐渐被分离。观察图2b、图2c、图2f、图2g可以发现：最终过渡到IGo时，光瓣完全分离。因此，由PIG模式提供了IGe与IGo模式变化的中间状态，证明了对于p和m相等且较小时，IGe模式中心光瓣其实是上下两个光瓣连在一起形成的。另外，由图2c、图2d、图2g和图2h可以看出：IGo模式到PIG3π/2模式的变化为光瓣继续逆时针旋转，上下相互拉近的两光瓣形成了连接的趋势。从图2a、图2d、图2e、图2h中可以看出：最后重新过渡到IGe模式，相当于IGe到IGo模式之间的逆变换。不同的是两个过程变换方向均为逆时针，使得PIGπ/2模式与PIG3π/2模式不同且相互对称。另外，4种模式光瓣光强分布均满足如下规律：光瓣越是靠近光强分布椭圆的长轴(简称椭圆长轴)，其总光强越大。该规律命名为光瓣间的光强分布规律。值得注意的是，这4种模式均为IG光束的模式，下面通过对p=m=3时，IG光束这4种模式光瓣光强的精确求解，来研究IG光瓣间光强分布的统一规律。

图2 p=m=2,3时，PIG模式与模式光强分布图

为了表示光瓣与图片左右两边的距离，定义椭圆角向变量差△η为光瓣光强分布极大值的角向椭圆变量与0或π(椭圆长轴的角向椭圆变量)差值的最小值。另外，模拟求解中，选取最大光强的1/5作为光瓣范围的阈值。为了使该研究具有现实意义，假设4种模式在同一个光路中产生，且产生4种模式的衍射效率一样，即4种模式分布的总光强一样。在以上假设下，以p=m=3为例，绘制了IG模式光瓣总光强Iall与光瓣椭圆角向变量差△η的关系图，如图3所示。使用多项式拟合的方法，求解出光瓣总光强与光瓣椭圆角向变量差的关系为Iall=8 225△η3-17 296△η2+3 974△η+7 671，其拟合度R2=0.985 97≈1，说明计算出的参数与方程拟合得非常好，验证了该方程的准确性。光强分布决定着光场梯度力的大小，该研究有助于预测IG的4种模式变换时力场分布的变化，对微粒操纵具有指导意义。

图3 IG模式光瓣总光强与光瓣椭圆角向变量差的关系

针对p≠m时的情况进行研究。图4以p=4，m=2为例，展示了IGe、PIGπ/2、IGo、PIG3π/24种模式的光强分布图，依次对应于图4a～图4d。此时，光瓣的空间位置为内外两环的分布状态[1]。对于内环光瓣，其变化趋势与图2中p=m时的情况相似，不再做重复分析。对于外环，由于光瓣数量较少，使得IGe模式在椭圆长轴上的光瓣分布范围较大，光强较为弥散。由图4a和图4b可以看出：当过渡到PIGπ/2模式时，光瓣逆时针运动，同时，长轴上光瓣的光强分布向着逆时针的方向集中。对比图4b和图4c可以看出：过渡到IGo时，两光瓣光强完全流入其中一端，形成一个光强较为集中的光瓣。该光强变化规律命名为光瓣内部的光强变化规律。对于其他光瓣，由于光瓣本身光强分布集中，因此光强变化忽略不计。而原先偶模时在椭圆短轴上的光瓣，在该变化中光强逐渐变大，其规律等同于p=m时光瓣间的光强变化规律。

图4 p=4，m=2时，PIG模式与模式光强分布图

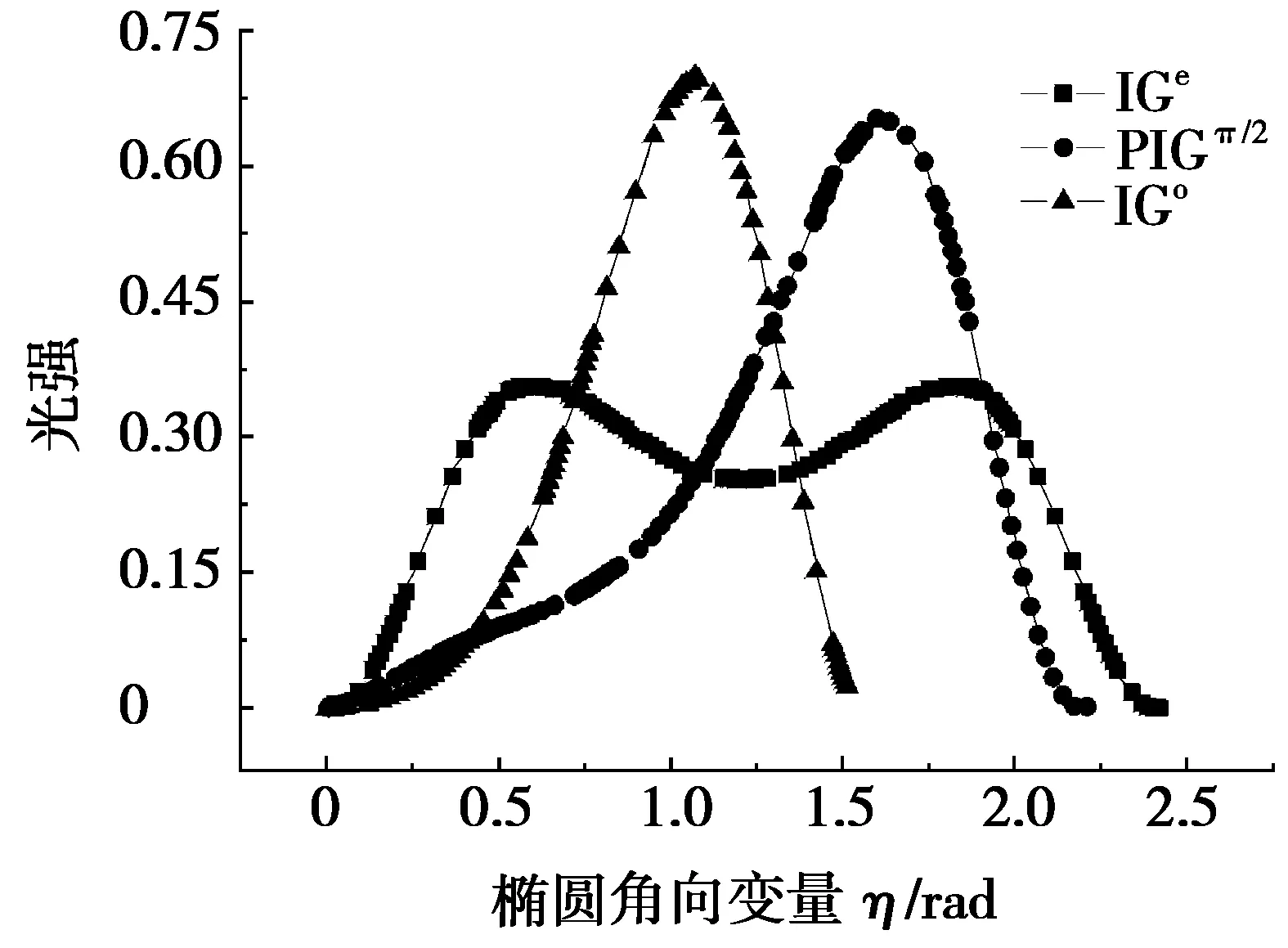
图5 椭圆节点线上最左端光瓣光强分布

为了了解光瓣上力场的变化，定量研究PIGπ/2模式与IGe、IGo模式光瓣上的光强分布。选取IGe椭圆长轴的一个光瓣为研究对象，将图4中最左端光瓣在其所在的椭圆节点线[19]上的光强分布取出，绘制图5。图5中，横坐标为选取的光瓣样本初始点定为0点的椭圆角向变量。由图5中可以看出：3种模式中IGe模式的光强峰值最小，光强分布范围最大。IGo模式光强峰值最大，光强分布范围最小。验证了3种模式变化过程中，光强分布在逐渐地集中。另外，对于IGe模式，其弥散的光强分布使得光瓣上形成了两个光强峰值。变化过程中，左边峰值消失。该现象在双微粒的聚集调控中有潜在应用价值。

3 结论

使用数值模拟的方法研究了光束级数m较小时，PIG分立光瓣模式与IG奇偶模式的光强分布。4种模式的切换规律与文献[19]相符，即PIG分立光瓣模式为奇偶模式的中间状态。另外，得到IG光束同一模式中光瓣间的光强变化规律，即光瓣越是靠近椭圆长轴，其总光强越大。在统一各模式总光强后，所有模式光瓣光强分布与定义的光瓣椭圆角向变量差为三次函数的关系。此外，光瓣内部的光强变化规律为：由IGe模式通过PIGπ/2模式到IGo模式的变化过程中，IGe模式椭圆长轴光瓣逐渐由弥散的光强分布向逆时针方向集中。

[1]BANDRESMA,GUTIERREZ-VEGAJC.Ince-Gaussianbeams[J].Opticsletters,2004,29(2):144-146.

[2]BANDRESMA,GUTIERREZ-VEGAJC.Ellipticalbeams[J].Opticsexpress,2008,16(25):21087-21092.

[3]CHUSC,YANGCS,OTSUKAK.VortexarraylaserbeamgenerationfromaDoveprism-embeddedunbalancedMach-Zehnderinterferometer[J].Opticsexpress,2008,16(24):19934-19949.

[4]GUTIERREZ-VEGAJC.Characterizationofellipticdarkhollowopticalbeams[C]//DigestoftheLeosSummerTopicalMeetings.2008:7-8.

[5]ALPMANNC,WOERDEMANNM,DENZC.Tailoredlightfields:InceGaussianbeamsoffernovelopportunitiesinopticalmicromanipulation[C]//ConferenceonLasers&Electro-OpticsEurope,IEEE.2011.

[6]BAIZY,DENGDM,GUOQ.ElegantInce-Gaussianbeamsinaquadratic-indexmedium[J].Chinesephysicsb,2011,20(9):094202.

[7]WOERDEMANNM,ALPMANNC,DENZC.OpticalassemblyofmicroparticlesintohighlyorderedstructuresusingInce-Gaussianbeams[J].Appliedphysicsletters,2011,98(11):111101.

[8]PARRA-HINOJOSAA,GUTIERREZ-VEGAJC.FractionalInceequationwithaRiemann-Liouvillefractionalderivative[J].Appliedmathematicsandcomputation,2013,219(22):10695-10705.

[9]LEIJ,HUA,WANGY,etal.AmethodforselectiveexcitationofInce-Gaussianmodesinanend-pumpedsolid-statelaser[J].Appliedphysicsb(lasersandoptics),2014,117(4):1129-1134.

[10]FORBESA,LIZOTTETE,MELLADO-VILLASENORG,etal.ExperimentalgenerationofHermite-GaussandInce-Gaussbeamsthroughkinoformphaseholograms[C]//SPIEOpticalEngineeringApplications,InternationalSocietyforOpticalEngineering.2015.

[11]HANS,LIUY,ZHANGF,etal.DirectgenerationofsubnanosecondInce-Gaussianmodesinmicrochiplaser[J].LEEEphotonicsjournal,2015,7(1):4500206.

[12]RENYX,FANGZX,GONGL,etal.DynamicgenerationofInce-Gaussianmodeswithadigitalmicromirrordevice[J].Journalofappliedphysics,2015,117(13):133106.

[13]PENGY,CHENB,PENGX,etal.Self-acceleratingAiry-Ince-GaussianandAiry-helical-Ince-Gaussianlightbulletsinfreespace[J].Opticsexpress,2016,24(17):18973-18985.

[14]BANDRESMA,GUTIERREZ-VEGAJC.Ince-Gaussianmodesoftheparaxialwaveequationandstableresonators[J].Journaloftheopticalsocietyofamericaa,2004,21(5):873-880.

[15]SCHWARZUT,BANDRESMA,GUTIERREZ-VEGAJC.ObservationofInce-Gaussianmodesinstableresonators[J].Opticsletters,2004,29(16):1870-1872.

[16]BENTLEYJB,DAVISJA,BANDRESMA,etal.GenerationofhelicalInce-Gaussianbeamswithaliquid-crystaldisplay[J].Opticsletters,2006,31(5):649-651.

[17]KENJUO,SHU-CHUNC.Generationofvortexarraybeamsfromathin-slicesolid-statelaserwithshapedwide-aperturelaser-diodepumping[J].Opticsletters,2009,34(1):10-12.

[18]CHUN-FUK,SHU-CHUNC.Numericalstudyofthepropertiesofopticalvortexarraylasertweezers[J].Opticsexpress,2013,21(22):281-288.

[19] 马海祥，李新忠，李贺贺，等.相位差因子调控的Ince-Gaussian光束空间模式分布研究[J].光学学报,2017,37(6):0626002.

[20]WOERDEMANNM,ALPMANNC,ESSELINGM,etal.Advancedopticaltrappingbycomplexbeamshaping[J].Laser&photonicsreviews,2013,7(6):839-854.

国家自然科学基金项目(61205086,11504091)；瞬态光学与光子技术国家重点实验室开放基金项目(SKLST201203)；河南省高等学校青年骨干教师资助计划基金项目(2013071)

甄志强(1978-)，男，河南林州人，实验师，主要从事光场调控及散斑测量技术方面的研究.

2017-02-18

1672-6871(2017)06-0086-05

10.15926/j.cnki.issn1672-6871.2017.06.017

O436；O438.1

A