基于双层粒子群算法的下级渠道流量不等时渠系优化配水

刘 照，程 帅，李华朋，姜春雷，刘春悦，丁小辉，张树清

(1.中国科学院东北地理与农业生态研究所， 吉林 长春 130102； 2.中国科学院大学， 北京 100049；3.聊城大学环境与规划学院， 山东 聊城 252000； 4.吉林建筑大学测绘与勘察工程学院， 吉林 长春 450001)

基于双层粒子群算法的下级渠道流量不等时渠系优化配水

刘 照1,2，程 帅3，李华朋1，姜春雷4，刘春悦1，丁小辉1,2，张树清1

(1.中国科学院东北地理与农业生态研究所， 吉林 长春 130102； 2.中国科学院大学， 北京 100049；3.聊城大学环境与规划学院， 山东 聊城 252000； 4.吉林建筑大学测绘与勘察工程学院， 吉林 长春 450001)

以黑河中游张掖市甘州区盈科灌区盈四支一分支为研究对象，在现有渠道优化配水模型基础上，针对下级渠道配水流量不相等的情况，对渠系优化配水工作进行研究。选择以渠道输水损失最小与轮灌组间引水持续时间差异值最小建立多目标优化配水模型，以下级渠道出水口的开关状态与实际流量为决策变量，采用双层粒子群算法求解最优轮灌组合。成功构建了下级渠道不等时的渠系优化配水模型，采用双层粒子群算法求得的结果表明，轮灌组划分合理，下级渠系流量变化范围在其设计流量的[74.3%～77.6%]，上级渠系流量变化平稳，最大配水时间113.4 h，其结果低于人工制定的168 h原配水计划。各渠道流量在其允许的范围内变化，渠系优化配水过程与配水时间组合合理，上级渠道配水流量均匀，避免了上级渠系流量突然变化与减少对下级渠系的影响,不仅减少了渠道弃水，同时使各个轮灌组同一时间关闭，有效减少了闸门调节次数，为灌区管理部门制定配水计划提供决策。

渠道流量；不等流量；双层粒子群算法；优化配水

渠系优化配水是指在配水渠道及其下级渠道过水能力一定的条件下，为满足灌区农作物某次灌水的要求，采取一定的方法与技术，对配水渠道轮灌组合进行优化。作为水资源优化配置领域一个重要的研究方向，科学合理的渠系优化配水决策可以减少渠系输水过程中的渗水损失和无效弃水，对提高水分利用率和提高粮食产量有着重要的意义。

对于配水渠道的组合优化而言，国内外学者对渠系优化配水模型和决策方法进行了大量研究，提出了众多模型，求解模型的方法也经历了由线性规划、动态规划等到智能算法的演变[1-5]。张智韬等[6]将3S技术应用到渠系优化配水模型研究中，建立以轮灌组引水持续时间差异最小为目标函数，采用蚁群算法来替代传统的遗传算法对模型进行求解,提高了优化效果；为了解决更深入、复杂的问题，许多新型优化智能算法被广泛使用，模型的建立也不仅仅为单一的目标，多目标配水模型也被考虑进来。张国华等[7]采用以总的配水时间最短和轮灌组引水持续时间差异最小为多目标函数，并采用粒子算法对模型进行求解，所得结果略优于现有的其它方法；高伟增等[8]以轮期内所有配水时段上、下级渠道的输水渗漏损失总量最小和总配水时间最少及配水时间差最小为目标建模，并采用多目标复合智能算法对模型进行求解，其结果不但减少了渠道弃水，而且还减少了人工管理的劳动时间。但上述方法都是在下级渠道流量相等的情况下对模型进行解算，在求出轮灌组合后进行轮灌组时间的均一化处理。由于实际情况的复杂性，多数情况下级渠道流量并不相等，一些研究学者在这方面做了大量的研究，算法上也逐步改进。马孝义等[9]在下级渠道引水流量不等情况下建立渠系优化配水模型，并采用标准遗传算法对模型进行求解，减少了渠系输水渗透损失。赵文举等[10-11]也对下级渠道流量不相等的情况进行了研究，同时采用自适应遗传算法和模拟退火遗传混合算法对优化模型进行求解，结果表明较基本遗传算法，利用改进的遗传算法和混合遗传算法可以显著地提高计算稳定性和加快解集收敛速度。Pawde等[12]考虑到渠系实际运行中各下级渠道流量约束的不同，改进了Wardlaw[3]等建立的模型，并利用粒子群算法解算出最优轮灌组合。张国华等[13]同时考虑了上级配水渠道断面变化以及下级被配水渠道流量不等的情况，建立了精细化的优化配水模型，并利用自由搜索算法对模型进行求解，结果表明配水过程更加平顺均匀，有效减少了闸门调节次数和无效水量损失。基于上述研究，遗传算法在求解渠系优优配水模型上虽具有遗传算法的优点和全局搜索性能较强等特点，但其搜索速度慢，容易出现早熟等问题，本文在下级渠道流量不相等的情况下，基于粒子群算法自身的优势，在现有的粒子群算法进行渠系优化配水模型的基础上进行改进，采用双层粒子群算法进行渠系优化配水模型算法的设计与结算，求解轮灌组的同时，直接进行轮灌组时间的均一化处理，减弱了由于地形、作物种植结构、外界条件的不同与变化，对渠道优化配水的影响，减少了配水时间，提高渠系优化配水工作的效率和精度。

1 优化配水模型的建立

传统的优化配水模型将各出水口按“定流量、变历时”的工作方式进行流量调度以获取最优轮灌组合方案，本文则是将各出水口按“变流量，变历时”的运行方式进行渠系优化配水。

1.1 轮灌组划分

设上级配水渠道的引水设计流量为Qs(m3·s-1)(不包含配水渠道的输水损失)，其上有N个出水口(即配水渠道)，各出水口引水设计流量为qj(m3·s-1)，其中j=1,2,…，N。出水口以qj引取水量所需的时间为tj，其中j=1,2,…，N。则轮灌组的划分数为：

(1)

式中，M为轮灌组个数；Qs为上级配水渠道的引水设计流量；q平均为下级各出水口设计流量的平均值；ceil为向上取整函数；floor为向下取整函数。

1.2 决策变量

(1) 以轮灌组出水口的开关状态为决策变量Xij(下标i=1,2,…M为轮灌组序数；j=1,2,…,N为出水口序数)，Xij∈{0，1}，Xij=0表示出水口关闭，Xij=1表示出水口开启。

1.3 目标函数1

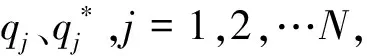
Z=min(Vsu+Vsd)

(2)

式中，Z为输水损失总量，Vsu、Vsd分别为轮期内上下两级渠道的输水损失总量(m3)；据文献[8-9]

(3)

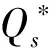
(5)

从式(5)中知，Au、mu、Vu、Lu、Aj、mdj、Lj、Vj为定值，由此可以近似认为：在渠道输水总量、输水工作长度、渠床土壤性质及衬砌方式、地下水深及出流条件确定情况下，渠道输水损失水量随渠道流量增大而减小。要想减少渠道输水损失，必须在满足渠道流量安全约束条件下(在渠道设计流量的0.6～1.0倍之间变化时[9])，增大上、下级渠道的流量，流量越大输水损失就越小。

1.4 目标函数2

一些研究学者认为进水闸调节次数最小[4]，意味着各轮灌组引水持续时间尽可能接近，即各轮灌组引水持续时间差异最小，使得配水渠道进水闸尽可能在同一时间关闭，以各轮灌组引水持续时间差异ΔT最小为目标函数,可用式(6)表示。

(6)

式中，Ti、Tk分别为第i、k轮灌组的引水持续时间(h)。

1.5 约束条件

(1) 轮期时间结束：每一轮轮灌组内所有出水口的轮流引水时间不超过配水渠道最大允许输水时间。即有：

(7)

式中，T为配水渠道最大允许输水时间(h)。

(2) 出水口约束状态：任一个出水口在所有轮灌组内只能开启一次，即有：

(8)

(3) 决策变量取值约束：

Xij∈{0，1}，(i=1,2,…,M,j=1,2,…,N)

(9)

(4) 下级渠道配水流量约束：任一下级渠道的配水流量应在其设计流量的0.6～1.0倍以内。

(10)

(11)

2 基于双层粒子群算法的模型设计与求解

2.1 双层粒子群算法

双层粒子群算法是一种基于双层模型的粒子群优化算法，是分层分群粒子群算法中的最基本算法。基本粒子群算法有1个N维空间构成，每一个粒子在自身认为最佳寻优路径和群体最佳寻优路径的影响下朝着最优解的方向移动[14]。针对渠系下级流量不等配水模型的特点，本文采用双层粒子群算法求解模型。双层粒子群算法由两层结构组成，分别称为顶层和底层[15]，如图1所示，顶层为渠系层，底层为流量层。在流量层先给定一个决策变量，渠系层以这个决策变量为参量，根据目标函数和约束条件，在可能的范围内求解一个最优解，渠系层将自己的最优解反馈给流量层，流量层在可能的范围内求得整体最优解，顶层和底层交互迭代，同步优化上、下层，最终求得双层模型的全局最优解，保证算法的同时得到高质量的解和较快的收敛速度。在每一次迭代过程中，渠系层或流量层中的粒子都是通过跟踪两个“极值”来更新自己。一个是粒子本身所找到的最优解，即个体极值；另一个是该层内整体种群目前找到的最优解，称为全局解。粒子在找到上述两个极值后，根据下面公式(12)的两个公式来更新自己的速度与位置。假设在渠系层或流量层有N维搜索空间，共M个粒子组成粒子群，其中第i个粒子在N维搜索空间中的位置是Xi，记Xi=(Xi1，Xi2,…XiN)，则每个粒子的位置就是一个潜在的解。将Xi带入目标函数就可以计算出其适应度值，根据适应度值的大小衡量Xi的优劣。第i个粒子的“飞翔”速度也是一个N维向量，记为Vi=(Vi1,Vi2，…ViN)。记第i个粒子迄今为止搜索到的最优位置为Pi=(Pi1,Pi2…PiN)，该层所有粒子迄今为止搜索到的最优位置为Pg=(Pg1,Pg2…PgN)。PSO算法的更新方程如下：

Vin更=Vin+C1r1(Pi-Xin)+C2r2(Pg-Xin)；Xin更=Xin+Vin更

(12)

式中，i=1,2,…,M，M为粒子的个数；n=1,2…,N，N为搜索空间维度；C1和C2为学习因子，取非负数；r1和r2为介于[0，1]之间的随机数；Vin∈[-Vmax，Vmax]，Vmax为常数。

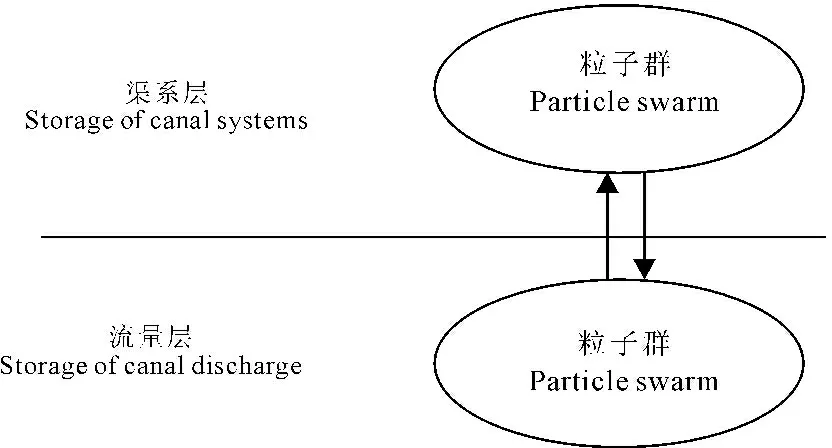
图1 双层粒子群算法

2.2 模型求解的双层粒子群算法

2.2.1 粒子的编码 针对渠系优化配水模型的特点，用向量对粒子进行编码，对函数优化问题或有约束的优化问题是有效的，即把每种粒子编码成N维向量。

对粒子采用向量的编码方法(Block Mouth=BM=斗口，Canal Discharge=CD=渠道流量),渠系层的粒子Particle1=(BMk，BMk，…，BMk，…BMk)，流量层的粒子Particle2=(CDk，CDk，…，CDk，…CDk)(K=1，…，N，1-N为正整数但不能重复)。例如Particle1=(6,3,16,11,7,17,14,8,5,19,15,1,2,4,18,13,9,20,10,12)为一个粒子，对应(六斗，三斗，十六斗，十一斗，七斗，十七斗，十四斗，八斗，五斗，十九斗，十五斗，一斗，二斗，四斗，十八斗，十三斗，九斗，二十斗，十斗，十二斗)；Particle2=(CD1,CD2,CD3,CD4, CD5,CD6,CD7,CD8,CD9,CD10,CD11,CD12,CD13,CD14,CD15,CD16,CD17,CD18,CD19,CD20)，对应的(一斗，二斗，三斗，四斗，五斗，六斗，七斗，八斗，九斗，十斗，十一斗，十二斗，十三斗，十四斗，十五斗，十六斗，十七斗，十八斗，十九斗，二十斗)的实际流量。

2.2.2 适应度函数的构造 适应度函数要能反映渠道轮灌优化配水模型中渠道输水损失最小(公式(5))和各轮灌组间引水持续时间差异最小(公式(6))。该多目标问题采用权重系数变化法，将各个目标函数线性加权求和并求其倒数构造出适应度函数，为了避免 和 在数量级别上的相差，构造适应度函数即：

(13)

式中，particle为计算的粒子；α为权重系数，可采用层次分析法等确定，W=灌水定额×支渠水权面积；灌水定额为1 200 m3·hm-2，支渠水权面积为234.47 hm2。

2.2.3 约束条件的处理方法 本算法采用修复不可行解法，借助一些修复方法，按照某种原则，将随机产生和粒子飞行过程中产生的不可行解全部或部分用可行解代替。

3.3 Bi-PSO算法的寻优过程

(1) 初始化Bi-PSO算法的参数，随机产生满足底层约束条件的初始解粒子的位置Xi和速度Vi，满足顶层约束条件的初始解位置Yj和速度Vj。

(2) 计算F(Xi,Yj)的初始目标函数值，比较粒子的适应度，并将最优适应度值对应的粒子分别作为底层、顶层初始全局最优粒子。

(3) 利用式(12)对底层、顶层两层粒子更新迭代。同时采用底层和顶层交互迭代的方法，同步优化[16-17]。作为初始粒子的第一次迭代，其个体最优就是粒子本身，之后则采用其在解空间移动时所经历的最好点。

(4) 判断更新后底、顶两层粒子是否满足约束条件，如不满足对其进行修复。

(5) 计算更新后粒子F(Xi,Yj)适应度值，比较并记录底层、顶层两层粒子的个体最优位置和全局最优位置。

(6) 判断找到的全局最优解是否达到收敛条件或最大迭代次数，如果满足条件，则已得到了模型的最优解，输出结果，如果不满足则转到③。

3 实例应用

3.1 与其它方法的比较

为了验证方法的可靠性，与其它优化配水模型进行对比，本文选用陕西冯家山灌区北干十一支渠24条斗渠2005年春灌某轮期的配水资料进行计算，得到优化结果与文献[9-11]的优化结果进行对比，文献[9-11]都是以灌溉过程中水量损失最小为目标函数，本文是以水量损失最小和轮灌组引水时间差异最小为目标函数，由表1可以看出本模型输水损失量更小，配水时间更短。

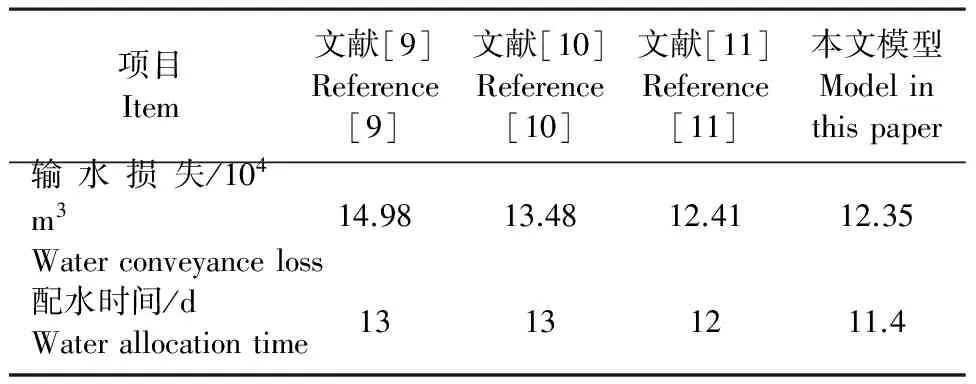
表1 文献[9-11]优化结果与本研究结果对比

3.2 应用实例

3.2.1 研究区概况 盈科灌区位于黑河流域中游(海拔1 400～1 600 m之间)是黑河流域水资源的主要消耗区。灌区东西长25.4 km,南北宽14.2 km,总面积为197.8 km2，地势较为平坦，多年平均温度6℃～8℃，年降水量104～328 mm，时间上多集中在5—9月，其降雨量占全年的80%～90%，年潜在蒸发量1 638～2 341 mm，蒸发强烈，降水稀少，土壤以灰棕漠土为主。灌区内有3条主要干渠，支渠31条，斗渠256条，农渠、毛渠等若干。如图2所示(本数据由“黑河生态水文遥感试验(HiWATER)”产生)[18]。

3.2.2 模型优化结果 张掖市甘州区盈科灌区盈四支一分支传统经验方法所制定的夏灌三轮配水计划时间为2012年6月17日8时至2012年6月24日8时，轮灌期为T=7 d(168 h)。如图2所示，图中特指的部分为实例分析的盈四支一分支渠和其下属的20条斗渠，一分支渠的设计流量Qs=0.7 m3·s-1，其下属各斗渠的设计流量qj=0.3 m3·s-1。(本数据由“黑河生态水文遥感试验(HiWATER)”产生)[18]。同时采用双层粒子群算法对已经构建好且经过实例化的多目标渠系优化配水模型进行解算，双层粒子群算法的详细参数设置如表2所示，计算结果如表3、表4，图3所示。

结果表明：如表3、4所示，将盈四支一分支渠下属的20个斗渠划分为3个轮灌组，轮灌组划分合理，每个组的引水时间均为113.4 h，同时斗渠的优化配水流量在其设计流量的74.3%～77.6%之间变化，符合斗渠设计流量的变化范围，配水过程更加平顺均匀，有效减少了闸门调节次数和无效弃水；如图3所示，将每个时间段内的斗渠优化后的流量相加，得到支渠流量变化。支渠内流量变化稳定，在[0.68,0.7] m3·s-1之间内变化，说明优化的结果合理。

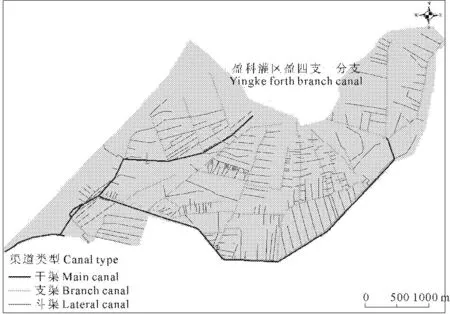
图2 盈科干渠盈四支一分支及其下属斗渠

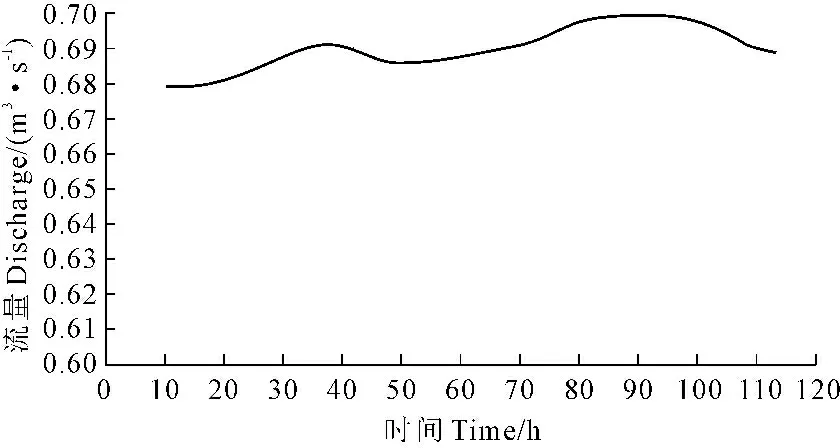
图3 支渠流量变化图

表2 双层粒子群算法的参数设置

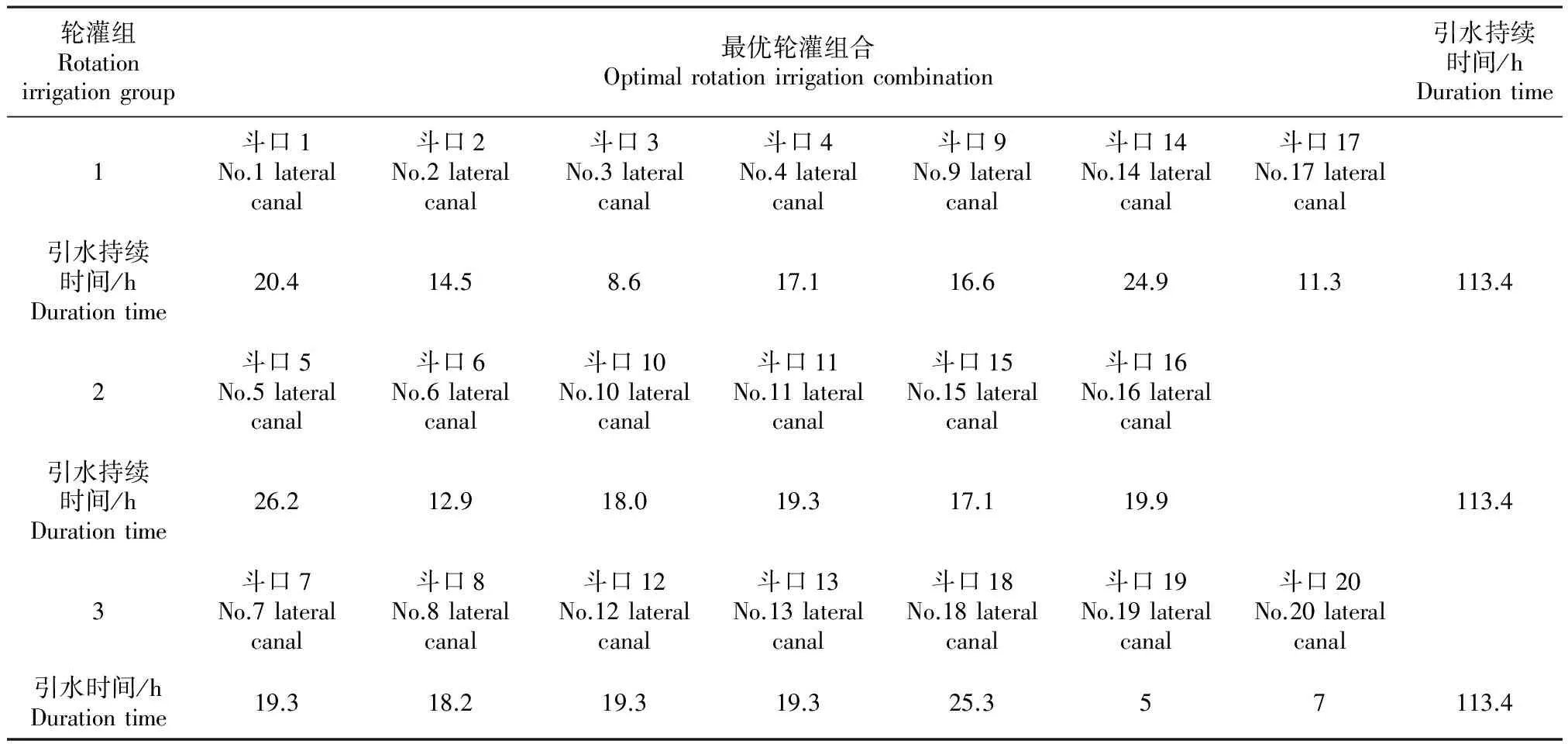
表3 研究对象最优轮灌组合

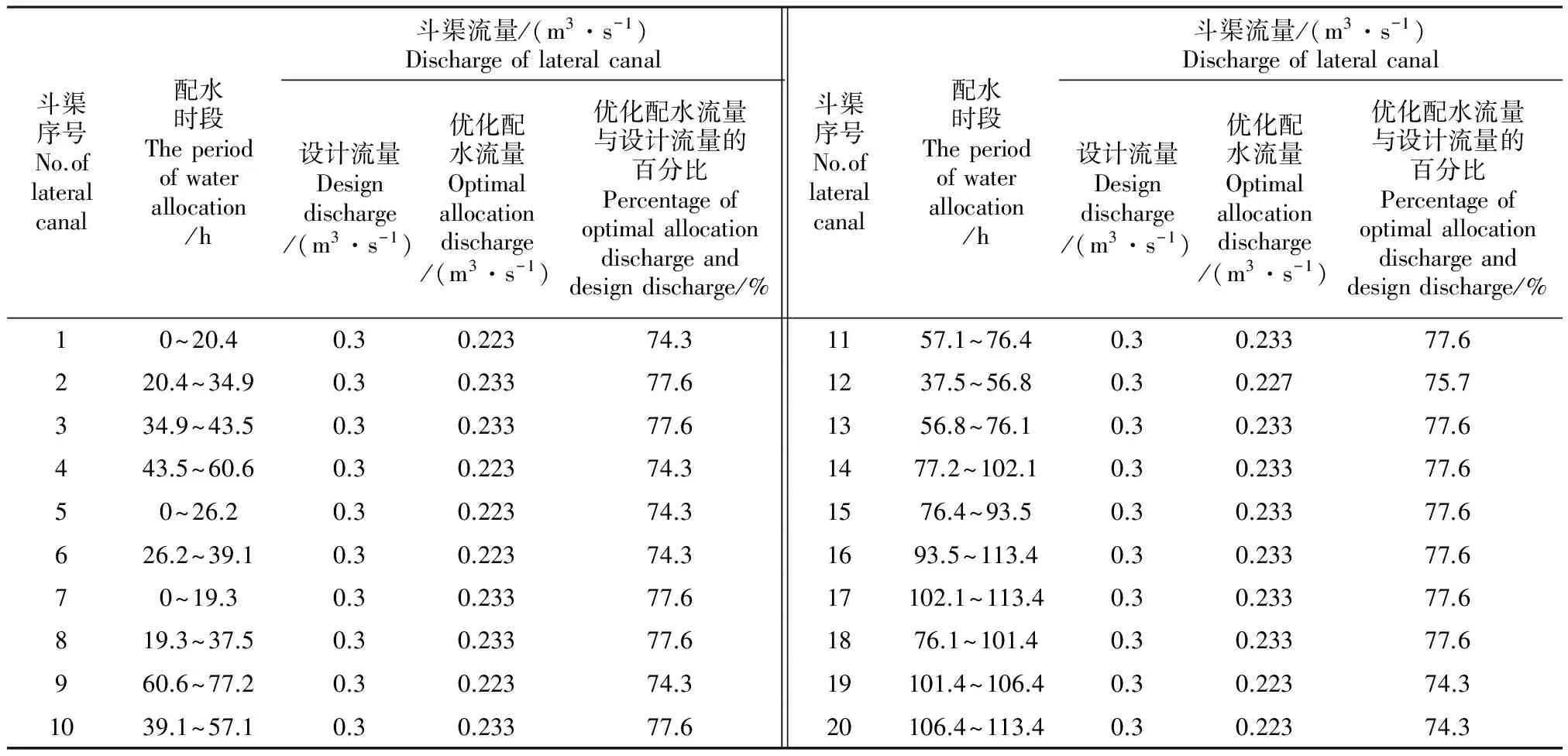
表4 斗渠优化配水过程时间与流量表

注：配水时段的0时为2012年6月17日8时配水计划开始时间。 Note：The beginning of water distribution is at 8am, June 17, 2012.

4 讨论与结论

张掖市甘州区盈科灌区是位于黑河中游的典型灌区，从灌区的地理位置、气象条件、土地利用情况看，总体来说盈科灌区控制的灌溉区域属于干旱地区，是典型的内陆干旱气候，灌区缺水问题严重，同时存在水资源利用率不高等问题。本文的研究结果减少了灌溉输水时间和渠道的输水损失，并通过冯家山灌区对文章中的算法及其模型进行验证，说明本文的方法具有一定的现实意义。同时经实地考察轮灌组划分合理，研究结果与灌区实际配水情况基本吻合，为黑河中游灌区管理提供一定的理论依据。但该模型没有考虑到灌溉用水的蒸散发量是动态变化的，以及将地表水-地下水-农作物生长耦合模型应用到模型研究中，同时该渠系优化配水模型仅在支渠和斗渠的两级渠道上建立与求解，所构建的模型存在一定的局限性，所以该模型在多级渠系优化配水与耦合其它模型上都有待进一步完善。

渠系优化配水是水资源优化配置领域一个重要的研究方向，本文构建了下级渠道流量不等时的优化配水模型，采用双层粒子群算法，将渠系层和流量层分开，降低了下级渠系流量不等时建立模型的复杂性，采用向量的方式对粒子进行编码，符合人们的思维习惯，从而使算法设计变得方便。实例结果表明将盈四支一分支渠下属斗渠分成3个轮灌组，与实地调研盈科灌区灌溉配水时轮灌组划分情况相吻合，轮灌组划分的数目较少，减少了上级渠系流量突然变化与减少对下级渠系配水情况的影响，配水质量得到提高，以期为灌区水管所水管站等管理部门制定配水计划提供决策。

[1] Reddy J M, Wilamowski B, Cassel-Sharmasarkar F C. Optimalscheduling of irrigation for lateral canal[J]. ICID (S1531-0353), 1999,48(3):1-12.

[2] 吕宏兴,熊运章,汪志农.灌溉渠道支、斗渠轮灌配水与引水时间优化模型[J].农业工程学报,2000,16(6):43-46．

[3] Wardlaw R, Bhaktikul k. Comparison of genetic algorithm and linear programming approaches for lateral canal scheduling[J]. J Irrig and Drain Engrg, 2004,130(4)：311-317.

[4] 宋松柏,吕宏兴.灌溉渠道轮灌配水优化模型与遗传算法求解[J].农业工程学报,2004,20(2):40-44.

[5] Peng S Z, Wang Y, Khan S, et al. A simplified multi-objective genetic algorithm optimization model for canal scheduling[J]. Irrig Drain, 2012,61(3):294-305.

[6] 张智韬,李援农,陈俊英,等.基于3S技术和蚁群算法的灌区渠系优化配水[J].西北农林科技大学学报(自然科学版),2010,38(7):221-226.

[7] 张国华,张展羽,邵光成,等.基于粒子群优化算法的灌溉渠道配水优化模型研究[J].水利学报,2006,37(8):1004-1008,1014.

[8] 高伟增,赵明富,汪志农,等.渠道轮灌配水优化模型与复合智能算法求解[J].干旱地区农业研究,2011,29(6):38-42.

[9] 马孝义,刘 哲,甘学涛.下级渠道流量不等时渠系优化配水模型与算法研究[J].灌溉排水学报,2006,25(5):17-20.

[10] 赵文举,马孝义,刘 哲,等.基于自适应遗传算法的渠系优化配水模型研究[J].系统仿真学报,2007,19(22):5137-5140.

[11] 赵文举,马孝义,张建兴,等.基于模拟退火遗传算法的渠系配水优化编组模型研究[J].水力发电学报,2009,28(5):210-214,113.

[12] Pawde A W, Mathur Y P, Kumar R. Optimal water scheduling in irrigation cananl network using particle swarm optimization[J]. Irrigation and Drainage, 2013,62:135-142.

[13] 张国华,谢崇宝,皮晓宇,等.基于自由搜索算法的灌渠配水优化模型[J].农业工程学报,2012,28(10):86-90.

[14] Kenndey J, Eberhart R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks. Perth Australia, 1995:1942-1948.

[15] Chen Chiachong. Two-layer particle swarm optimization for unconstrained optimization problems[J]. Applied Soft Computing, 2011,11(1):295-304.

[16] 李昌兵,张斐敏.基于层次粒子群算法的配送中心双层规划选址策略[J].兰州理工大学学报,2013,39(4):105-109．

[17] 赵志刚,王伟倩,黄树运.基于改进粒子群的双层规划求解算法[J].计算机科学,2013,40(11):115-119.

[18] 盖迎春,庄金鑫,徐凤英,等.黑河生态水文遥感试验：黑河流域中游渠道流量测量数据集[G].兰州:中国科学院寒区旱区环境与工程研究所,2012.

OptimalwaterallocationincanalsystemunderunequaldischargesinsubordinatecanalsbasedonBi-levelPSOMethod

LIU Zhao1,2, CHENG Shuai3, LI Hua-peng1, JIANG Chun-lei4, LIU Chun-yue1, DING Xiao-hui1,2, ZHANG Shu-qing1

(1.NortheastInstituteofGeographyandAgroecology,ChineseAcademyofSciences,Changchun130102,China; 2.UniversityofChineseAcademyofSciences,Beijing100049,China; 3.SchoolofEnvironmentandPlanning,LiaochengUniversity,Liaocheng,Shandong252000,China; 4.CollegeofSurveyingandProspectingEngineering,JilinArchitectureUniversity,Changchun,Jilin450001,China)

Taking No.1 Sub-branch Canal of the Yingke Forth Branch Canal in Ganzhou Region of Zhangye City located in middle reach of the Heihe River as the research object, based on the present canal optimal water allocation model, aimed at the situation of unequal discharge in subordinate canals, carried out research of optimal water allocation in canal system. Selected the minimal water losses by canal water delivery and minimal time difference among rotation groups, set up the multi-objective optimal water allocation model. Taking the switch state of the subordinate canals and actual discharge as the decision variables, the optimal combination of rotational irrigation group has been solved by using the Bi-level PSO Method. The optimal water allocation model in canal system was successfully constructed under unequal discharge in subordinate canals. The result obtained by using the Bi-level PSO Method has been showed: The rotation irrigation groups were divided rational. It suggested that the discharge at lateral canal of change range was 74.3%～77.6% and the discharge of branch canal was flowed smoothly, the maximal water allocation time was 113.4 h, which was less than the 168 h in original water allocation plan constituted by hand. Each canal discharge was changed within the allowable range, the allocation time combination in the process of optimal water allocation in canal system was rational. The allocated discharge in superior canal was equalization to avoid the effects of discharge suddenly change in superior canal to the subordinate canals. Not only the surplus water in canals was decreased, meanwhile let each irrigation rotation group was close in same time, the gate regulating times were effectively reduced, the decision-making can be provided for the irrigation management division to draw up the water allocation plan.

canal discharge; unequal discharges; Bi-level PSO Method; optimal water allocation

1000-7601(2017)03-0088-06doi:10.7606/j.issn.1000-7601.2017.03.14

2016-09-02

：2017-03-20

：国家重点研发计划“全空间信息系统与智能设施管理”项目(2016YFB0502301)

刘 照(1991—)，男，辽宁阜新人，硕士生，研究方向为灌区信息化系统，GIS智能计算。 E-mail:liuzhao@iga.ac.cn。

张树清(1964—)，男，吉林白山人，研究员，博士生导师，主要从事3D/4D地理信息系统理论建模、分析、计算和遥感信息提取。 E-mail:zhangshuqing@neigae.an.cn。

S274.3

： A