基于SIFT算法的全景图像拼接技术研究①

文伟东, 张 明

(上海海事大学 信息工程学院, 上海 201306)

基于SIFT算法的全景图像拼接技术研究①

文伟东, 张 明

(上海海事大学 信息工程学院, 上海 201306)

全景图像拼接技术即通过将部分重叠区域的图像合成以描述某个场景信息的360度圆形图像. 引用一种新型的基于SIFT(尺度不变特征变换)特征匹配的图像排序算法, 实现图像的有序排列, 针对图像拼接存在的误匹配点较多、耗时较长等问题, 结合FAST算法进行特征点提取, 接着针对相邻有序图像间的亮度差异采用自动校正操作,削弱了相邻图像间的亮度差异, 并结合改进的Ransac算法剔除误匹配点对, 最后用加权平衡算法实现图像的快速融合. 实验结果表明该优化排序算法稳定、高效.

全景图像拼接; 图像排序; 自动校正; 加权平衡; 融合

图像拼接技术作为一大研究热点, 主要用于计算机视觉和数字图像处理领域. 图像拼接技术即是将同一场景下的两个或多个重叠图像通过一系列数字图像技术处理[1], 并且可以获得包含所有原始图像信息的新的全景图像. 近年来, 该技术被广泛应用于航天, 医学,虚拟现实和日常生活等许多领域. 图像配准即是找到两个或更多个图像的重叠部分, 并建立图像之间的关系.图像配准算法可以大致分为两种类型[2], 一种是基于图像特征的图像配准, 另一种是基于区域的图像配准.

基于特征的图像配准通过使用图像中匹配的局部不变特征来确定图像之间的几何变换关系. 1977年Moravec提出了角点特征和称为“兴趣点”的概念. 他通过灰度自相关函数来思考该像素和其领域像素的相似性. 1988年, Harris改进了Moravec角, 并提出了Harris角点检测算法. 继lindeberg提出了尺度空间理论之后, Mikolajczyk和Schmid提出了具有尺度不变特征的Harris-Laplacian检测算子和Harris-Affine检测算子. 2000年, Lowe[3]提出了高效SIFT(尺度不变特征变换)局部特征, 成为局部特征研究领域的里程碑.

文中引用一种基于SIFT特征提取的新型图像排序算法. 在该方法中, 匹配特征首先通过计算一个图像和其它图像之间的匹配点的数量来获得最近的图像, 并逐一计算, 以最终获得精确的图像顺序, 同时结合了高效的FAST算法获取高斯金字塔图像中的特征点对, 从而提升算法的运行效率; 接着针对有序相邻图像间的亮度差异, 实行相邻图像的亮度差异校正操作, 同时结合改进地Ransac[4]算法剔除错误匹配点对, 最后用加权平衡算法实现图像的快速融合. 最终实现高质量、稳定的全景图像.

1 特征点提取

1.1 SIFT特征点提取

1999年, David G. Lowe教授总结了现有的基于不变技术的特征检测方法, 并在此基础上提出尺度不变特征变换SIFT-图像局部特征描述算子. SIFT基于尺度空间, 并且保持对图像变换的不变性, 例如缩放, 旋转和仿射变换. 并于2004年得到进一步改进.

SIFT特征提取和匹配的过程主要包括四个部分:SIFT特征检测, SIFT特征描述, SIFT特征匹配和匹配点提纯. 具体步骤如图1所示.

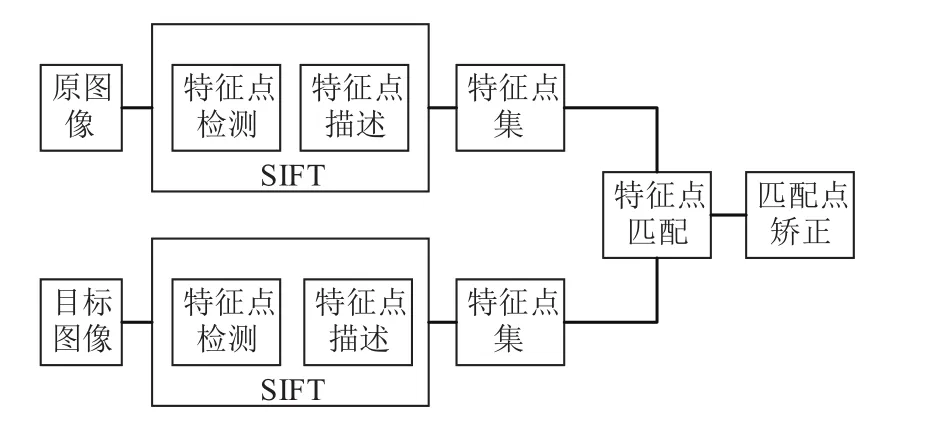
图1 SIFT特征检测和匹配的流程图

SIFT特征提取的过程按如下顺序: 极值检测, 精确定位特征点位置, 计算特征点的主方向以及特征描述符生成.

SIFT算法通过在不同尺度空间上寻找关键点, 高斯模糊是获取尺度空间的理论支撑[5], 即依据高斯模板和原图像做卷积运算, 实现模糊图像. N维空间的正态分布表示为:

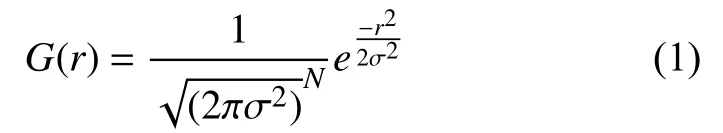
假设二维高斯模板大小视为m×n, 那么可得出模板上的元素(x, y)映射的高斯值计算公式为:

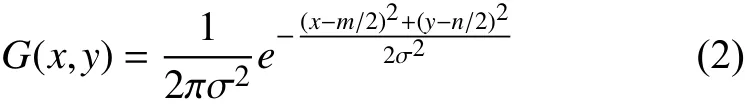
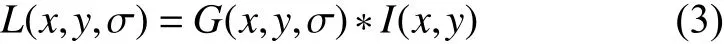
1.2 基于SIFT特征匹配的图像排序算法

针对自动排序存在的问题, 如待拼接的图像需要按顺序输入等, 研究人员提出了各种图像排序算法. 本文基于SIFT特征匹配引入一种新型图像排序算法[6]. 该算法可以实现图像排序, 并且不需要任何手动干预.

I1, I2分别代表两张图像. 首先依次提取I1和I2的SIFT特征, 然后进行特征匹配. 在理想条件下, 只要I1和I2有重叠区域, 便可以获取SIFT特征匹配点对. 如果没有, 则无法获取SIFT特征匹配点对. 根据这个分析, 本文引入一种基于SIFT特征匹配的图像排序的算法, 设有图像集, 集合R=NULL; 图像的SIFT特征点集, P是存储图像匹配点对集合的向量, P=NULL. 具体算法步骤如下:

1) 从集合S中随机选一张图片Im, 1≤m≤n

2) A=1

3) 如果IA属于R, 则令Im和IA的匹配点对集PA=NULL. 否则, 对Im和IA进行配准, 即对tm和tA进行SIFT特征匹配, 得到匹配点对集合PA; P=P+PA

4) A=A+1 如果A＞n, 转到步骤5, 否则转到步骤3

5) 计算集合P中Pi的元素个数di, 1≤i≤n, 得到

6) 找出集合D中的最大值dk, 1≤k≤n, Im的最佳匹配图像是Ik, 将Ik加入集合R中, 即R=R+Ik

7) 使m=k, 更新n的值, n=n-1

8) 如果n=1, 跳到步骤9, 否则跳到步骤2

9) R=R+(S-R), 算法终止

由以上算法输出的R即是图像集序列, 该集合中的图像在空间场景中有序排列, 能够直接用于全景图像拼接.

2 特征点匹配

SIFT算法虽具备旋转不变、光照不变、尺度不变等很多优势, 但该算法也存在如计算复杂度高、误匹配点较多等缺点, 影响了全景图像拼接的真实性, 本文在以下几点进行改进. 结合FAST算法依据高斯差分金字塔图像来实施特征点提取, 增强算法的运行效率, 针对相邻图像间的亮度差异, 采用图像亮度差异自动校正操作, 便于特征点匹配; 同时采用改进的RANSAC算法剔除误匹配点对, 实现更好的图像融合.

2.1 结合FAST算法提取特征点

特征点检测是图像拼接技术的第一步, 对整个算法执行效率起着关键的作用. 传统SIFT算法首先建立好高斯金字塔, 接着采取极值点检测、关键点定位等方法, 复杂度较强. 而FAST算法作为公认的快速特征点检测法, 通过计算某像素点和周围像素点的灰度差,从而出该像素点是不是极值点, 大大降低了复杂性, 提高了算法的执行效率.

文中在SIFT图像匹配技术中结合FAST算法, 最初随机选取某个像素点P, 接着构造半径为3的圆, 比较圆周上选取的16个像素点, 如果像素值中存在四分之三满足公式4, 即P被视为角点. 圆周上任一点的灰度值视为Ix, P点的灰度值即为Ip, 已知的阈值常数t. 式中: 满足界定前提的像素数量N, 当N超过给定阈值, 即P视为一个特征点.

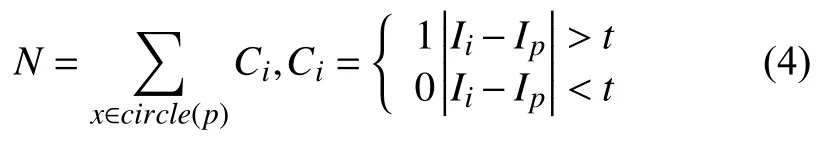
对现有高斯差分金字塔图像结合FAST算法特征提取的主要过程如下:

1) 计算中心的点P像素值与圆周边缘1到9编号的像素点存在的灰度差值, 判断两个值的绝对值大小是否超过给定阈值t, 如果都大于即P视为候选特征点, 继续下一步计算.

2) 进一步计算点P的像素值和圆周边缘上标有点5和点13像素点存在的灰度差值, 如果点1、9、5、13满足四分之三即至少三个点差值大于给定阈值t或小于它的相反数-t, 即该点视为候选特征点, 继续下一步计算.

3) 反复执行步骤1、2, 遵循准则检测完圆周边缘上16个像素点.

图2为FAST特征点检测的模板图.

图2 FAST特征点检测模板图

2.2 图像亮度差异自动校正

由于主观因素, 采集的原始图像会出现不同程度亮度差异, 故在特征点检测原始图像之前先进行图像亮度差异调整[7], 使得左右两幅图像亮度渐进一致, 从而获得更有效的特征点, 同时能改善拼接痕迹, 实现更好融合效果.

根据前面图像排序算法确定出的相邻图像的重叠区域, 通过重叠区域的像素均值削弱拍摄时带来的亮度差异, 过程如下:

分别计算两幅相邻图像重叠处的像素均值, 记为I1和I2, 即得到公共均值:

依据公共均值来调节I1和I2的亮度差异, 如下式所示:

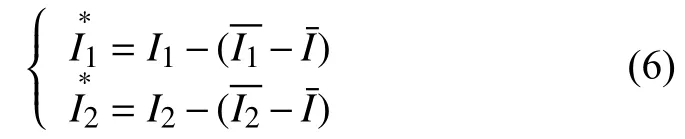
经调节后, 待拼接图像的亮度整体保持一致, 接着按照特征点检测与匹配操作, 实现高效提取角点、降低误匹配率、图像效果更清晰.

2.3 改进的Ransac算法剔除误匹配点对

特征点提取后, 即需确定相邻两幅图像之间特征点对应关系—特征点匹配. 本文通过归一化相关法(NCC)[8], 其相关系数理论如下:

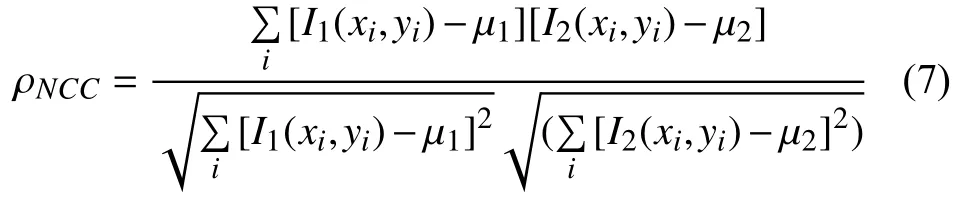
式中: μ1, μ2代表相关窗口的像素灰度平均值. 根据最大相关性双向搜索图像1、2, 当特征点彼此重合时, 即认为是一对匹配点, 通过该方法搜索直到所有的匹配点对被找到. 不难发现该算法获取的匹配点对存在部分“伪点对”, 需通过Ransac(随机一致性算法)对以上获取的匹配点对进行过滤, 提高匹配精确率.

传统的Ransac算法在外点较多时会构造错误模型,本文的Ransac算法在执行之前首先判断特征点的方向是否相同, 提升匹配点对的准确率; 同时运用临时模型预检测方法以提高算法的执行效率. Ransac算法的基本思想: 对象样本通常包含正常数据以及因种种原因生成的异常数据, 正确的模型通常由正常数据建立, 异常数据较此模型往往偏离较远, Ransac算法使用迭代方式估计数学模型参数以获取有效样本数, 本文实现算法步骤如下:

1) 计算所有匹配对中特征点方向差, 接着建立位于0到360间含有36个区的直方图, 即每个区为10°, 统计每区存在的匹配点对数量, 选取最大区匹配点对为候选匹配点对.

2) 依据以上得到的匹配点对中选取5对匹配点, 再从中随机选取4对线性估计变换矩阵H, 找到临时模型,继而检验另外一对是否在模型上, 如不在即放弃重选, 否则作为候选模型并继续寻找其支撑点集. 如公式(8)所示:

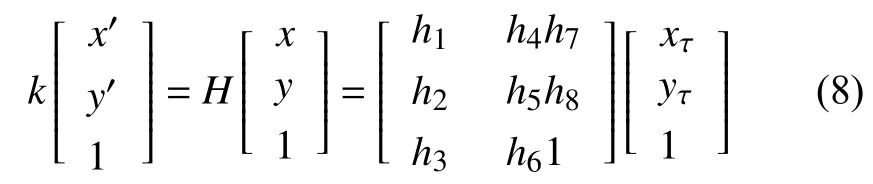
3) 计算所有匹配点对离H的垂直距离d, 依据d<阈值t判断所有匹配点对的内点对, 多次实验对比得出阈值取值越小越稳定, 当所有匹配点对中正确匹配点对数的比例不少于93%时, 即认为最佳匹配集合.

4) 重复以上步骤, 直到内点对集合最大, 记下H, 即为所求矩阵.

3 图像融合

通常图像有序拼接之后会存在明显缝隙, 因此还需做融合处理[9]. 本文采用加权平衡算法, 其主要理论:引入渐进因子, 范围在(0, 1)之间. 生成加权平均[10], 式(9): f11、f22、fw分别为基准图像、待匹配图像及融合后图像.

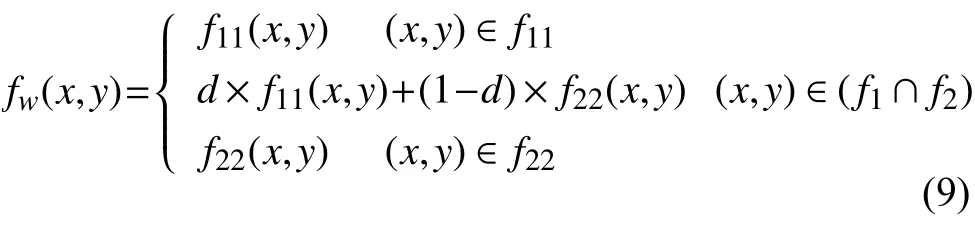
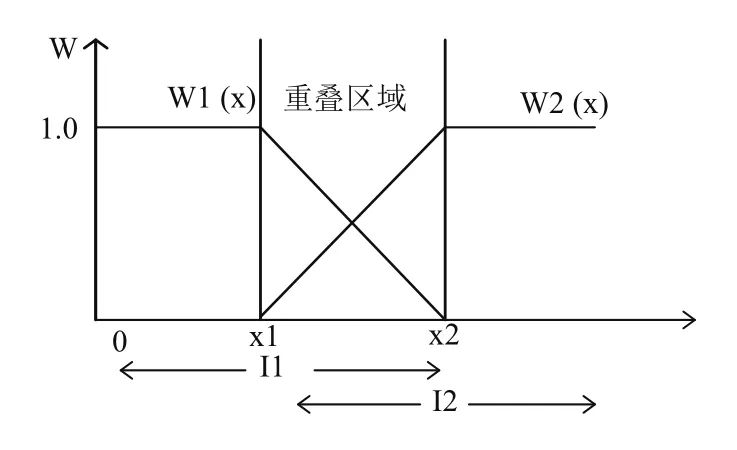
图3 权值计算方法

4.2 全景图像拼接实现

图4是6张无序图像, 这些图像从左至右、从上之下分别I1～I6.

图4 无序的图片

使用1.2节中基于SIFT特征匹配的图像排列算法,6张图像的计算结果如表1所示.

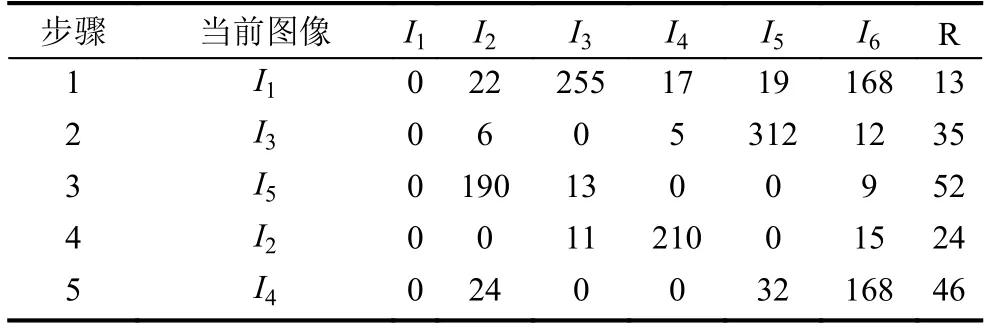
表1 基于SIFT特征图像排序算法过程

在表1中, 交叉点处数字表示两图像之间匹配点数量. 根据R中最后一列和最后一行结果, 可得到排序后图像, 实现了图像有序排列.

为了验证优化后算法的高效性, 随机选取排序后相邻两张图像进行实验, 其中两幅图像之间特征点的连线即一组匹配对, 如图5(a)和5(b)分别用于拼接的左右原始图像, 图6(a)和图6(b)则代表原始的SIFT算法和改进优化后算法通过特征点配准所得实验结果, 图6(c)和7(d)则为最后得到的两幅图像的拼接效果.

以上实验具体运行结果如表2所示, 每次实验数据为重复五次实验得到的数据均值.

4 实验结果及分析

4.1 实验说明

为了验证改进后算法的可行性, 实验环境硬件如

图5 拼接实验原始图

图6 原始算法和优化算法匹配效果

表2 正常实验下的拼接数据

从表2中的实验数据可以得出结论: 表2中算法改进前后完成匹配的时间分别是2.75 s和1.35 s, 效率进一步提升. 原因在于改进后的算法避免了原SIFT算法对每层高斯差分金字塔采取特征点提取造成的运算时间较长问题, 取而代之的是FAST检测算法相结合, 快速完成特征点检测, 进一步提高算法效率.

同时改进后的算法减少了误匹配率, 由之前SIFT算法正确匹配率的89%提升到93.9%, 获取到的匹配点对分别为52对和32对, 即改进后算法获取到的匹配点对数较少, 从图6(a)可以很明显的看到误匹配点对, 而图6(b)将误匹配点对进一步剔除; 原因在于Ransac算法在建立正确判断模型之前采取了特征点对方向特征的判断操作, 同时运用临时模型预检测思想, 从而剔除误匹配点对, 同时从图6(c)和图6(d)对比可看出改进后算法因减少了误匹配点对, 从而避免对应图像关系错位,即拼接图像无明显条纹、褶皱, 拼接效果更真实.

依据改进后的算法进行特征点匹配后, 进一步根据加权平衡算法实现图像的快速融合, 最终实现图像的全景拼接, 效果图如图7.

图7 最终拼接全景图

5 结论

针对全景图像拼接在实际应用中存在的复杂性和误匹配点对较多问题, 本文引入一种新型的基于SIFT特征提取的全景图像自动排序算法, 实现了图像全景拼接, 充分体现了该算法的自动性和适用性. 结合高效的FAST算法获取高斯金字塔图像中特征点对, 从而提升算法运行效率; 在特征点提取之前先调节图像的亮度差异, 保证图像视觉的一致性, 体现了图像的真实性,同时通过改进的RANSAC算法剔除了大量误匹配点对,提升了算法的精确度. 最终根据加权平衡算法实现图像的快速融合. 实验表明, 本文的算法优化在清晰度、准确度、效率和自动化程度方面均有较大提高.

1侯舒维, 郭宝龙. 一种图像自动拼接的快速算法. 计算机工程, 2005, 31(15): 70–72.

2杨占龙, 郭宝龙. 基于兴趣点伪泽尼克矩的图像拼接. 中国激光, 2007, 34(11): 1548–1552.

3张朝伟, 周焰, 吴思励, 等. 基于SIFT特征匹配的监控图像自动拼接. 计算机应用, 2008, 28(1): 191–194.

4常青, 张斌, 邵金玲. 基于SIFT和RANSAC的特征图像匹配方法. 华东理工大学学报(自然科学版), 2012, 38(6): 747–751.

5闫志, 王黎明, 陈平. 基于多目标优化的SIFT特征匹配算法. 现代电子技术, 2010, 33(12): 99–102.

6李晓娟. 图像拼接技术研究[硕士学位论文]. 西安: 西安电子科技大学, 2007.

7王蕾. 图像配准技术及应用研究[硕士学位论文]. 西安: 西安电子科技大学, 2007.

8Xu PF, Zhang L, Yang KY, et al. Nested-SIFT for efficient image matching and retrieval. IEEE MultiMedia, 2013,20(3): 34–36. [doi: 10.1109/MMUL.2013.18]

9Zhao WJ, Gong SR, Liu Q, et al. An Auto-sorting arithmetic for image sequence used in image mosaics. Journal of Image and Graphics, 2007, 12(10): 1861–1864.

10Lowe DG. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 2004,60(2): 91–110. [doi: 10.1023/B:VISI.0000029664.99615.94]

Research on Panoramic Image Mosaic Technology Based on SIFT Algorithm

WEN Wei-Dong, ZHANG Ming
(Information Engineering College, Shanghai Maritime University, Shanghai 201306, China)

Panoramic image mosaic technology is a 360-degree circular image that combines the images of some overlapping areas to describe a particular scene. In this paper, a novel image sorting algorithm based on SIFT (Scale Invariant Feature Transform) feature matching is proposed to achieve the orderly arrangement of images. Aiming at the problem that the image mosaic has many mismatch points and takes a long time,the FAST algorithm is used to extract feature points. And then, an auto-correcting operation is adopted for the brightness difference between the adjacent ordered images to reduce the brightness difference, and the modified Ransac algorithm is used to eliminate the mismatching points. Finally, the Weighted Equalization Algorithm is used to realize the Fast fusion of the image. The experimental results show that the algorithm is stable and efficient.

panoramic image stitching; image sorting; automatic calibration; weighted balance; fusion

文伟东,张明.基于SIFT算法的全景图像拼接技术研究.计算机系统应用,2017,26(7):227–231. http://www.c-s-a.org.cn/1003-3254/5899.html

2016-11-20; 收到修改稿时间: 2017-01-16