基于A*算法的三维地图最优路径规划①

赵德群, 段建英, 陈鹏宇, 苏晋海

(北京工业大学 信息学部, 北京 100124)

基于A*算法的三维地图最优路径规划①

赵德群, 段建英, 陈鹏宇, 苏晋海

(北京工业大学 信息学部, 北京 100124)

研究了基于A*算法的适合人步行行走的山地环境下三维地图最优路径规划算法及实现. 本文考虑了三维山地无路网信息覆盖的条件较差环境, 对A*算法进行改进, 并利用三维地形DEM数据计算出一条相对平缓且长度较短的三维路径. 改进算法对三维条件下路径最短的评价标准由原有的空间距离累加最短改进为先将空间等效成水平距离, 再计算距离是否最短. 同时, 本文充分考虑了搜索点周围环境的整体坡度信息作为启发信息, 来降低算法寻找的路径走在陡坡上的概率. 实验表明, 本算法最终计算出的三维最优路径在平缓度及路径最短上有所改善, 基本符合人步行行走的习惯.

A*算法; 三维地图; 山地; 最优路径规划; DEM

传统地图服务已经成为人们每天外出必须的功能,其无论是形式还是技术发展都较为成熟, 在实际中得到了广泛应用[1]. 其中, 路径规划在交通导航这个方向上应用广泛, 极大地方便了人们的外出. 然而, 现有的各大路径规划系统全部是在二维地图平台上实现, 并且严重依赖于交通路网这些数据[2], 同时这些路网信息几乎全部集中于大中城市, 对于乡镇以及山地等偏远地区几乎找不到路网信息. 通过路网信息的辅助, 可以很容易的规划处一条最优的路径, 但在没有路网的条件下现在的路径规划算法却毫无办法.

在二维路网式路径规划给人们带来便利的同时,人们对路径规划的要求也有所提高, 由二维转向三维、由有路网转向无路网, 例如森林救火的行进路线自动规划、戈壁滩的行车路径规划问题, 规划出结果的同时能在三维地图上有更为直观的展示.

对于三维路径规划问题, 目前主要的算法有蚁群算法、遗传算法、粒子群算法、人工势能算法、A*算法等. 文献[3-5]分别对蚁群算法进行了改进并应用到三维路径规划问题中, 取得了一定效果, 但是蚁群算法收敛速度慢、容易陷入局部最优解的问题没有得到有效解决; 文献[6]利用遗传算法提出了一种针对于AUV海底三维路径规划的解决方案, 对AUV的安全航行起到了重要的参考价值, 但算法容易出现早熟及稳定性较差; 文献[7,8]针对于飞行器飞行安全问题提出了基于粒子群算法的三维路径规划算法, 简化了模型及参数调整的步骤, 提升了飞行器飞行的有效性, 同时该算法也出现了搜索过程过早结束难以找到最优解的问题.

文献[9]将启发函数与人工势场法相结合进行了仿真, 仿真结果可以避开障碍物同时进行了平滑处理, 但是算法得出的结果是否最优难以确定. 文献[10-14]分别利用A*算法并进行改进, 在二维网格或者游戏地图型中进行仿真, 得出较为满意的路径, 为三维路径规划问题提供了参考, 但是以上算法大多采用简单的二维或三维仿真模型进行试验, 数据量和复杂程度都远远低于真实地形地图, 不具备一定的实用性.

本文针对于山地没有路网覆盖的情形, 利用A*算法并在考虑三维地形坡度问题的基础上对原有算法进行改进和优化, 得出一条位于三维地图两点之间的坡度符合人步行行进且路径最短的最优路径, 同时在三维实景地图展示最后的规划路径结果, 满足了人的视觉需求, 具有一定的实用性.

1 研究目标

本文致力于研究出一种针对于山地, 适合人步行前进的坡度平缓且路径长度最短的路径. 本文采用三维地图模型进行实验以更加接近人在山区行进的真实环境. 在给定实验区域任意两点的情况下, 能够实时计算出适合人行走的路径, 同时显示在三维实景地图上. 三维实景地图的最优路径规划问题可以直观地表示为图1.

2 三维路径规划算法实现

2.1 数据准备

三维地图山地最优路径规划的问题实质上就是将一个已知的三维实景地图模型进行栅格化处理, 利用DEM(高程模型)数据将一个三维地图降维成二维栅格地图进而利用二维栅格中存储的数据进行计算得出最优路径的问题.

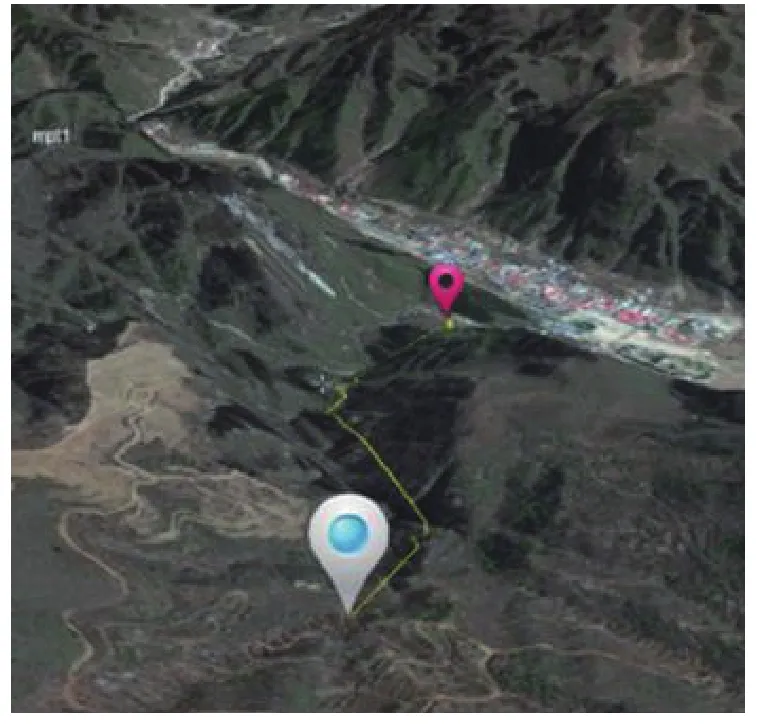
图1 三维路径规划

本文实验所用的DEM数据由测绘无人机进行航飞并通过后期数据处理得到grd格式的存储文件. 本文程序运行前需要预处理将grd文件里存储的DEM数据解析、读出并存储到特定形式的数据结构中.

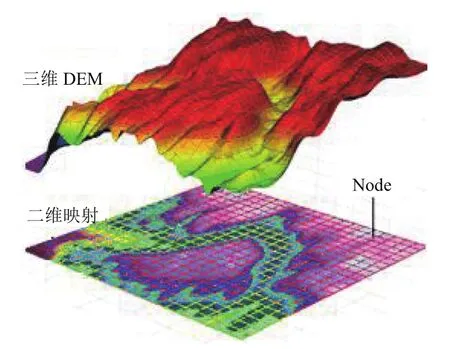
图2 DEM数据映射图

如图2所示, 本文将一片DEM数据转化为图示下方的二维映射, 其中DEM数据集合可表示为:

其中D为DEM数据集合, Xmin表示整片区域最小经度,Xmax表示最大经度, Ymin表示最小纬度, Ymax表示最大纬度, NumCol表示DEM数据的总列数, NumRow表示DEM的总行数.

二维映射可以表示为一个由NumCol*NumRow个Node节点的二维数组: Data[NumCol][NumRow].

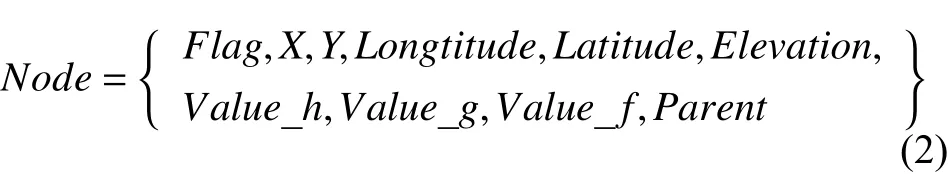
● Flag——节点标识;

● X——节点所处二维数组的横坐标;

● Y——节点所处二维数据的总坐标;

● Longtitude——节点经度;

● Latitude——节点纬度;

● Elevation——节点高程;

● Value_h——节点到终点的启发值;

● Value_g——节点到起点走过的实际值;

● Value_f——Value_h与Value_g的和;

● Parent——节点的父节点.

上式中节点标识Flag可以表示为:

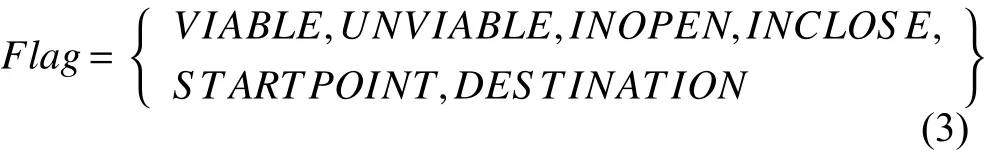
● VIABLE——节点可以通行;

● UNVIABLE——节点不适合通行;

● INOPEN——节点在开放列表(开放列表将在下节阐述)中;

● INCLOSE——节点在关闭列表(关闭列表将在下节阐述)中;

● STARTPOINT——节点为起始节点;

● DESTINATION——节点为终止节点.

2.2 基本算法介绍

A* 算法引入了估值函数: , G(i)是栅格i到起始栅格的已知最短距离, 称为代价函数;H(i)是栅格i到目标栅格的估计值[8], 称为启发函数.

如果H(i)总是小于或等于从i到目标的实际花费,那么A*算法就能确保找到最短路径, H(i)的值越小,A*算法要扩展的节点就越多, 算法就越慢[13]. 对于三维A*算法通常H(i)取欧几里德距离作为启发值, 由于这个启发值通常小于栅格i和终点栅格e的实际距离, 因此能够保证搜索的路径距离最短, 例如文献[9]和文献[14]皆用到了欧几里德距离作为启发值. 启发值H(i)取栅格i和终点栅格e之间的三维距离, 计算公式:

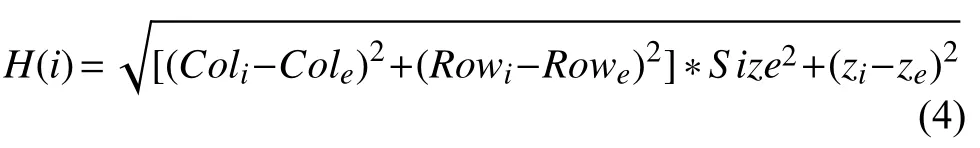
其中(Rowi, Coli)为栅格i的行列号, zi为栅格i的高程,Size为栅格的分辨率. G(i)为栅格i到起始栅格s的已知最短距离, 其计算公式为:

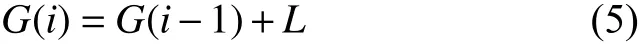
其中 为栅格i的父栅格i-1到起始栅格s的累积最短距离, L为栅格i到其父栅格i-1的距离, 在通常情况下L取的是两点之间的三维空间直线距离. 对于上述算法,本文称之为3DBA*算法.

3DBA*算法理论上能够搜索到一条最短的路径,比较适合于二维地图和较为简单的规则三维游戏地图模型. 经过实验本文发现由真实DEM数据表示的山地区域来说, 地形较为复杂, 而3DBA*算法只考虑最短距离却没考虑坡度问题, 因此不能完全适用. 如图3方框内的路线所示, 3DBA*算法计算出来的路径往往走在陡峭的山坡上, 这样的路径过于危险, 并不适合人的行走. 因此, 在3DBA*算法的基础上, 本文从距离最短和坡度较缓两方面因素入手提出一种改进型A*算法, 适合于三维山地地形, 适合于人行走同时路径较短, 本文称之为3DA*算法. 本文将在下一节详细描述3DA*算法的实现方法.

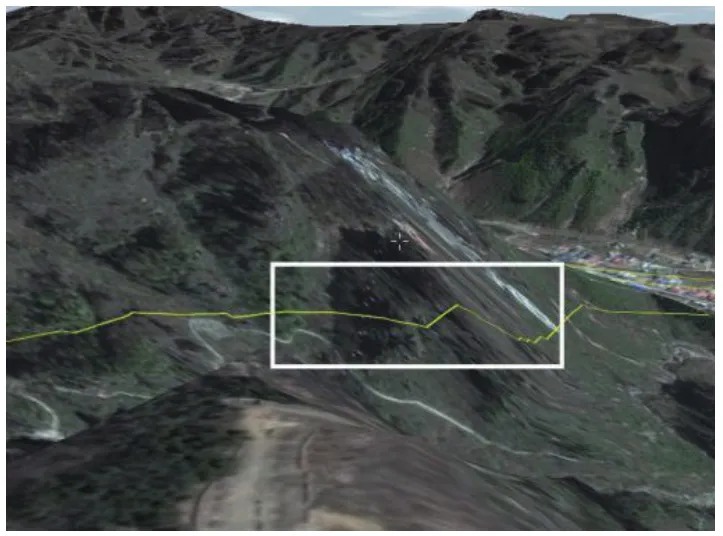
图3 3DBA*算法危险路径

2.3 改进算法(3DA*)的实现

2.3.1 坡面与水平地面距离的等效

文献[15]中Chyi-Rong等人兼顾坡度及体能消耗等多种因素并在多处山地环境下进行亲身测试得出人在山地步行行走的速度与坡度的关系如下所示:

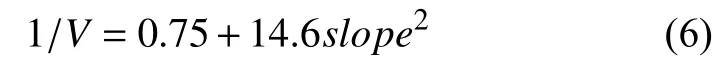
式中V为人的步行速度, slope为地形坡度的正切值

由式(6)可以推出: V0=4/3(坡度为0时速度)

由式(6)和V0=4/3可以推出在坡度为slope的山地上行走单位距离S与等效水平地面距离S0的比值为:

由式(6)可以看出, 在坡上行走的速度随坡度增大减小, 坡度增大的同时也会增加体能的消耗[10]. 再由式(7)可以发现利用式(5)所表达的空间距离评价已走路径是否为最短并不科学, 因为在坡面上行走单位距离并不等于相同的水平距离, 在坡面上行走较为困难, 实际等效成的水平距离要大于相对应的坡面距离. 本文提出, 评价路径最短的标准可以将式(5)坡面上行走的坡面距离由式(7)先等效成水平距离, 再判断距离是否最短.

2.3.2 改进算法描述

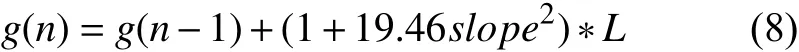
式(8)只是在考虑了坡度影响人行走速度的情况下提出的新的评价山地地形最短路径的标准, 一定程度上影响了算法寻找出的路径, 使路径坡度总体变缓, 但是实验结果发现在不改变2.2节所述3DBA*算法启发函数h(n)的情况下, 算法寻找出的路径仍然存在2.2节提出的路径走在陡坡上的问题. 因此本文对启发函数h(n)进行了改进:

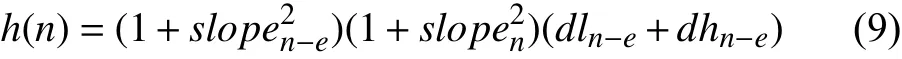
式(9)中n代表当前被遍历的地图节点, e代表终点节点,图4中Center代表当前正在处理的节点, Center的周围节点(图4中A～H节点)代表待遍历的节点. 式(9)中其他符号表示如下所述.

图4 处理节点Center与遍历节点A-F

dln-e表示A～H中的被遍历到的节点n与终点e的水平距离; dln-e表示A～H中的被遍历到的节点n与终点e的高度差值;表示A～H中的被遍历到的节点n与终点e的坡度正切值表示A～H中的被遍历到的节点n与当前处理节点Center的坡度正切值(如).

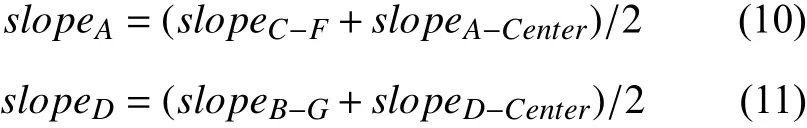
需要注意的是如果式slopen的值大于0.35时, 本文将此节点的Flag置为UNVIABLE.

2.3.3 实现步骤

算法需要建立两个列表来存储节点数据, 一个为“开启列表”, 本文称之为OpenList, 用来存储等待检查的节点; 另一个为“关闭列表”, 本文称之为CloseList, 用来存储不需要再次检查的节点.

以下为算法的流程:

1) 首先初始化式(2)中存放Node节点数据的二维数组, 初始化过程中将每个Node分别根据DEM数据计算出每个Node对应的数组坐标、经纬度、高度等信息, 需要说明的是如果当前初始化的节点是起点(Start Point)则此Node的Flag赋值为式(3)中的STARTPOINT,如果当前初始化节点是终点(EndPoint)则此Node的Flag赋值为式(3)中的DESTINATION, 其他的节点Flag一律初始化为式(3)中的VIABLE. 从StartPoint开始执行, 并当做当前需要处理的节点存入OpenList.

2) 从OpenList中取f(n)值最小的节点(如果OpenList中只有起点则为StartPoint)作为当前待处理的节点如图4所示Center. 遍历Center节点周围可以到达的8个节点(图4中A～H), 如果发现这8个节点内已经出现Flag为DESTINATION的节点, 终点找到, 退出路径搜索, 执行步骤8.

3) 当前被遍历到的8个节点中的某个节点本文称之为NewPoint, 如果NewPoint的通行状态Flag为UNVIABLE或INCLOSE, 则代表此节点地形无法通过或这个节点已经被存放于CloseList中, 跳过此节点, 继续遍历下一点; 否则, 执行下一步. 如果周围8个节点遍历完毕, 执行步骤7.

4) 如果NewPoint的Flag为VIABLE, 节点可通行,则将它放入“开启列表” OpenList, Flag置为INOPEN, 同时将其 “父节点”置为Center, 然后执行步骤5; 如果NewPoint已经在开启列表中, 跳过步骤5, 执行步骤6.

5) 如果式(10)或式(11)计算出NewPoint的slopen的值大于0.35, 将此节点的Flag置为不可通行状态UNVIABLE, 否则计算NewPoint的g(n)和h(n)以及f(n),之后, 将NewPoint存入OpenList, 并且OpenList中的节点总是按f(n)的值升序排列, 执行完毕, 返回步骤3遍历下一个节点.

6) 当NewPoint已经在开启列表中时, 计算此NewPoint相对于中心节点Center的g(n)值, 如果新计算的g(n)小于之前存储的g(n)值, 则将此节点的g(n)值更新为新计算的值, 并将此节点的父节点更改为当前的中心节点Center, 否则, 本文将什么都不做, 返回步骤3遍历下一个节点.

7) 将OpenList的第一个节点(f(n)最小的节点)移入CloseList, 返回2继续执行直到找到终点为止.

8) 由终点Node开始根据Parent节点往前追溯, 直到追溯到Parent为null的起点, 得出出一条存储路径的链表, 寻路过程结束.

3 实验

本文利用一片大致10 km*10 km, 节点间隔5 m的DEM数据, 进行了大约50组实验, 每一组实验分别记录了3DBA*算法与改进算法3DA*算法的路径长度、平均坡度、算法计算时间以及实验结果的效果图.

需要说明的是本文记录的路径长度是将利用式(7)将空间距离根据坡度信息等效成水平距离后得出的数据, 最终本文评价所得路径长度的标准为:

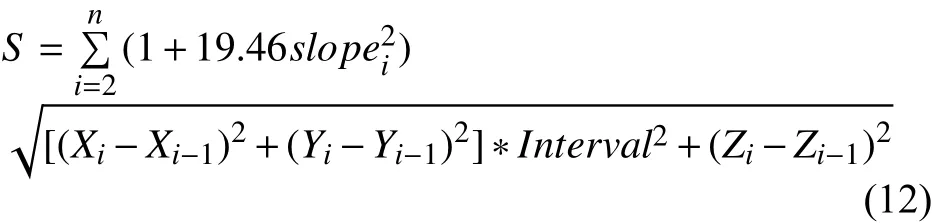
其中slopei为节点i与节点i-1之间的坡度正切值, Interval在本实验中如果不在图4对角节点时为5 m, 否则乘1.4为7 m.

本文记录的路径平均坡度就是计算得出的轨迹点串相邻点的坡度正切值累加和再除以点数取均值得出的数据, 本文评价所得路径坡度的标准为:

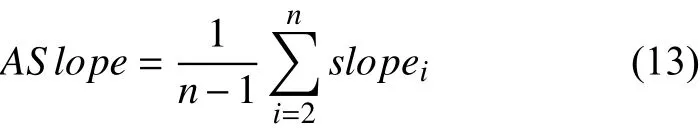
本文记录的算法计算时间即从开始搜素到搜索结束找到终点程序运行的时间.

3.1 实验效果分析

实验的效果图如图5所示, 点线代表原始3DBA*算法结果, 实线代表本文改进的3DA*算法, 图下方定位点代表起点, 图上方定位点代表终点. 本文从实验结果中任意截取了两幅上坡的路径(a)(b)与两组下坡的路径图(c)(d), 效果图如图5所示.

图5 实验效果图

从实验结果效果图直观分析, 3DBA*的点线路径大多没有顾及到山坡的陡峭性, 本文的算法所得出的实线路径相对较为平缓, 且基本避开了较为陡峭的山坡转而寻找较为平缓且距离相对最近的路.

3.2 实验数据分析

本文根据实验所得的50组结果数据进行统计, 将最终的结果分别按路径从小到大的进行显示, 并用EXCEL软件做出数据走向的趋势.

(1) 算法所得路径长度

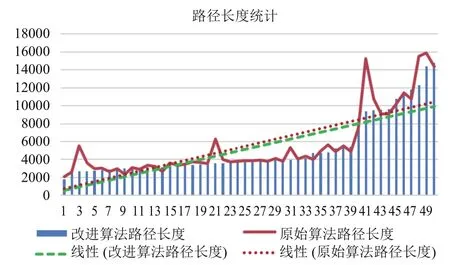
图6 路径长度统计

由图6可以看出, 实体曲线代表的原始算法计算出的等效水平路径长度几乎总是在改进算法路劲长度的上方, 从虚线代表的各自趋势线也可以看出, 两种算法最终算出的路径长度几乎相等, 但总的趋势是改进算法稍优一点.

(2)算法所得路径平均坡度

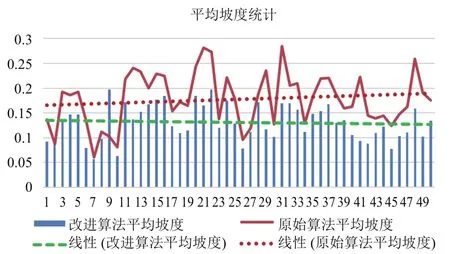
图7 平均坡度统计

由图7可以看出, 原始算法的平均坡度除极少数情况小于改进算法, 其他绝大部分情况明显大于改进算法的平均坡度, 由此也可以说明本算法寻找出的路径明显要平缓很多, 更适合人行走的要求.

(3) 算法搜索时间

图8 算法时间统计

从图8统计数据来观察, 两种算法的计算时间有大有小, 很难分清哪种算法用的时间少. 但是, 由于本文将数据根据路径长度由小到大的顺序重新进行了统计,本文通过EXCEL软件做出的虚线代表的趋势线可以看出, 改进算法在范围较小的区域内搜索路径时, 搜索时间大于原始算法的搜索时间, 但随着搜索范围的增大,本文的改进算法搜索的时间有小于原始算法搜索时间的趋势. 此外, 从数据上看, 本算法寻找路径的范围在方圆10公里左右, 在这个范围内算法所用的时间基本上小于1200 ms, 在这样复杂的地形环境下, 算法时间基本可以忍受.

4 总结

本文着眼于三维实景地图, 并针对于地形较为复杂的山地, 在传统A*最优路径搜索算法的基础上, 经过改进得出一种适合于山地行走的最优路径搜索算法.本改进算法通过将有坡度的路径空间距离等效为水平距离重新定义了评价路径长短的标准, 并通过此标准记录算法实际走过的路程, 与此同时本文充分考虑了搜索点周围环境的整体坡度信息作为启发信息, 来降低算法寻找的路径走在陡坡上的概率. 通过实验可以看出, 本文的改进算法较之基础算法, 整体坡度更为平缓, 等效为水平路径的长度比基础算法稍短, 算法运算时间随着搜索范围的增大有小于基础算法的趋势. 综合以上内容, 本文可以得出结论: 本文的算法在针对山地这一类地势较为复杂的三维地形时能够搜索出一条坡度适于人行走, 距离较短的路径, 且在方圆10公里这样的范围内搜索时间对于人来说能够接受.

1张栋海, 韩丽华, 肖雄兵, 等. 导航地图发展现状和趋势分析. 地理信息世界, 2013, 20(2): 20–23, 36.

2王俊. 面向智能交通的路径规划相关技术研究[硕士学位论文]. 南京: 南京大学, 2013.

3王弋. 基于高程环境与蚁群算法的三维路径规划研究[硕士学位论文]. 西安: 西安工业大学, 2014.

4黄玲, 胡蔚蔚. 基于改进蚁群算法的果蔬采摘机器人三维路径规划. 农机化研究, 2016, (9): 38–42.

5黄劲潮. 一种基于改进蚁群算法的山地三维路径规划算法. 荆楚理工学院学报, 2014, 29(2): 40–44.

6郝燕玲, 张京娟. 基于遗传算法的AUV三维海底路径规划.中国工程科学, 2003, 5(11): 56–60. [doi: 10.3969/j.issn.1009-1742.2003.11.008]

7张航, 刘梓溪. 基于量子行为粒子群算法的微型飞行器三维路径规划. 中南大学学报(自然科学版), 2013, 44(S2): 58–62.

8李挚, 宋顶立, 张双江, 等. 两种改进的最优路径规划算法.北京科技大学学报, 2005, 27(3): 367–370.

9陈春梅. 无人机快速三维航迹规划算法的研究[硕士学位论文]. 成都: 电子科技大学, 2015.

10王鹏程, 夏洁. 基于特殊双向A*搜索算法的三维航迹规划.系统仿真学报, 2009, 20(增刊): 229–233.

11邱磊. 利用跳点搜索算法加速A*寻路. 兰州理工大学学报,2015, 41(3): 102–107.

12祁悦, 赵洋, 杨帆. 一种基于A*算法的分层路径规划在3D游戏中的应用研究. 电子设计工程, 2014, 22(14): 37–39,42. [doi: 10.3969/j.issn.1674-6236.2014.14.012]

13崔振兴, 顾治华. 基于A*算法的游戏地图最短路径搜索.软件导刊, 2007, (17): 145–147.

14石俊卫, 包世泰, 冯煜. 基于A*算法的山地最优路径分析.现代计算机, 2013, (14): 9–11, 15.

15Chiou CR, Tsai WL, Leung YF. A GIS-dynamic segmentation approach to planning travel routes on forest trail networks in Central Taiwan. Landscape and Urban Planning, 2010, 97(4): 221–228. [doi: 10.1016/j.landurbplan.2010.06.004]

Optimal Path Planning for 3D Map Based on A*Algorithm

ZHAO De-Qun, DUAN Jian-Ying, CHEN Peng-Yu, SU Jin-Hai
(Beijing University of Technology, Department of Information, Beijing 100124, China)

The optimal path planning algorithm and implementation of 3D map based on A * algorithm in mountainous environment are studied in this paper. It considers the condition of poor coverage of 3D mountain-free network information coverage, improves the A * algorithm and uses 3D terrain DEM data to calculate a relatively smooth and short three-dimensional path. The improved algorithm can improve the shortest path evaluation criterion in threedimensional space from the original spatial distance accumulation to the shortest distance, and then calculates whether the distance is the shortest. At the same time, the global gradient information of the surroundings of the search point is considered as the heuristic information to reduce the probability that the path the algorithm looks for is steep.Experimental results show that the proposed algorithm can improve the smoothness and shortest path of the threedimensional optimal path, which accords with the walking habits of human beings.

A * algorithm; three-dimensional map; mountain; optimal path planning; DEM

赵德群,段建英,陈鹏宇,苏晋海.基于A*算法的三维地图最优路径规划.计算机系统应用,2017,26(7):146–152. http://www.c-sa.org.cn/1003-3254/5859.html

国家重大科研仪器设备研制专项(1L001790201501)

2016-11-02; 收到修改稿时间: 2016-12-08